Mencapai strategi ekuiti yang seimbang dengan penyelarasan yang teratur

Mencapai strategi ekuiti yang seimbang dengan penyelarasan yang teratur

Dalam artikel sebelumnya (https://www.fmz.com/bbs-topic/9862), kami memperkenalkan strategi perdagangan pasangan dan menunjukkan bagaimana untuk membuat dan mengotomatiskan strategi perdagangan dengan menggunakan data dan analisis matematik.

Strategi ekuiti yang seimbang kedudukan pendek panjang adalah lanjutan semulajadi strategi perdagangan pasangan yang boleh digunakan untuk bakul objek dagangan. Ia sangat sesuai untuk pasaran dagangan dengan banyak jenis dan hubungan antara, seperti pasaran mata wang digital dan pasaran niaga hadapan komoditi.

Prinsip asas

Strategi ekuiti seimbang kedudukan pendek panjang adalah untuk pergi panjang dan pergi pendek sekotak sasaran dagangan pada masa yang sama. Sama seperti perdagangan pasangan, ia menentukan sasaran pelaburan mana yang murah dan sasaran pelaburan mana yang mahal. Perbezaannya adalah bahawa strategi ekuiti seimbang kedudukan pendek panjang akan mengatur semua sasaran pelaburan dalam kumpulan pemilihan saham untuk menentukan sasaran pelaburan mana yang relatif murah atau mahal. Kemudian, ia akan pergi panjang n sasaran pelaburan atas berdasarkan kedudukan, dan pergi pendek n sasaran pelaburan bawah dalam jumlah yang sama (jumlah nilai kedudukan panjang = jumlah nilai kedudukan pendek).

Adakah anda ingat apa yang kami katakan bahawa perdagangan pasangan adalah strategi neutral pasaran? Begitu juga untuk strategi ekuiti seimbang kedudukan pendek panjang, kerana jumlah kedudukan panjang dan pendek yang sama memastikan bahawa strategi akan kekal neutral pasaran (tidak dipengaruhi oleh turun naik pasaran). Strategi ini juga kukuh secara statistik; Dengan memberi peringkat sasaran pelaburan dan memegang kedudukan panjang, anda boleh membuka kedudukan pada model kedudukan anda berkali-kali, bukan hanya satu kali risiko kedudukan pembukaan. Anda semata-mata bertaruh pada kualiti skim kedudukan anda.

Apakah skim kedudukan?

Skema kedudukan adalah model yang boleh menetapkan keutamaan kepada setiap subjek pelaburan mengikut prestasi yang dijangkakan. Faktor-faktor boleh menjadi faktor nilai, penunjuk teknikal, model penetapan harga atau gabungan semua faktor di atas. Sebagai contoh, anda boleh menggunakan penunjuk momentum untuk memberi kedudukan kepada satu siri sasaran pelaburan pengesanan trend: diharapkan bahawa sasaran pelaburan dengan momentum tertinggi akan terus berprestasi baik dan mendapat kedudukan tertinggi; Objek pelaburan dengan momentum paling sedikit mempunyai prestasi terburuk dan pulangan terendah.

Kejayaan strategi ini hampir sepenuhnya bergantung kepada skim kedudukan yang digunakan, iaitu skim kedudukan anda boleh memisahkan sasaran pelaburan prestasi tinggi dari sasaran pelaburan prestasi rendah, supaya dapat lebih mewujudkan pulangan strategi sasaran pelaburan kedudukan panjang dan pendek.

Bagaimana untuk membuat skim kedudukan?

Apabila kita telah menentukan skim kedudukan, kita berharap untuk membuat keuntungan daripadanya. Kami melakukan ini dengan melabur jumlah modal yang sama untuk pergi panjang sasaran pelaburan atas dan pergi pendek sasaran pelaburan bawah. Ini memastikan bahawa strategi hanya akan membuat keuntungan berbanding dengan kualiti kedudukan, dan ia akan menjadi market neutral.

Misalkan anda memberi kedudukan kepada semua sasaran pelaburan m, dan anda mempunyai n dolar untuk pelaburan, dan anda ingin memegang jumlah 2p (di mana m>2p) kedudukan. Jika objek pelaburan kedudukan 1 dijangka melakukan yang paling teruk, objek pelaburan kedudukan m dijangka melakukan yang terbaik:

• Anda mengelaskan objek pelaburan sebagai: 1,...,p kedudukan, pergi pendek sasaran pelaburan 2/2p USD.

• Anda menilai objek pelaburan sebagai: m-p,...,m kedudukan, pergi panjang sasaran pelaburan n/2p USD.

Nota: Kerana harga subjek pelaburan yang disebabkan oleh turun naik harga tidak akan selalu membahagikan n / 2p secara merata, dan beberapa subjek pelaburan mesti dibeli dengan bilangan bulat, akan ada beberapa algoritma yang tidak tepat, yang harus sedekat mungkin dengan nombor ini.

n/2p = 100000/1000 = 100

Ini akan menyebabkan masalah besar untuk skor dengan harga lebih besar daripada 100 (seperti pasaran niaga hadapan komoditi), kerana anda tidak boleh membuka kedudukan dengan harga pecahan (masalah ini tidak wujud di pasaran mata wang digital).

Mari kita ambil contoh hipotetis.

• Membina persekitaran penyelidikan kami di atas platform FMZ Quant

Pertama sekali, untuk bekerja dengan lancar, kita perlu membina persekitaran penyelidikan kita.FMZ.COM) untuk membina persekitaran penyelidikan kami, terutamanya untuk menggunakan antara muka API yang mudah dan pantas dan sistem Docker yang dikemas dengan baik platform ini kemudian.

Dalam nama rasmi platform FMZ Quant, sistem Docker ini dipanggil sistem Docker.

Sila rujuk artikel saya sebelum ini mengenai cara menggunakan docker dan robot:https://www.fmz.com/bbs-topic/9864.

Pembaca yang ingin membeli pelayan pengkomputeran awan mereka sendiri untuk menggunakan pelabuhan boleh merujuk artikel ini:https://www.fmz.com/digest-topic/5711.

Selepas menyebarkan pelayan pengkomputeran awan dan sistem docker dengan berjaya, seterusnya kita akan memasang artifak terbesar sekarang Python: Anaconda

Untuk merealisasikan semua persekitaran program yang relevan (bibliotek ketergantungan, pengurusan versi, dan lain-lain) yang diperlukan dalam artikel ini, cara yang paling mudah adalah menggunakan Anaconda.

Untuk kaedah pemasangan Anaconda, sila rujuk panduan rasmi Anaconda:https://www.anaconda.com/distribution/.

Artikel ini juga akan menggunakan numpy dan panda, dua perpustakaan popular dan penting dalam pengkomputeran saintifik Python.

Kerja asas di atas juga boleh merujuk kepada artikel saya sebelumnya, yang memperkenalkan cara menyediakan persekitaran Anaconda dan perpustakaan numpy dan panda.https://www.fmz.com/digest-topic/9863.

Kita menghasilkan sasaran pelaburan rawak dan faktor rawak untuk memberi kedudukan kepada mereka. mari kita anggap bahawa pulangan masa depan kita sebenarnya bergantung kepada nilai faktor ini.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

Sekarang kita mempunyai nilai faktor dan pulangan, kita boleh melihat apa yang berlaku jika kita peringkat sasaran pelaburan berdasarkan nilai faktor dan kemudian membuka kedudukan panjang dan pendek.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

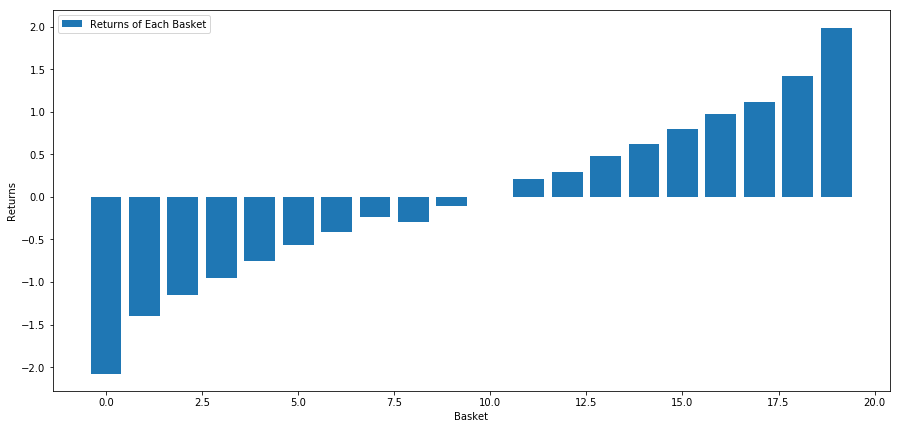
Strategi kami adalah untuk pergi panjang keranjang peringkat pertama kumpulan sasaran pelaburan; pergi pendek daripada keranjang peringkat kesepuluh. pulangan untuk strategi ini adalah:

basket_returns[number_of_baskets-1] - basket_returns[0]

Hasilnya ialah: 4.172

Letakkan wang pada model ranking kami supaya ia dapat memisahkan sasaran pelaburan berprestasi tinggi dari sasaran pelaburan berprestasi rendah.

Dalam artikel ini, kita akan membincangkan bagaimana untuk menilai skim kedudukan. Kelebihan pertaruhan berasaskan kedudukan adalah bahawa ia tidak dipengaruhi oleh gangguan pasaran, sebaliknya gangguan pasaran boleh digunakan.

Mari kita pertimbangkan contoh dunia sebenar.

Kami memuatkan data untuk 32 saham dalam industri yang berbeza dalam indeks S&P 500 dan cuba memberi kedudukan kepada mereka.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Mari kita gunakan penunjuk momentum standard untuk tempoh satu bulan sebagai asas untuk kedudukan.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Sekarang kita akan menganalisis tingkah laku saham kita dan melihat bagaimana saham kita beroperasi di pasaran dalam faktor kedudukan yang kita pilih.

Menganalisis data

Tingkah laku stok

Mari kita lihat bagaimana keranjang saham yang dipilih kami berprestasi dalam model kedudukan kami. Untuk melakukan ini, mari kita mengira pulangan hadapan mingguan untuk semua saham. Kemudian kita dapat melihat korelasi antara pulangan hadapan 1 minggu setiap saham dan momentum 30 hari sebelumnya. Saham yang menunjukkan korelasi positif adalah pengikut trend, sementara saham yang menunjukkan korelasi negatif adalah pembalikan purata.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

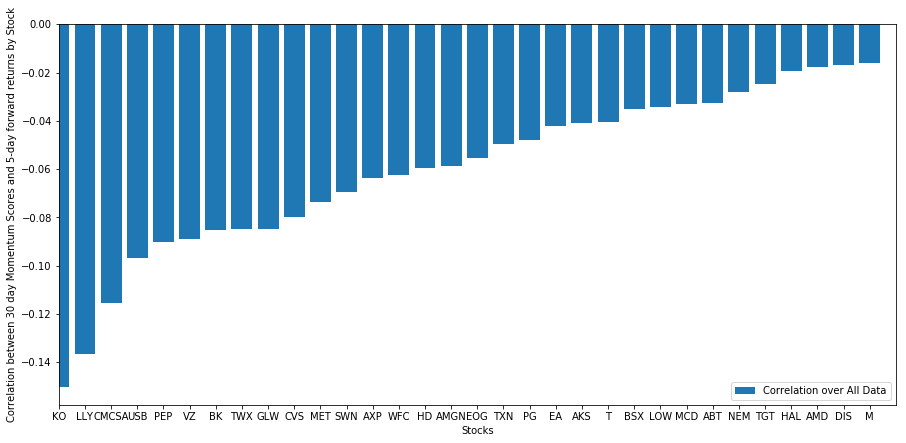
Semua saham kita mempunyai pembalikan purata ke tahap tertentu! (Jelas, alam semesta yang kita pilih berfungsi seperti ini.) Ini memberitahu kita bahawa jika saham menduduki tempat teratas dalam analisis momentum, kita harus mengharapkan mereka untuk melakukan dengan buruk minggu depan.

Hubungan antara kedudukan skor analisis momentum dan pulangan

Seterusnya, kita perlu melihat korelasi antara skor kedudukan kita dan pulangan hadapan keseluruhan pasaran, iaitu hubungan antara kadar pulangan yang diramalkan dan faktor kedudukan kita.

Untuk tujuan ini, kami mengira korelasi harian antara momentum 30 hari semua saham dan pulangan jangka masa 1 minggu.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

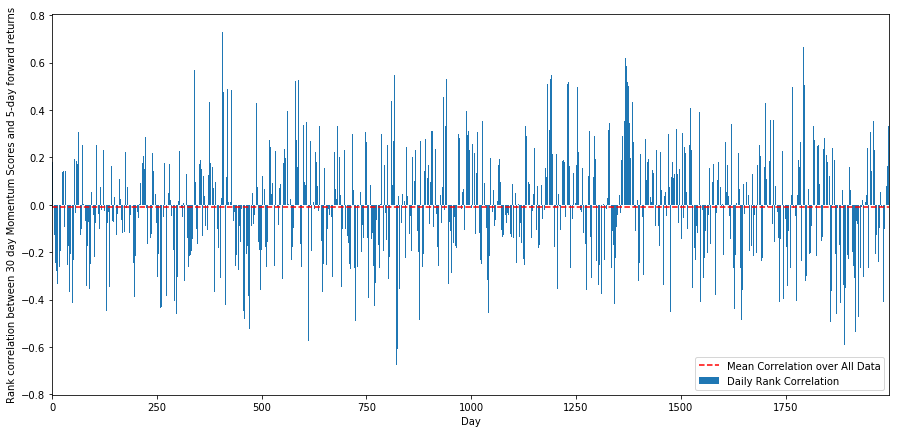
Korrelasi harian menunjukkan korelasi yang sangat kompleks tetapi sangat kecil (yang diharapkan kerana kita mengatakan semua stok akan kembali ke purata).

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

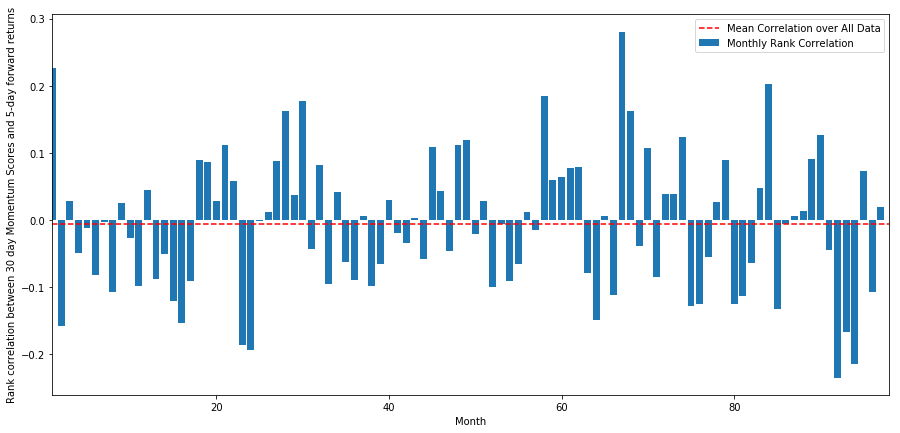
Kita boleh lihat bahawa korelasi purata adalah negatif sekali lagi, tetapi ia juga berubah setiap bulan.

Pendapatan purata pada bakul stok

Kami telah mengira pulangan pada bakul saham yang diambil daripada kedudukan kami. jika kami memberi kedudukan kepada semua stok dan membahagikannya kepada nn kumpulan, apakah purata pulangan setiap kumpulan?

Langkah pertama adalah untuk membuat fungsi yang akan memberikan pulangan purata dan faktor kedudukan setiap bakul yang diberikan setiap bulan.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Apabila kita menilai saham berdasarkan skor ini, kita mengira purata pulangan setiap bakul. Ini harus membolehkan kita memahami hubungan mereka untuk masa yang lama.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

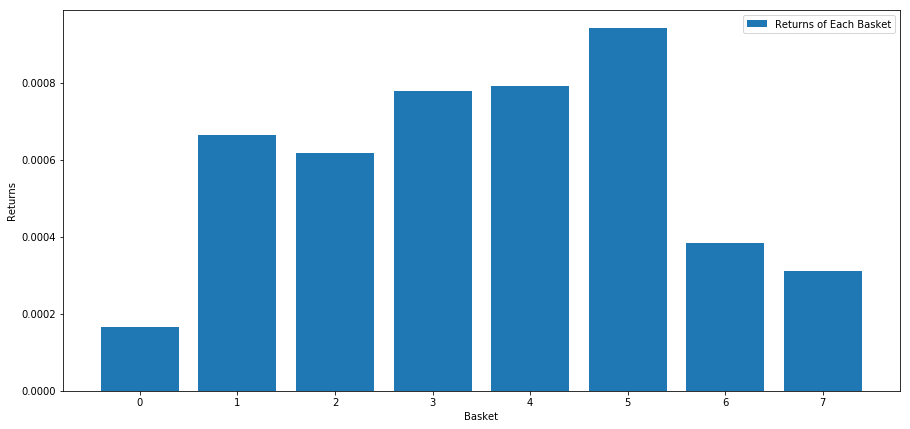
Nampaknya kita boleh memisahkan pelaku yang berprestasi tinggi dari pelaku yang kurang.

Kesesuaian margin (dasar)

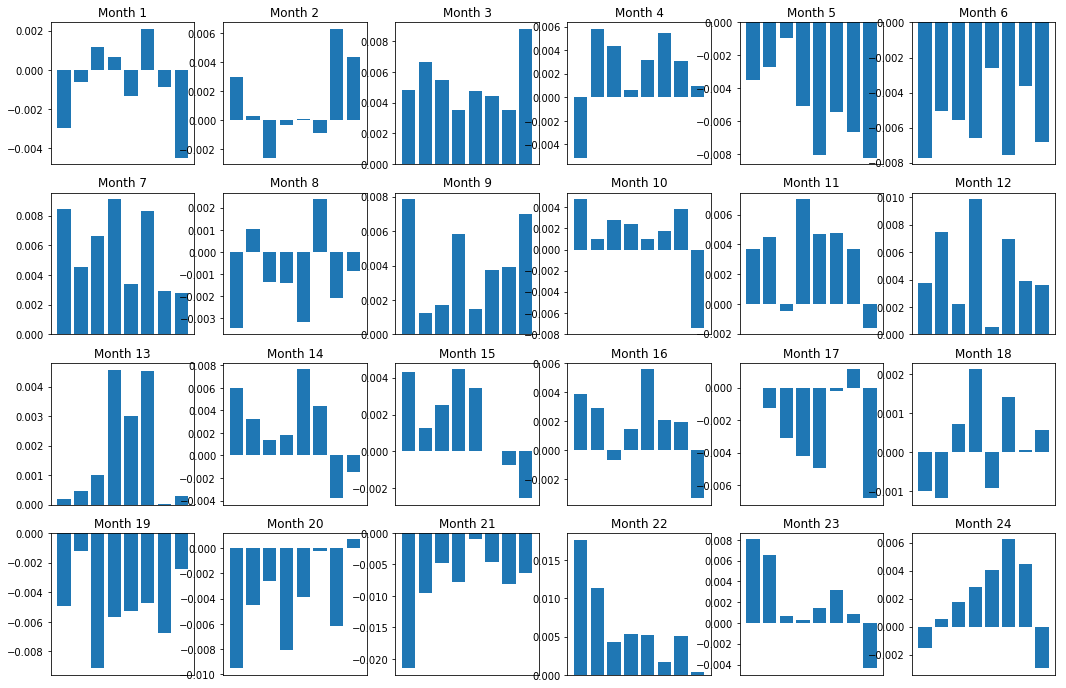
Sudah tentu, ini hanya hubungan purata. Untuk memahami betapa konsistennya hubungan dan sama ada kita bersedia untuk berdagang, kita harus mengubah pendekatan dan sikap kita terhadapnya dari masa ke masa. Seterusnya, kita akan melihat margin faedah bulanan mereka (basis) untuk dua tahun sebelumnya. Kita boleh melihat lebih banyak perubahan dan menjalankan analisis lanjut untuk menentukan sama ada skor momentum ini boleh diperdagangkan.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

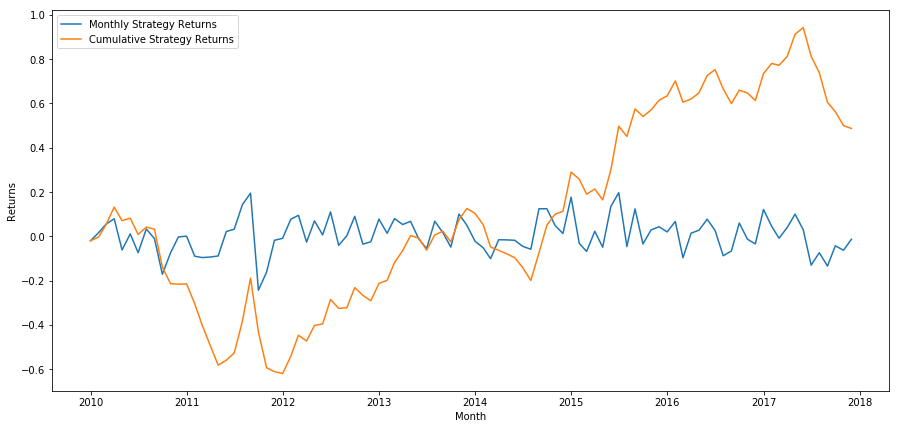
Akhirnya, jika kita pergi panjang bakul terakhir dan pergi pendek bakul pertama setiap bulan, maka mari kita lihat pulangan (mengandaikan peruntukan modal yang sama setiap sekuriti).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Kadar pulangan tahunan: 5.03%

Kita dapat melihat bahawa kita mempunyai skim kedudukan yang sangat lemah, yang hanya dapat membezakan saham prestasi tinggi dari saham prestasi rendah.

Cari skim kedudukan yang betul

Untuk merealisasikan strategi ekuiti seimbang jangka pendek, sebenarnya, anda hanya perlu menentukan skim kedudukan. Semua sesudah itu adalah mekanikal. Setelah anda mempunyai strategi ekuiti seimbang jangka pendek, anda boleh menukar faktor kedudukan yang berbeza tanpa banyak perubahan. Ini adalah cara yang sangat mudah untuk mengulangi idea anda dengan cepat tanpa perlu bimbang tentang menyesuaikan semua kod setiap kali.

Skema kedudukan juga boleh datang dari hampir mana-mana model. Ia tidak semestinya model faktor berasaskan nilai. Ia boleh menjadi teknologi pembelajaran mesin yang dapat meramalkan pulangan sebulan lebih awal dan memberi kedudukan mengikut tahap ini.

Pemilihan dan penilaian skim kedudukan

Skim kedudukan adalah kelebihan dan bahagian yang paling penting dalam strategi ekuiti yang seimbang jangka pendek.

Titik permulaan yang baik adalah untuk memilih teknologi yang sedia ada dan melihat jika anda boleh mengubahsuai mereka sedikit untuk mendapatkan pulangan yang lebih tinggi.

• Klon dan penyesuaian: Pilih topik yang sering dibincangkan, dan lihat apakah anda dapat mengubahnya sedikit untuk mendapatkan kelebihan. Secara umum, faktor yang tersedia untuk umum tidak lagi mempunyai isyarat perdagangan, kerana mereka telah sepenuhnya melakukan arbitrage dari pasaran. Tetapi kadang-kadang mereka akan membawa anda ke arah yang betul.

• Model harga: Mana-mana model yang meramalkan pulangan masa depan boleh menjadi faktor yang berpotensi digunakan untuk memberi kedudukan kepada bakul objek perdagangan anda.

• Faktor berasaskan harga (penunjuk teknikal): faktor berasaskan harga, seperti yang dibincangkan hari ini, mendapatkan maklumat mengenai harga sejarah setiap ekuiti dan menggunakannya untuk menjana nilai faktor.

• Regresi dan momentum: Perlu diperhatikan bahawa beberapa faktor percaya bahawa apabila harga bergerak ke satu arah, mereka akan terus melakukannya, sementara beberapa faktor adalah sebaliknya. Kedua-duanya adalah model yang berkesan untuk jangka masa dan aset yang berbeza, dan penting untuk mengkaji sama ada tingkah laku asas berdasarkan momentum atau regresi.

• Faktor asas (berasaskan nilai): Ini adalah gabungan nilai asas, seperti PE, dividen, dll. Nilai asas mengandungi maklumat yang berkaitan dengan fakta dunia sebenar syarikat, jadi ia boleh lebih kuat daripada harga dalam banyak aspek.

Pada akhirnya, ramalan pembangunan adalah perlumbaan persenjataan, dan anda cuba untuk kekal satu langkah ke depan. faktor akan menjadi arbitrage dari pasaran dan mempunyai hayat yang berguna, jadi anda mesti sentiasa bekerja untuk menentukan berapa banyak kemelesetan faktor anda telah mengalami dan apa faktor baru boleh digunakan untuk menggantikannya.

Pertimbangan lain

• Kekerapan imbangan semula

Setiap sistem kedudukan meramalkan pulangan dalam jangka masa yang sedikit berbeza. Regresi purata berdasarkan harga mungkin dapat diramalkan dalam beberapa hari, sementara model faktor berdasarkan nilai mungkin meramalkan dalam beberapa bulan. Adalah penting untuk menentukan julat masa yang harus diramalkan oleh model, dan melakukan pengesahan statistik sebelum melaksanakan strategi. Sudah tentu, anda tidak mahu terlalu sesuai dengan cuba mengoptimumkan kekerapan imbangan semula. Anda pasti akan menemui kekerapan rawak yang lebih baik daripada kekerapan lain. Setelah anda menentukan julat masa ramalan skema kedudukan, cuba imbangan semula pada kira-kira kekerapan ini untuk memanfaatkan sepenuhnya model anda.

• Kapasiti modal dan kos urus niaga

Setiap strategi mempunyai jumlah modal minimum dan maksimum, dan ambang minimum biasanya ditentukan oleh kos transaksi.

Perdagangan terlalu banyak saham akan membawa kepada kos transaksi yang tinggi. Jika anda ingin membeli 1,000 saham, ia akan menelan ribuan dolar pada setiap rebalancing. Asas modal anda mesti cukup tinggi supaya kos transaksi dapat menyumbang sebahagian kecil daripada pulangan yang dihasilkan oleh strategi anda. Sebagai contoh, jika modal anda adalah $ 100,000 dan strategi anda memperoleh 1% ($ 1,000) sebulan, semua pulangan ini akan dikonsumsi oleh kos transaksi. Anda perlu menjalankan strategi dengan berjuta-juta dolar modal untuk memperoleh lebih daripada 1,000 saham.

Sempadan aset terendah terutamanya bergantung kepada bilangan saham yang didagangkan. Walau bagaimanapun, kapasiti maksimum juga sangat tinggi. Strategi ekuiti seimbang jangka pendek boleh berdagang beratus juta dolar tanpa kehilangan kelebihan. Ini adalah fakta, kerana strategi ini agak jarang untuk rebalancing. Nilai dolar setiap saham akan sangat rendah apabila jumlah aset dibahagikan dengan jumlah saham yang didagangkan. Anda tidak perlu bimbang sama ada jumlah dagangan anda akan mempengaruhi pasaran. Katakan anda berdagang 1,000 saham, iaitu 100,000,000 dolar. Jika anda menyeimbangkan semula keseluruhan portfolio setiap bulan, setiap saham hanya akan berdagang $ 100,000 sebulan, yang tidak mencukupi untuk menjadi pasaran penting untuk kebanyakan sekuriti.