Medir o Risco e o Retorno - Uma Introdução à Teoria Markowitz

Na semana passada, ao introduzirComo medir o risco de posição - Introdução ao método VaREm um artigo publicado na Revista de Investimentos, o autor da pesquisa sobre o risco de um portfólio de ativos disse que o risco de um portfólio não é igual aos riscos de ativos individuais e está relacionado à sua correlação de preço. Tomando dois ativos como exemplo, se sua correlação positiva for muito forte, ou seja, eles aumentam e caem juntos, então os investimentos diversificados não reduzirão o risco. Se houver uma forte correlação negativa, os investimentos diversificados podem reduzir o risco significativamente.

A Teoria Moderna de Portfólio (MPT), proposta por Harry Markowitz em 1952, é uma estrutura matemática para a seleção de portfólios. Ela visa maximizar os retornos esperados escolhendo diferentes combinações de ativos de risco enquanto controla o risco. A ideia central é que os preços dos ativos não se movem completamente em sincronia uns com os outros (ou seja, há uma correlação incompleta entre os ativos), e o risco geral de investimento pode ser reduzido através da alocação diversificada de ativos.

O conceito-chave da Teoria de Markowitz

1. Taxa de retorno esperada: Este é o rendimento que os investidores esperam receber da detenção de ativos ou de uma carteira de investimento, geralmente previsto com base em dados históricos de rendimento.

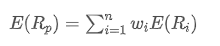
Onde?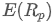é o rendimento esperado da carteira,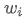é o peso do i-ésimo activo da carteira,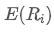é o rendimento esperado do i-o activo.

2. Risco (volatilidade ou desvio-padrão): Utilizado para medir a incerteza dos retornos dos investimentos ou a volatilidade dos investimentos.

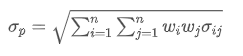
Onde?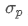Representa o risco total da carteira,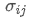é a covariância do activo i e do activo j, que mede a relação de variação de preços entre estes dois activos.

3. Covariância: mede a relação mútua entre as variações de preço de dois activos.

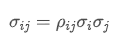
Onde?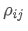é o coeficiente de correlação do activo i e do activo j,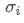e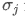são, respectivamente, os desvios-padrão do activo i e do activo j.

4. Fronteira eficiente: No sistema de coordenadas risco-rendimento, a fronteira eficiente é o conjunto de carteiras de investimento que podem proporcionar o rendimento máximo esperado num determinado nível de risco.

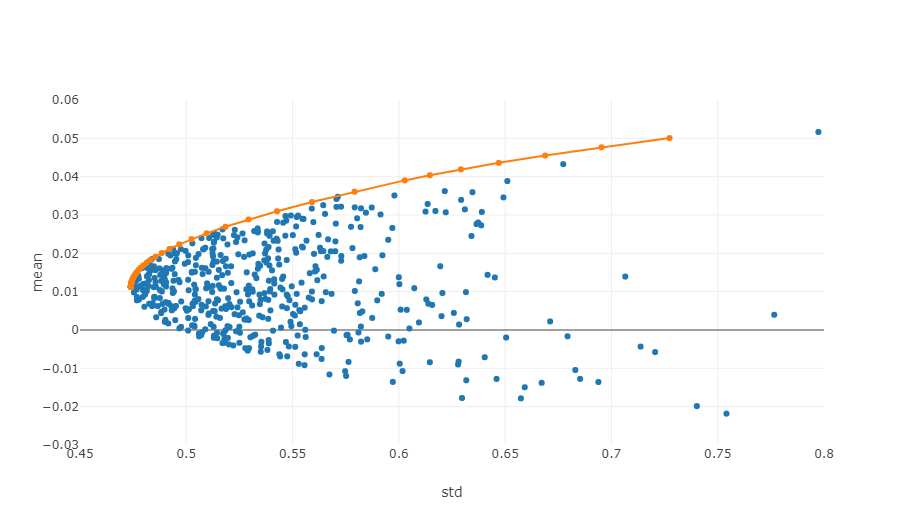
O diagrama acima é uma ilustração de uma fronteira eficiente, onde cada ponto representa uma carteira de investimento ponderada diferente. O eixo x denota volatilidade, que equivale ao nível de risco, enquanto o eixo y significa taxa de retorno.

Em negociação quantitativa e gerenciamento de carteiras, a aplicação desses princípios requer análise estatística de dados históricos e o uso de modelos matemáticos para estimar retornos esperados, desvios padrão e covariâncias para vários ativos. Em seguida, técnicas de otimização são usadas para encontrar a melhor alocação de peso de ativos. Este processo geralmente envolve operações matemáticas complexas e extenso processamento de computador - é por isso que a análise quantitativa se tornou tão importante nas finanças modernas. Em seguida, ilustraremos como otimizar com exemplos específicos do Python.

Exemplo de código Python para encontrar a combinação ideal usando o método de simulação

O cálculo do portfólio óptimo de Markowitz é um processo de várias etapas, que envolve várias etapas-chave, como a preparação de dados, simulação de portfólio e cálculo de indicadores.https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Obter dados de mercado:

Através doget_dataOs dados utilizados para calcular os retornos e os riscos são os dados necessários para a construção de carteiras de investimento e para o cálculo dos rácios Sharpe.

2. Calcular a taxa de retorno e o risco:

Ocalculate_returns_riskA função foi usada para calcular os retornos anualizados e o risco anualizado (desvio padrão) para cada moeda digital.

3. Calcule a carteira óptima de Markowitz:

Ocalculate_optimal_portfolioEm cada simulação, foram geradas ponderações aleatórias dos ativos e, em seguida, o rendimento e o risco esperados da carteira foram calculados com base nesses ponderações. Ao gerar combinações aleatórias com diferentes pesos, é possível explorar várias carteiras de investimento potenciais para encontrar a ideal.

O objetivo de todo o processo é encontrar o portfólio de investimento que produz os melhores retornos esperados em um determinado nível de risco. Simulando múltiplas combinações possíveis, os investidores podem entender melhor o desempenho de diferentes configurações e escolher a combinação que melhor se adapte aos seus objetivos de investimento e tolerância ao risco.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

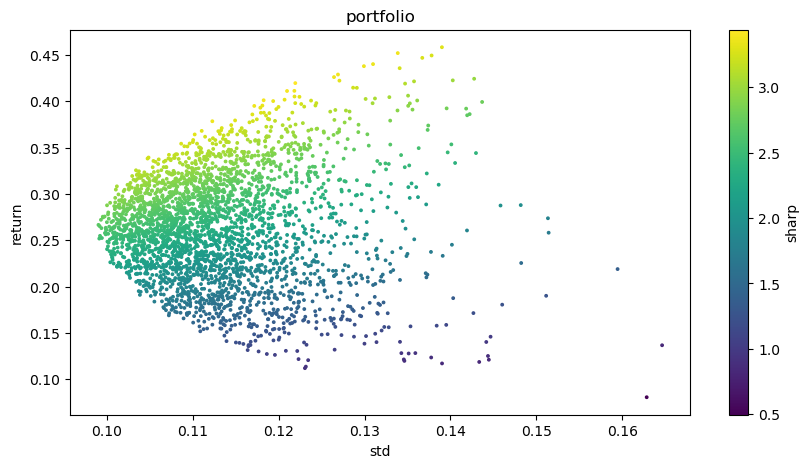
# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Resultado final de saída: Combinação ideal: Peso do BTCUSDT: 0,0721 Peso do ETHUSDT: 0,2704 Peso do BNBUSDT: 0,3646 Peso do LINKUSDT: 0,1892 Peso do BCHUSDT: 0,0829 Peso do LTCUSDT: 0,0209 Taxa de retorno esperada: 0,4195 Risco esperado (desvio-padrão): 0,1219 Relação Sharpe: 3.4403