Estratégia de negociação de alta frequência de livro de ordens baseada em aprendizado de máquina

• ### A teoria.

O mecanismo de negociação do mercado de valores pode ser dividido em dois tipos de mercado de oferta e mercado de ordens, o primeiro dependendo de ser um comerciante de mercado para fornecer liquidez, o segundo é fornecido por meio de uma lista de preços de limite, a negociação é formada por compras e vendas de investidores através de um leilão de compra e venda. O mercado de valores da China pertence ao mercado de ordens, incluindo o mercado de ações e o mercado de futuros.

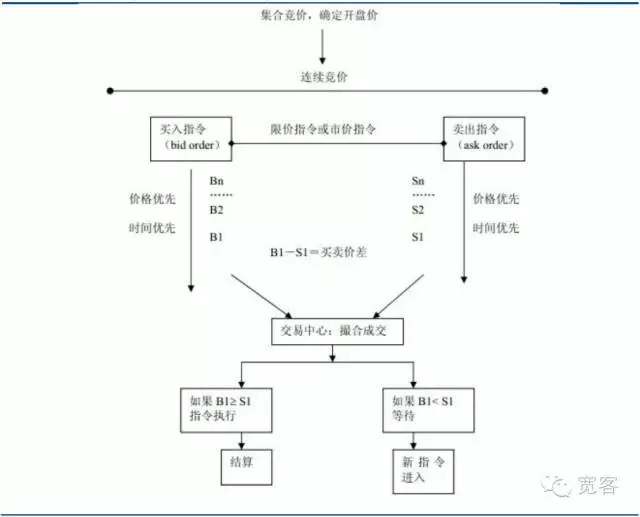Gráfico 1 Diagrama do mercado de ordens

• (I) Um livro de pedidos de preço limitado

  O estudo do livro de pedidos pertence à categoria de estudos de microestrutura de mercado. A teoria da microestrutura de mercado baseia-se na teoria dos preços e na teoria dos fabricantes da microeconomia como fonte de suas ideias, enquanto que na análise de seus principais problemas, como o processo e as causas da formação de preços de transações de ativos financeiros, o equilíbrio geral, o equilíbrio local, o lucro marginal, o custo marginal, a continuidade do mercado, a teoria dos estoques, a teoria dos jogos e a economia da informação.

  De acordo com o progresso da pesquisa no exterior, a área de microestrutura de mercado é representada por O’Hara, e a maioria das teorias é baseada em mercados de mercado (ou seja, mercados movidos por ofertas), como modelos de estoque e modelos de informação. No ano passado, o mercado de negociação real foi gradualmente dominado por pedidos, mas menos pesquisas foram feitas especificamente para mercados movidos por pedidos.

  O mercado de valores e o mercado de futuros domésticos pertencem ao mercado movido por ordens. A imagem abaixo é uma cópia do Livro de Pedidos do Livro de Pedidos do Livro de Pedidos do IF1312. Não há muita informação obtida diretamente de cima. A informação básica inclui um preço de compra, um preço de venda, um volume de compra e um volume de venda.

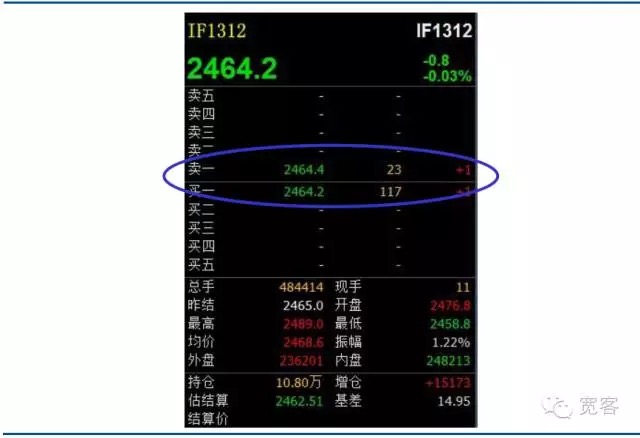  Gráfico 2 Livro de pedidos de índices acionários de contratos de força principal de futuros de nível 1

• (ii) Progresso no estudo de transações de alta frequência em carteiras de pedidos

  A modelagem dinâmica dos livros de pedidos, há dois métodos principais, um é o método clássico de economia de medida, o outro é o método de aprendizagem de máquina. O método de economia de medida é um método de pesquisa clássico e dominante, como a desagregação de MRR para análise de diferença de preço, a desagregação de Huang e Stoll, etc., o modelo de ACD para a duração do pedido, o modelo logístico para a previsão de preços.

  A aprendizagem de máquina também é muito ativa em pesquisas acadêmicas na área financeira, como o estudo de 2012 sobre as tendências de previsão de alta frequência do índice KOSPI200 usando classificadores de aprendizagem. É um pensamento de pesquisa comum, que utiliza os indicadores comuns da análise técnica (MA, EMA, RSI, etc.) para fazer previsões de mercado.

• Aplicação da aprendizagem de máquina em transações de alta frequência em carteiras de pedidos

  • #### (I) Mapa da arquitetura do sistema

  O gráfico abaixo é uma estrutura de sistema de uma típica estratégia de negociação de aprendizagem de máquina, que inclui dados de livro de pedidos, descoberta de características, construção e validação de modelos e vários módulos principais de oportunidades de negociação. É importante notar que o processo de negociação é acionado por eventos de mercado, sendo a chegada de tick um desses eventos.

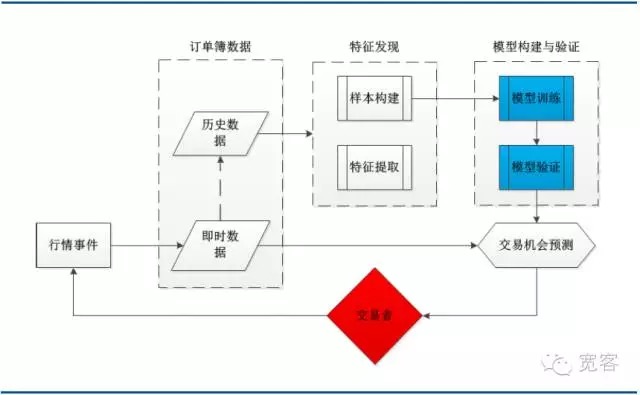  Gráfico 3 - Arquitetura de sistemas para modelagem de livros de pedidos baseada em aprendizado de máquina

  • #### (b) Apresentação do vector de suporte

  Na década de 1970, Vapnik e outros começaram a construir um sistema teórico mais completo de SLT (Teoria de Aprendizagem Estatística), que foi usado para estudar as propriedades estatísticas e métodos de aprendizagem em situações de amostra limitada, criando uma boa estrutura teórica para problemas de aprendizagem de máquina de amostra limitada, melhor resolvendo problemas práticos como amostra pequena, não-linear, alta dimensão e ponto mínimo local. Em 1995, Vapnik e outros explicitamente propuseram um novo método de aprendizagem universal para suportar vectores de máquina SVM (Support Vector Machine), a teoria recebeu ampla atenção e foi aplicada a diferentes áreas, e inicialmente apresentou muitas vantagens em relação aos seus próprios métodos.

  O SVM evoluiu a partir do superplano de classificação ótima em situações linearmente divisíveis. Para as questões de classificação de duas classes, o conjunto de amostras de treinamento é definido como: ((xi,yi), i = 1,2 … l, l é o número de amostras de treinamento, xi é a amostra de treinamento, yi pertence a {-1 + 1} é o marcador de classe de entrada da amostra xi ((output esperado)). O ponto de partida do algoritmo SVM é encontrar o superplano de classificação ótimo.

  O superplano de classificação ótima não só separa todas as amostras corretamente, mas também permite que o limite entre as duas categorias seja o máximo, definido como a soma da menor distância entre o conjunto de dados de treinamento e o superplano de classificação. O superplano de classificação ótima significa o menor erro de classificação médio para os dados de teste.

  Se houver um superplano em um espaço vetorial d-dimensional:

  F(x)=w*x+b=0

  Separando os dois tipos de dados acima, o superplano é chamado de interface.*x é o produto interno de dois vetores w e x em um espaço vetorial de dimensões d.

  Se a interface for:

  w*x+b=0

  A interface que permite que a distância entre as duas classes de amostras mais próximas da interface seja maior (margem) é chamada de interface ótima.

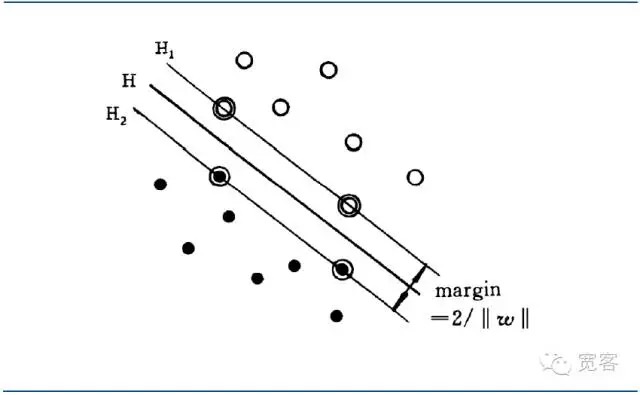  Gráfico 4 Diagrama da interface de classificação do SVM

  A unificação da equação da interface ótima permite que a distância entre as duas classes de amostras

  

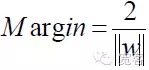
  Então, para qualquer amostra, temos

  

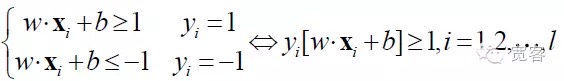
  Para obter uma interface ótima, além de satisfazer a fórmula acima, você também deve minimizar.

  Assim, o modelo matemático do problema SVM é:

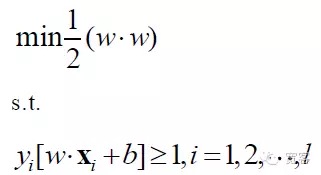
  O SVM acabou se tornando um problema de planejamento otimizado, com o foco de pesquisa acadêmica focado em soluções rápidas e sua disseminação para aplicações multidisciplinares e práticas.

  O SVM foi originalmente proposto para problemas de classificação binária e, de acordo com os requisitos atuais de aplicação, foi expandido para problemas de multiclassificação. Algoritmos de multiclassificação já existentes incluem um par de múltiplos, um para um, codificação de erro, DAG-SVM e classificadores de SVM de classe i, entre outros.

  • #### (III) Extração de índices de livros de pedidos

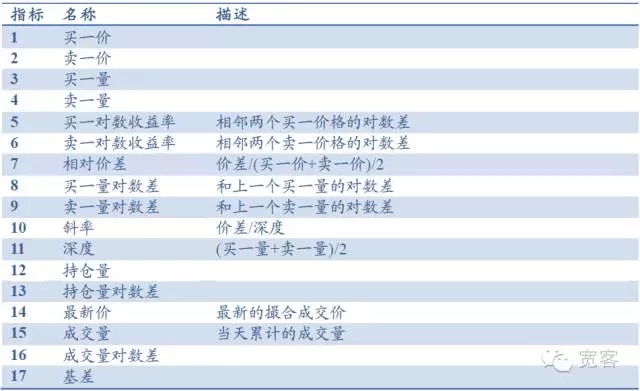
  Por exemplo, a carteira de pedidos inclui principalmente indicadores básicos, como preço de compra, preço de venda, quantidade de compra e quantidade de venda, e pode derivar indicadores como profundidade, inclinação e diferença de preço relativo. Outros indicadores incluem volume de posse, volume de transação e diferença de base, totalizando 17 indicadores, como mostrado na tabela a seguir. Também pode ser introduzido indicadores de análise técnica comuns, como RSI, KDJMA, EMA, etc.

  Tabela 1 Repositório de indicadores baseado no livro de pedidos do Level

  

  • #### (iv) Desenhos de características dinâmicas e oportunidades de negociação dos livros de pedidos

  Do ponto de vista do microscópio de mercado, existem dois métodos para medir a dinâmica dos preços em curto prazo, um é a dinâmica do preço médio, e o outro é a dinâmica do preço intermédio. Este artigo escolheu a dinâmica do preço médio mais simples e intuitiva.

  

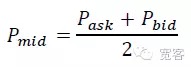
  De acordo com o livro de pedidos, o tamanho da variação de ΔP no preço médio dentro de Δt é dividido em três categorias:

  O gráfico abaixo mostra a distribuição da dinâmica do preço médio do contrato principal IF1311 em 29 de outubro, com 32400 ticks por dia.

  No caso de Δt = 1 tick, o valor absoluto de variação do preço médio é de 0,2 cerca de 6000 vezes, o valor absoluto de variação é de 0,4 cerca de 1500 vezes, o valor absoluto de variação é de 0,6 cerca de 150 vezes, o valor absoluto de variação é de 0,8 maior que 50 vezes, o valor absoluto de variação é maior que igual a 1 cerca de 10 vezes.

  No caso de Δt = 2tick, o valor médio varia em absoluto de 0,2 cerca de 7000 vezes, o valor absoluto de 0,4 cerca de 3000 vezes, o valor absoluto de 0,6 cerca de 550 vezes, o valor absoluto de 0,8 cerca de 205 vezes, o valor absoluto de variação maior que igual a 1 cerca de 10 vezes.

  Consideramos as oportunidades potenciais de negociação quando o valor absoluto de variação é maior que 0,4. No caso Δt = 1 tick, há cerca de 1700 oportunidades por dia; no caso Δt = 2 tick, há cerca de 4000 oportunidades por dia.

  

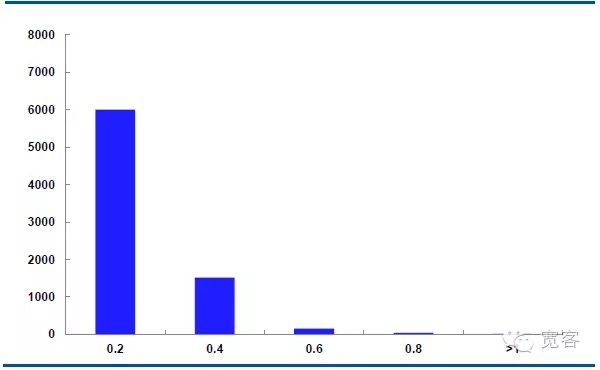
  Figura 5 Distribuição da variação do preço médio em 29 de outubro (Δt = 1 tick)

  

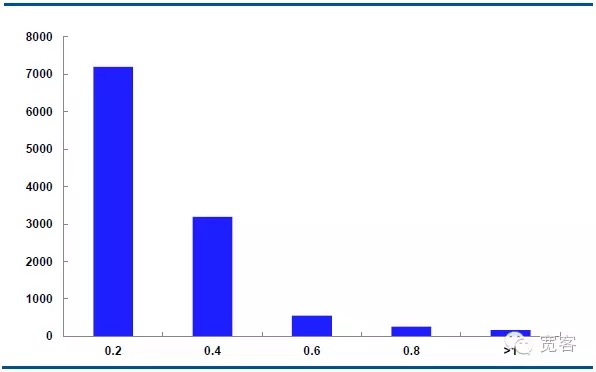
  Figura 6 Distribuição da variação do preço médio em 29 de outubro (Δt = 2 tick)

• Três, estratégias e evidências.

Como o modelo SVM tem uma alta complexidade de treinamento em grandes amostras e um tempo de treinamento mais longo, nós escolhemos um período de tempo relativamente curto de dados históricos, usando o exemplo do contrato IF1311 com o nível_1 em outubro para validar a eficácia do modelo.

• (I) Teste de eficácia do modelo

  Ciclo de dados: Contrato IF1311 em outubro;

  Δt valorização: Quanto menor o Δt, maior o requisito de detalhes de transação, quando Δt = 1 tick, é difícil obter lucro na transação real, para comparar o efeito do modelo, aqui valorizamos 1 tick, 2 tick e 3 tick, respectivamente;

  Indicadores de avaliação do modelo: precisão da amostra, precisão do teste, tempo de previsão. 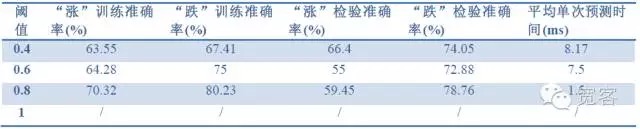Tabela 2 Previsão de 1 tick com dados de 1 tick

  Tabela 3 Previsão de tick 2 com dados de tick 1

  Tabela 4 Previsão de 2tick com dados de 2tick

  A partir dos dados das três tabelas acima, podemos tirar algumas conclusões: A maior precisão é de cerca de 70%, e a mais de 60% pode ser convertida em uma estratégia de negociação.

• (ii) estratégia de simulação de receita

  Por exemplo, no dia 31 de outubro, nós fizemos uma simulação de negociação, a taxa de comissão de negociação de futuros de índices de ações da instituição é geralmente a taxa de comissão de negociação de futuros de índices de ações da instituição é geralmente de 0,²⁶⁄₁₀₀₀₀, e nós assumimos que o número de transações não tem limite de recebimento, e assumimos que o preço de desvio unilateral de 0,2 pontos por transação e o número de transações de baixa é de 1 mão.

  Tabela 5 Simulação de estratégias de negociação em 31 de outubro

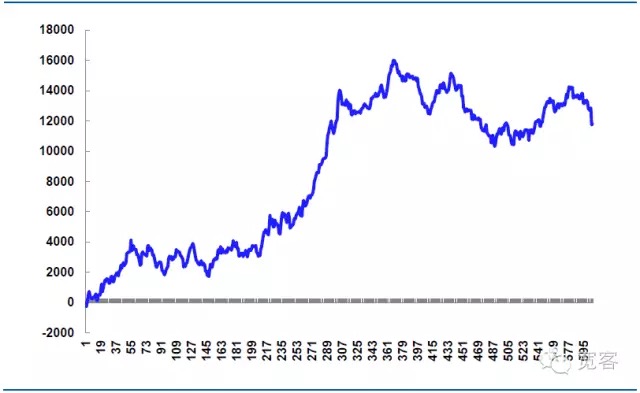
  O número de transações no dia foi de 605, incluindo transações em trâmite, 339 lucros, 56% de vitórias, com lucro líquido de 11814,99 yuan.

  O preço de desvio teórico é de 14.520 yuan, que é parte da chave para a batalha real da estratégia. Se os detalhes do pedido forem controlados com mais precisão, o preço de desvio pode ser reduzido e o lucro líquido aumentado. Se os detalhes do pedido não forem controlados adequadamente ou se a volatilidade do mercado for anormal, o preço de desvio será maior e o lucro líquido será reduzido, portanto, o sucesso ou o fracasso da negociação de alta frequência geralmente depende da execução dos detalhes.

  Gráfico 7 Resultados da simulação em 31 de outubro

O artigo foi originalmente publicado em The New York Times, e foi traduzido para o português por: