Declaração de direitos autorais: Se você quiser copiar o código deste artigo, por favor, indique a fonte, se for para uso comercial, escreva o artigo por favor, escreva pessoalmente ou entre em contato com o autor pelo e-mail [email protected]

1. Introdução

Os benefícios da quantidade

A negociação quantitativa refere-se a um julgamento subjetivo feito por humanos em vez de modelos matemáticos avançados, que utilizam a tecnologia de computador para criar estratégias que utilizam uma grande quantidade de dados históricos para criar uma grande variedade de eventos de probabilidade e probabilidade de ganhos excessivos, reduzindo drasticamente o impacto das flutuações de emoção dos investidores e evitando decisões de investimento irracionais em situações de mercado extremamente frenético ou pessimista. A moeda digital é uma das principais fontes de receita para o mundo.*A continuidade do mercado de negociação sem interrupção de 7 horas e a negociação quantitativa pode atingir o efeito de negociação de alta frequência, é obviamente um bom começo para a quantificação a partir do mercado de moeda digital. O mercado de moeda digital ainda não está maduro.

GQNR Modelo 2

Este modelo é baseado no modelo de Garch para a previsão da taxa de flutuação, utilizando regressão não linear, por exemplo, a GA para a previsão do VaR superior e inferior no próximo ciclo futuro, usando a regressão decimal para o valor de VaR que prevê a taxa de flutuação. Este método é conhecido como GQNR.

1. Módulo Garch

Esta seção irá detalhar a dedução do núcleo da estratégia Garch, que tem uma certa universalidade nos mercados financeiros e pode alcançar um certo efeito de previsão em moedas digitais.

1.1 Definição de Garch

A essência do modelo ARCH é o uso de uma sequência de quadrados de residuos para a aplicação de um plano móvel de grau q para o valor da função de diferença de curto prazo. Como o modelo de média móvel possui um intervalo de grau q para o coeficiente de correlação automática, o modelo ARCH só se aplica a um coeficiente de correlação automática de curto prazo da função de diferença de diferença. No entanto, na prática, algumas funções de diferença diferencial de sequências de residuos são auto-referenciais a longo prazo. Usar a função de diferença diferencial de adequação do modelo ARCH produzirá uma média móvel muito alta, aumentando a dificuldade de estimar os parâmetros e, finalmente, afetando a precisão de adequação do modelo ARCH.           Para corrigir um problema, foi proposto um modelo de diferença condicional de regressão de sentido amplo, abreviado como GARCH ((p,q). O modelo GARCH na verdade é baseado no ARCH, que é formado pela regressão da função diferencial p-classe, que pode ser efetivamente aplicada a funções diferencials com memória de longo prazo. O modelo ARCH é um exemplo especial do modelo GARCH, o modelo GARCH p=0 (p,q).

1.2 Processo ARCH

       define σn como a taxa de flutuação estimada do ativo no n-ésimo ciclo de negociação, mu é a taxa de retorno diária, então pode ser feita uma estimativa não tendenciosa com base na taxa de retorno dos últimos m ciclos de negociação: $\( \sigma *n^2= \frac{1}{m-1} \sum\limits*{i=1}^m {( { \mu_{n-i}- \overline{\mu} } ) ^2}, \)\(         Faça as seguintes mudanças: 1 permita que μn-i seja a taxa de retorno percentual; 2 permita que m-1 seja a taxa de retorno percentual; 3 assume que μ = 0 e que essas mudanças não afetam muito o resultado. De acordo com a fórmula acima, a taxa de flutuação pode ser simplificada para: \)\( \sigma *n^2= \frac{1}{m} \sum\limits*{i=1}^m { \mu_{n-i} ^2}, \)\(         ou seja, o quadrado da taxa de flutuação de cada período tem o mesmo peso 1/m, uma vez que é a estimativa da taxa de flutuação atual, os dados mais próximos devem ser atribuídos maior peso, então a fórmula pode ser alterada para: \)\( \sigma *n^2= \sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)$         αi é o coeficiente do quadrado da taxa de retorno do ciclo de negociação i, sendo positivo e quanto menor o valor de i, maior a soma dos pesos. Para uma generalização mais ampla, assumindo que existe uma diferença de taxa de diferença de longo prazo VL, e o correspondente peso é γ, pode ser obtido de acordo com a fórmula acima:

\[ \begin{cases}\sigma *n^2= \gamma V*{L}+\sum\limits_{i=1}^m { \alpha_i\mu_{n-i} ^2}\ &\ \gamma+\sum\limits_{i=1}^m{\alpha_i\mu_{n-i}^2}=1 & \end{cases} , \]

        O queω = γVL, fórmula(15) pode ser reescrito como: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}, \)\(         De acordo com a fórmula acima, podemos obter o processo comum ARCH \)\( \sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2}, \)$

1.3 Processo GARCH

O modelo GARCH (p,q) é uma combinação dos modelos ARCH (p) e EWMA (q), o que significa que a taxa de flutuação não está relacionada apenas com os ganhos do período p anterior, mas também com o próprio período q anterior, expressa da seguinte forma: $\( \sigma *n^2= \omega+\sum\limits*{i=1}^m { \alpha_i\mu_{n-i} ^2}+\sum\limits_{i=1}^m { \beta_i\sigma_{n-i} ^2}, \)\(         De acordo com a fórmula acima, podemos obter o comum GARCH ((1,1)): \)\( \begin{cases}\sigma *n^2= \omega+{ \alpha\mu*{n-1} ^2+\beta\sigma_{n-1}^2}\&\ \qquad\alpha+\beta+\gamma=1 & \end{cases} , \)$

2 módulos QR

        Este bloco irá explicar a regressão básica dos dígitos, descrevendo a importância dos dígitos estratégicos

2.1 Definição do QR

        A regressão decimal é um método de modelagem para estimar a relação linear entre um conjunto de variáveis de regressão X e os dígitos da variável Y a ser interpretada. O modelo de regressão anterior era, na verdade, uma expectativa condicional da variável explicada. Também se preocupava com a relação entre a variável explicada e a média da distribuição da variável explicada, o que era a fração. Foi proposto pela primeira vez por Koenker e Bassett em 1978.

2.2 De OLS para QR

O método de regressão geral é o quadrado de minimizar a soma de: $\( min \sum{({y_i- \widehat{y}*i })}^2 \)\( O objetivo da fração é minimizar o valor absoluto de erro ponderado com base na fórmula acima e: \)\( \mathop{\arg\min*\beta}\ \ \sum{[{\tau(y_i-X_i\beta)^++(1-\tau)(X_i\beta-y_i) ^+ }]} \)$

2.2 Visualização QR

Como você pode ver, todas as amostras são divididas em espaços diferentes por uma linha de regressão, que também é uma linha de divisão.

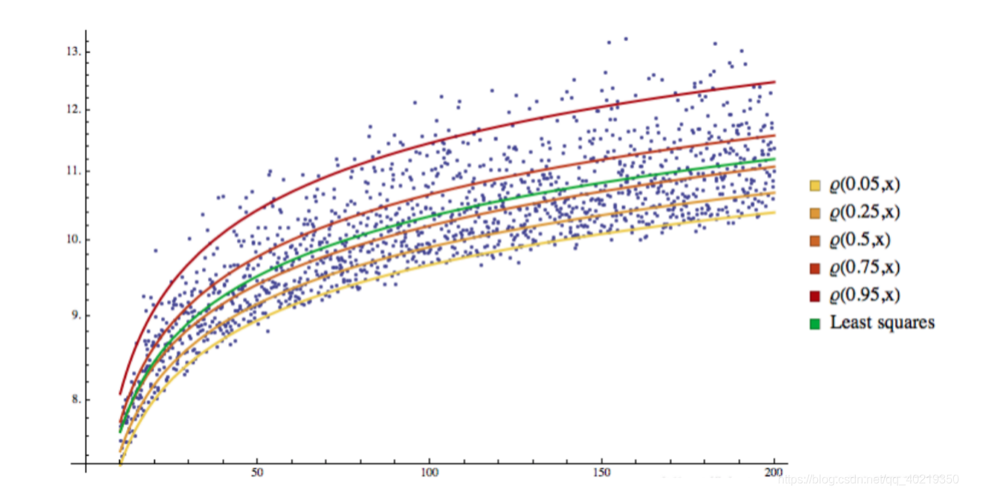
3. Regressão GARCH-QR

        Nós pensamos naturalmente, se você pode usar o mercado desconhecido taxa de flutuação sigma com o parâmetro Q, ou seja, VaR de regressão para prever o futuro probabilidade caso oscilação de queda, este setor vai seguir nesta direção.

3.1 Seleção da taxa de flutuação e forma de regressão do VaR

O blogueiro, que também é um dos fundadores do site, diz que a ideia é que o blogue seja uma forma de mostrar o que está acontecendo no país, e que o blogue seja uma forma de mostrar o que está acontecendo. $\( VaR=\epsilon+W^TE\E=(\zeta,\zeta^2,\zeta^3,\zeta^4)\W=(W_1,W_2,W_3,W_4) \)$

3.2 Determine a função alvo

        De acordo com as informações acima, podemos combinar e obter a função-alvo final para otimização: $\( \widehat{W}=\mathop{\arg\min_W}\ \ \sum{[{\alpha(VaR_t-W^TE_t)^++(1-\alpha)(W^TE_t-VaR_t) ^+ }]} \)$

3.3 Otimização de funções-alvo usando aprendizado de máquina

        Este passo é mais opcional, a escala tradicional é reduzida, também pode ser um algoritmo genético, o leitor pode usar sua própria criatividade para experimentar.Alguma coisa sobre o algoritmo GA

Como usar o GQNR na quantificação

1. Confirmação de ideias

O núcleo do GQNR está na volatilidade do mercado, em cada ponto do tempo atual, pode ser previsto através de GARCH para a previsão da volatilidade do próximo período, por outro lado, através de regresso numérico da volatilidade de previsão de dados passados, pode ser obtido um limiar de flutuação que não ultrapassa a maior probabilidade de fronteiras superiores e inferiores. Estas duas fronteiras são o núcleo do todo.

2. Dificuldades de utilização

• A forma de regressão
• Opções de algoritmos adaptativos
• Parâmetros apropriados para aprendizagem de máquina
• A incerteza e a aleatoriedade do mercado

3. Solução

• Reduzir o tempo de aprendizagem de estratégias
• Redução da garantia de depósito individual contra riscos de longo prazo
• Aumentar a co-validação de tendências de dupla linha de equilíbrio e a confirmação de subvalores secundários