Alho-poró e spread bid-ask: Um estudo preliminar sobre o modelo EKOP

• #### 1 Introdução

Recentemente, tenho sido muito ocupado, já se passaram alguns meses desde a última vez que escrevi um artigo. Muitas coisas aconteceram nestes meses, algumas das quais foram os piores dias da minha vida. Mas essas experiências me ensinaram que a vida, como o comércio, é cheia de altos e baixos e incertezas. Sempre esperamos aprender algo com o que já aconteceu, aproximando-nos lentamente da verdade que talvez não exista.

Todos sabemos que uma ação que está ativamente negociada geralmente tem uma diferença menor de compra e venda, enquanto uma ação que não está ativamente negociada tem o oposto. Por que isso acontece? Pode-se explicar a diferença de preços com um modelo matemático simples e bonito?[1] A proposta inicial foi para estudar se o comportamento de comerciantes com diferentes informações é a causa da diferença entre os dois tipos de preços de ações. Neste artigo de coluna, eu apresentarei a base deste modelo. A aplicação do modelo será analisada mais a fundo em artigos subsequentes (se eu tiver tempo para escrever). A beleza da simplicidade do modelo matemático é exposta neste artigo.

• #### 2 A hipótese do processo de transação

Quando falamos de um modelo financeiro, o mais importante é prestar atenção às hipóteses do modelo. Um bom modelo financeiro tem suas próprias hipóteses: não é tão forte que não seja universal; nem é tão fraco que não possa derivar resultados bonitos e concisos.

Hipótese 1: Estamos falando de uma transação de ações, com transações em dias separados e contínuas no dia. Isto é, as transações dos comerciantes ocorrem em 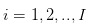entre esses dias de negociação separados. E, no dia de negociação, as transações ocorrem em 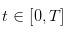em um tempo contínuo como esse.

• Em caso de má notícia, o valor das ações é
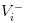
• A boa notícia é que nós registamos o valor das ações como
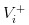
• Sem notícias, registamos o valor das ações como

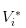
É óbvio que temos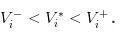

Hipótese 2: em um determinado dia, há α

A probabilidade de ocorrência de eventos que afetam o preço das ações é de 1-α para eventos que não afetam o preço das ações. Nos dias em que ocorrem eventos, há também a probabilidade de ocorrência de eventos negativos que reduzem o preço das ações, e a probabilidade de ocorrência de eventos positivos que aumentam o preço das ações.

Hipótese 3: Os participantes de negociação de ações são market makers (MM), informed traders (IT) e uninformed traders (UT). Eles seguem o seguinte comportamento de negociação:

MM está sempre pronto para colocar uma ordem de compra ou venda de uma unidade, fazendo sua obrigação como um comerciante de mercado. MM é neutro em relação ao risco, portanto, o preço que ele coloca é o preço justo que ele considera.

IT só negocia em dias de notícias, o seu comportamento é um processo de relaxamento. Um dia, se houver notícias ruins, ele vai colocar uma venda taxa de chegada de μ; e em dias de boas notícias, ele vai colocar uma taxa de chegada de μ.

A UT, ou seja, o nosso pobre espinafre, devido à vantagem da ausência de notícias, o seu comportamento de negociação também é um processo de relaxamento, e todos os dias, a taxa de chegada é a taxa de compra e venda. Observe que todos os processos de Poisson aqui são independentes uns dos outros. Podemos representar a hipótese 3 com um gráfico, como segue:

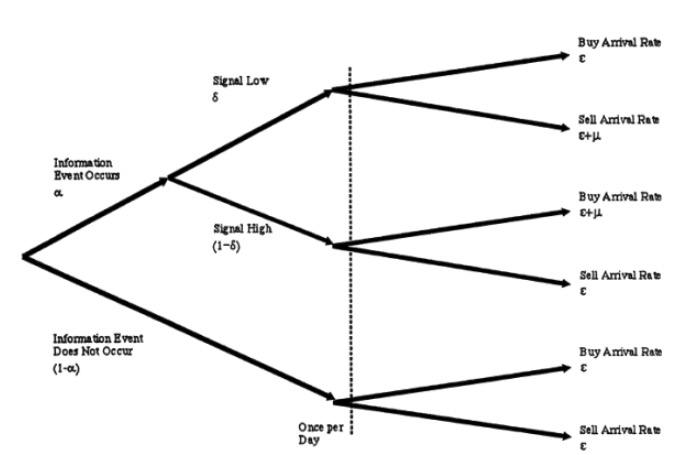
• #### 3 Atualização de transações e preços

Sabemos que os comerciantes de mercado são geralmente as grandes empresas que fazem isso. Eles são muito inteligentes e, durante a longa luta contra a TI e a TI, eles resumiram todos os parâmetros do modelo no gráfico em árvore acima, com uma grande quantidade de análise de dados históricos. Mas, felizmente, eles não são tão inteligentes quanto os comerciantes, e quando um dia de negociação está prestes a começar, eles não sabem como os comerciantes, se algo importante aconteceu hoje.

Agora, vamos experimentar o papel de um MM, lutando contra a TI e a UT. Em algum momento em t, nós nos marcamos como um vetor sobre a probabilidade de acontecer nada, algo bom, e algo ruim.

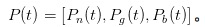。 É óbvio que no início do dia, ou seja, no dia em que /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, eu não vi um único alerta, então tudo o que eu posso dizer é que a probabilidade de nada acontecer é α, a probabilidade de algo bom acontecer é /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, e a probabilidade de algo ruim acontecer é /upload/asset/87418f07b12fce65f4c3f70b0e2494d2e19f769a.png.

Como é que devemos atualizar essa probabilidade? Bem, todos nós que fazemos escolhas de mercado conhecemos a fórmula de Bayes. Quando observamos uma venda, usamos a lei de Bayes para atualizar nossa própria estimativa de probabilidade.

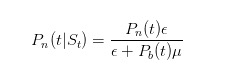
A molécula da fórmula diz que quando não há notícias, apenas os comerciantes ignorantes venderão com o valor de ε; e o divisor diz que, a qualquer momento, os comerciantes ignorantes venderão com o valor de ε, e os comerciantes informados venderão apenas com o valor de μ quando algo ruim acontecer.

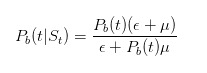
E também

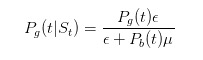
Antes de continuarmos com a inferência, vamos fazer alguns testes simples. Como já dissemos, se vemos um cartão de venda, então nossa estimativa da probabilidade de que algo ruim aconteça deve aumentar.

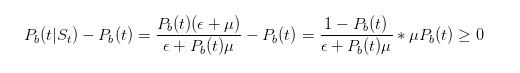
A partir daí, a nossa inferência confirma a nossa intuição.

Agora, com a probabilidade atualizada, podemos calcular o preço justo como o preço de compra que fazemos no mercado, expresso como

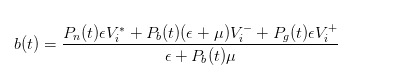
Por meio de uma dedução semelhante, podemos ver que, quando uma ordem de compra é enviada, o preço de venda que nós, como comerciantes, relatamos deveria ser

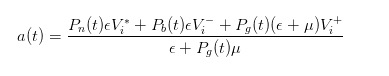
• #### 4 Expressão da diferença de preço após a transformação do preço

A expressão de preços de compra e venda acima não é intuitiva o suficiente, podemos introduzir o valor esperado do estoque no momento t para simplificar a expressão.

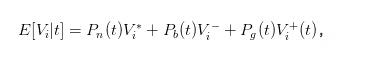
Assim, podemos transformar as expressões de bid e ask em

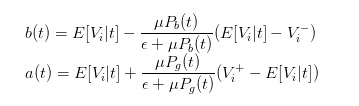
Assim, podemos expressar claramente a diferença de preço como

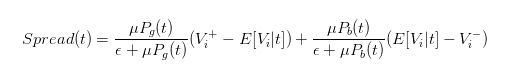
• #### 5 Efeitos do comportamento dos comerciantes sobre a diferença de preços

Com a expressão de diferença de preços, podemos analisar o impacto de diferentes comerciantes sobre a diferença de preços!

Quanto mais espinafre, menor é a diferença de preço. Note que ε é a taxa de chegada de comerciantes ignorantes (vamos chamar-lhes espinafre) e, se houver ε >> μ, podemos ver que, / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png Ambos os itens tendem a zero, o que significa que o spread também tende a zero. Sem salsinha, não há negociação. Se formos para o outro extremo, assumindo que não há salsinha no mercado, mas apenas um grupo de comerciantes mais bem informados do que o salsinha, então teremos a triste descoberta de que os preços que estamos pendurando serão 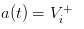e /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, então os comerciantes informados descobriram que não haverá lucro em comprar ou vender, o mercado necessariamente vai se afogar.

Veja, baseando-nos em algumas hipóteses, usando uma dedução matemática muito simples, conseguimos chegar a conclusões interessantes e profundas, e isso é provavelmente o grande charme dos modelos matemáticos. Depois de ler este artigo, eu também espero que vocês sejam gentis com as espinafres, que são a garantia de que o mercado pode negociar normalmente!

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.