m seguida, discutiremos a filtragem de dados. Mesmo se nos concentrarmos apenas em opções com data de vencimento de um mês, ainda precisamos filtrar alguns preços desatualizados, ou seja, preços de opções que tiveram volume de negociação zero nas últimas 24 horas. A liquidez também é uma questão fundamental para dados sobre contratos futuros com vencimento limitado, pois preços futuros desatualizados podem causar erros no cálculo do delta das opções. Portanto, preferimos usar a relação de paridade de compra e venda (PCP) para inferir o preço futuro correto em vez de usar o preço de mercado, como fazemos para contratos perpétuos muito líquidos. Se necessário, filtramos os preços médios das opções que violam a condição de não arbitragem proposta por Fengler (2009) e derivamos a volatilidade implícita dos preços restantes. Deve-se notar que a liquidez e a atividade de negociação das opções OTM são muito maiores do que as das opções ITM com o mesmo preço de exercício, então usamos a volatilidade implícita das opções de venda para calcular o caso de m < 1 e usamos a volatilidade implícita de opções de compra. A volatilidade é usada para calcular o caso em que m ≥ 1. É importante observar que a diferença entre a volatilidade implícita das opções de compra e venda do ATM é quase insignificante. Isso nos permite criar uma grade bruta a partir da superfície de volatilidade implícita do mercado e então interpolar para obter preços filtrados, conforme descrito abaixo.

Para obter uma série histórica contínua de cada preço de opção, construímos os preços de contratos sintéticos de expiração constante de determinada data de expiração e propriedades monetárias. As opções de curto prazo são representadas por um prazo fixo de 10 dias, o médio prazo é de 20 dias, enquanto para o longo prazo consideramos um prazo de 30 dias. Considerando que os preços do Bitcoin frequentemente sofrem mudanças de tendência, é impossível comparar o mesmo preço de exercício por um longo período de tempo, então também selecionamos uma gama apropriada de propriedades monetárias para interpolação. Encontramos amplo volume dentro de uma faixa de preço de exercício de cerca de 30% acima e abaixo dos níveis do Bitcoin. Portanto, interpolamos os preços das opções sintéticas para cada vencimento constante e propriedade monetária m∈{0,7,0,8,0,9,1,1,1,1,2,1,3} Nota 15. De fato, usamos o método de interpolação na superfície de volatilidade implícita sob o limite de não arbitragem proposto por Fengler (2009), que também propõe um método de interpolação de spline cúbica natural para suavizar a superfície de volatilidade implícita. No entanto, o formato da curva de volatilidade implícita do Bitcoin varia muito mais do que para outros tipos de opções, e descobrimos que a interpolação de spline cúbica é muito flexível e sensível a grandes intervalos entre certos preços de exercício. Portanto, usamos polinômios de Hermite cúbicos por partes que preservam a forma para interpolar a superfície de volatilidade implícita e verificar o preço posteriormente para garantir que a restrição de não arbitragem da convexidade em relação ao preço de exercício não seja violada. Essa técnica foi aplicada em muitos outros estudos acadêmicos, como Malz (1997) e Bliss e Panigirtzoglou (2002).

Primeiro, interpolamos a curva de sorriso de volatilidade implícita para obter volatilidade implícita de dinheiro constante sob a restrição de não arbitragem proposta por Fengler (2009) usando polinômios de Hermite cúbicos por partes que preservam a forma. Em seguida, obtemos a volatilidade implícita de opções de vencimento constante e dinheiro constante interpolando a estrutura a termo de volatilidade e usamos essa volatilidade implícita para criar preços de opções sintéticas (Nota 16). Para evitar quaisquer possibilidades de arbitragem de calendário, garantimos que a variação implícita total aumente com o aumento das datas de vencimento. Para avaliar o desempenho do hedge, também precisamos registrar o preço de cada opção sintética dentro de um incremento de tempo, sem alterar o straddle usado para construir a opção correspondente. Somente essa estrutura nos permite registrar os ganhos e perdas de um portfólio de hedge dinâmico. Portanto, criamos futuros e opções sintéticos usando os métodos descritos acima para obter preços atualizados de opções e liquidez com datas de vencimento de 9, 19 e 29 dias para o conjunto de dados diário. Da mesma forma, no conjunto de dados de 8 horas, construímos futuros e opções com datas de vencimento 8 horas menores que 10, 20 e 30 dias. No geral, geramos aproximadamente 175.000 preços de opções sintéticas de frequência diária e 88.000 taxas de hedge, e mais de 525.000 preços de opções sintéticas de frequência de 8 horas e mais de 263.000 taxas de hedge.

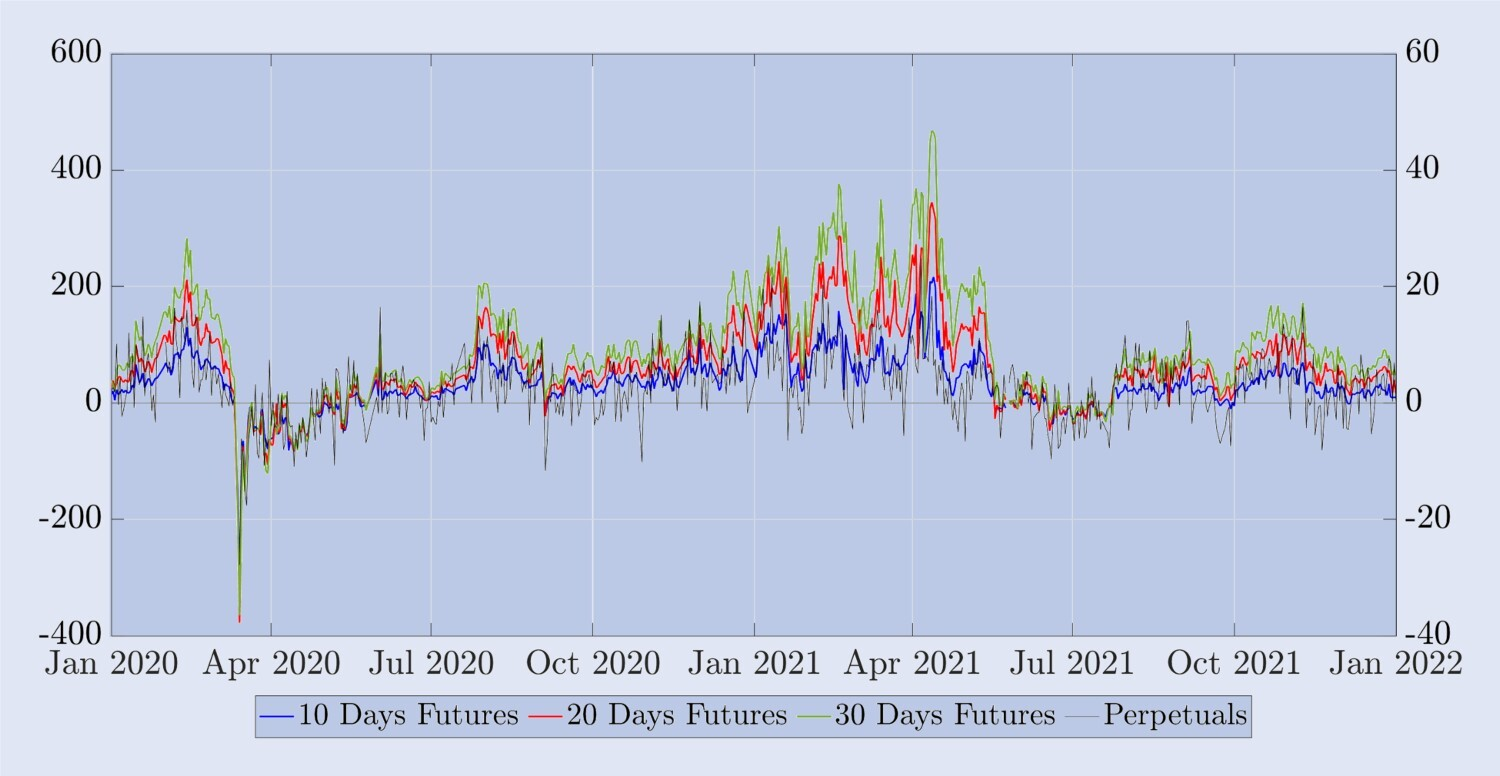
A seguir, examinaremos algumas características empíricas dos contratos perpétuos do Bitcoin e os compararemos com futuros de vencimento fixo antes de prosseguirmos para nosso estudo de hedge. O preço de liquidação das opções de Bitcoin não é um contrato negociável, então precisamos usar contratos futuros ou perpétuos como ferramentas de hedge. Nesse caso, a eficácia do uso de contratos futuros para proteger opções depende de fatores como a variabilidade da base. Para ilustrar essa variabilidade, a Figura 7 mostra a diferença entre o preço do mercado futuro (ou contrato perpétuo) e o índice BTC, dividido pelo índice BTC. Essa base percentual é expressa em pontos-base (bps), com a escala da esquerda sendo para os três futuros sintéticos de vencimento fixo e a escala da direita sendo a base relativa ao contrato perpétuo. Devido ao mecanismo de taxa de financiamento, o risco básico dos futuros perpétuos é muito baixo — menos de ±10 bps na maioria das vezes. Mas também é altamente volátil - por exemplo, durante a crise da COVID em março de 2020, a base perpétua atingiu quase -150 bps. Os contratos perpétuos têm muito pouco risco de base, o que sugere que eles podem fornecer uma ferramenta de proteção melhor do que os futuros de calendário com a mesma data de vencimento da opção. Diferentemente da base perpétua, a base para futuros com vencimento fixo é quase sempre positiva. Para futuros de 10 dias, a base pode chegar a 100 pontos-base, enquanto para futuros de prazo mais longo, a base pode chegar a 450 pontos-base. Além disso, como pode ser visto neste gráfico, as curvas de futuros de 10, 20 e 30 dias geralmente apresentam prêmio positivo - na verdade, a ordem é F30>F20>F10 em 620 dos 730 dias amostrados, e apenas em março de 2020. a ordem muda. A ação oposta ocorreu durante junho/abril (a queda da COVID e suas consequências) e junho/julho de 2021 (o fim da longa corrida de alta do Bitcoin).

Figura 7. Diferenças entre contratos spot, perpétuos e futuros.

O preço futuro menos o índice BTC, dividido pelo índice BTC, expresso em pontos-base. A escala da direita mede a porcentagem base para futuros perpétuos (preto), e a escala da esquerda mede a porcentagem base para futuros com datas de vencimento fixas de 10, 20 e 30 dias (azul, vermelho e verde, respectivamente). A amostra abrange um período de dois anos, começando em janeiro de 2020, com instantâneos diários tirados à meia-noite UTC.

Outro fator que afeta o sucesso de uma estratégia de arbitragem delta dinâmica são os custos de transação. Se o spread bid-ask do instrumento protegido for grande, o rebalanceamento frequente da arbitragem delta (no nosso caso, não apenas diariamente, mas a cada 8 horas) pode prejudicar o desempenho do hedge. No entanto, para qualquer opção dada, o delta não pode variar entre valores extremamente diferentes, por exemplo, uma opção de compra próxima de at-the-money sempre terá um delta próximo de 0,5, independentemente do modelo usado - veja Vähämaa (2004) para um exemplo. Portanto, diferentes valores de delta podem ter um impacto significativo no desempenho do hedge somente quando o spread bid-ask for grande. No entanto, os spreads de compra e venda em futuros perpétuos são apertados, e até mesmo os spreads de compra e venda em futuros calendário são apertados. Para futuros perpétuos, o spread entre compra e venda raramente excede um tick mínimo de US$ 0,50, o que equivale a 0,1 ponto-base a 0,25 ponto-base, dependendo do nível de preço. Os contratos futuros de calendário têm spreads de compra e venda ligeiramente maiores e aumentam com o aumento da data de vencimento, mas esses spreads também são muito pequenos em nossa amostra. Mesmo para os contratos futuros de vencimento mais longo, os spreads raramente excedem 5 pontos-base e ficam em torno de 1 ponto-base na maior parte do tempo. Uma dispersão tão baixa tem pouco impacto em nossas comparações entre diferentes valores de delta, então a ignoraremos na seguinte investigação empírica.

6. Pesquisa empírica de hedge

Inspirados em nossa discussão nas Seções 2, 3 e 5, tratamos opções inversas como opções de câmbio simples, ou seja, usamos o valor atual da opção subjacente para converter seu preço de Bitcoin em seu valor correspondente em USD. Escolhemos datas de vencimento fixas de 10, 20 e 30 dias para preços de opções e futuros sintéticos contínuos, e a liquidez das opções é escolhida entre 0,7 e 1,3. Nossos dados são construídos para hedges que são rebalanceados a cada 8 horas ou diariamente, e a amostra abrange um período de dois anos de 1º de janeiro de 2020 a 1º de janeiro de 2022, dividido em dois períodos de um ano. Amostras para mostrar os resultados. Em cada instante t, vendemos uma opção europeia com moeda m e data de vencimento T, e a protegemos com um contrato perpétuo ou contrato futuro com a mesma data de vencimento da opção. Os ganhos e perdas são registrados como erros de hedge em termos físicos, em da maneira usual – veja, por exemplo, Hull e White (2017). A volatilidade do mercado intradiário pode ser muito grande e os custos de transação do rebalanceamento são muito baixos, conforme discutido anteriormente. Portanto, definimos a frequência base da tabela de resultados para cada 8 horas. Também combinamos os rebalanceamentos de 8 horas com os horários de financiamento do contrato perpétuo, que são 00:00, 08:00 e 16:00 UTC. Isso ocorre porque o rebalanceamento usando contratos perpétuos para hedge também pode ser usado para lucrar com seus pagamentos de financiamento. Nota 17

Com exceção do delta HW, todos os deltas em (10) exigem que calculemos a inclinação da curva de volatilidade implícita ao rebalancear o portfólio de hedge. Investigamos várias técnicas numéricas para calcular a derivada da curva de volatilidade implícita e descobrimos que ajustar um polinômio cúbico é a abordagem mais simples e precisa. Com base nos valores de declive que calculamos numericamente, para cada opção, dependendo de sua liquidez e data de vencimento, aplicamos (10) para calcular o delta e o vega do BS usando a fórmula padrão do BS. Para o delta de Hull e White (2017), não imitamos seu período de calibração de 36 meses na amostra que eles usam em seu trabalho empírico sobre opções de índice de ações. Não há nem 36 meses de dados úteis disponíveis para opções de Bitcoin. Além disso, os preços do Bitcoin são muito mais voláteis do que o valor do S&P 500, e é por isso que gostaríamos de considerar fazer hedge várias vezes ao dia. Levando todos esses fatores em consideração, calibramos os parâmetros delta HW usando 30 janelas de observação na frequência diária e 90 janelas de observação na frequência de 8 horas. Nossos resultados comparam os erros de hedge usando contratos futuros de vencimento fixo e perpétuos e executam duas regressões HW dependendo do instrumento de hedge.

Apresentaremos nossos resultados usando um teste F padrão de diferenças de variância, usando o delta BS como referência, ou seja, o delta Sticky Strike (SS) de (10). Primeiro, a Tabela 2 apresenta os resultados do hedge de opções de 7, 1 e 3 dias com graus de moeda entre 10,20 e 30,0, onde cada opção é protegida com os futuros de vencimento fixo correspondentes e rebalanceada a cada 8 horas. equilíbrio. As entradas na tabela são taxas de variância, ou seja, a variância dos erros protegidos δadj em relação à variância dos erros protegidos delta BS.

Tabela 2. Resultados do teste F de hedge (rebalanceamento de 8 horas, futuros com data de vencimento fixa).

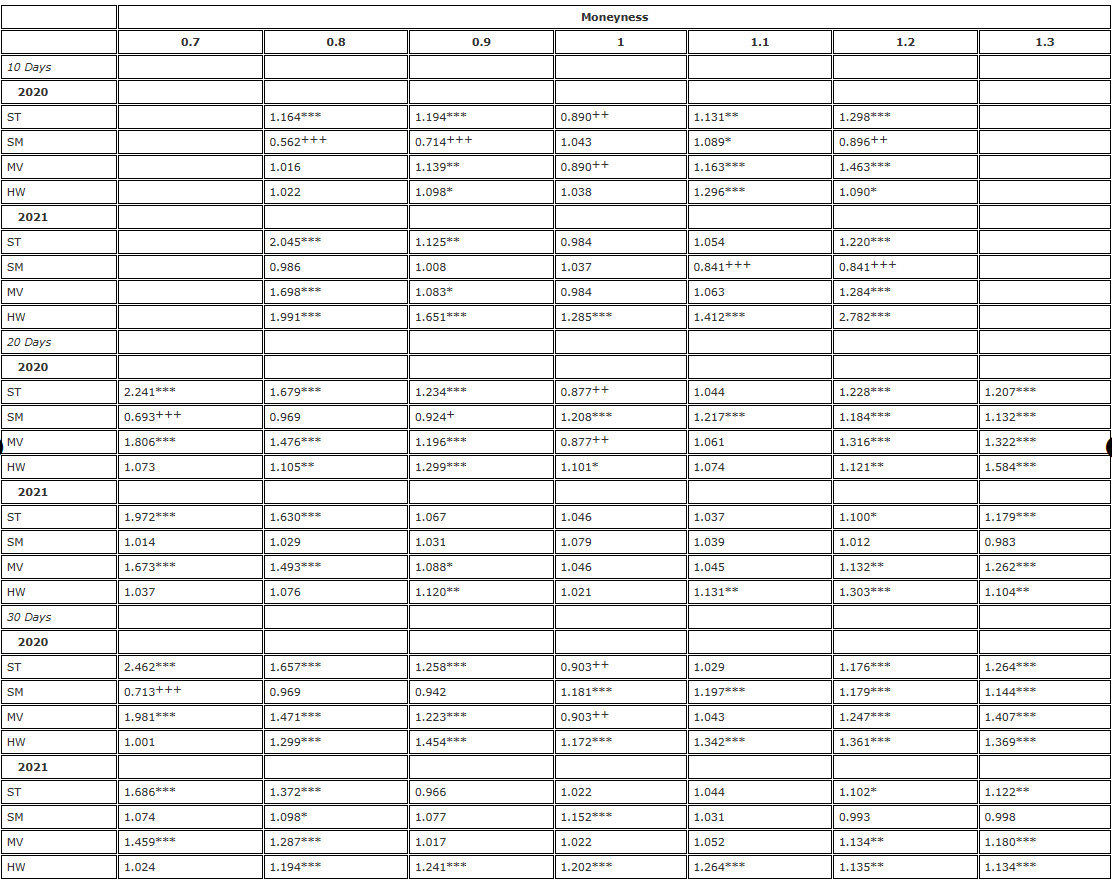
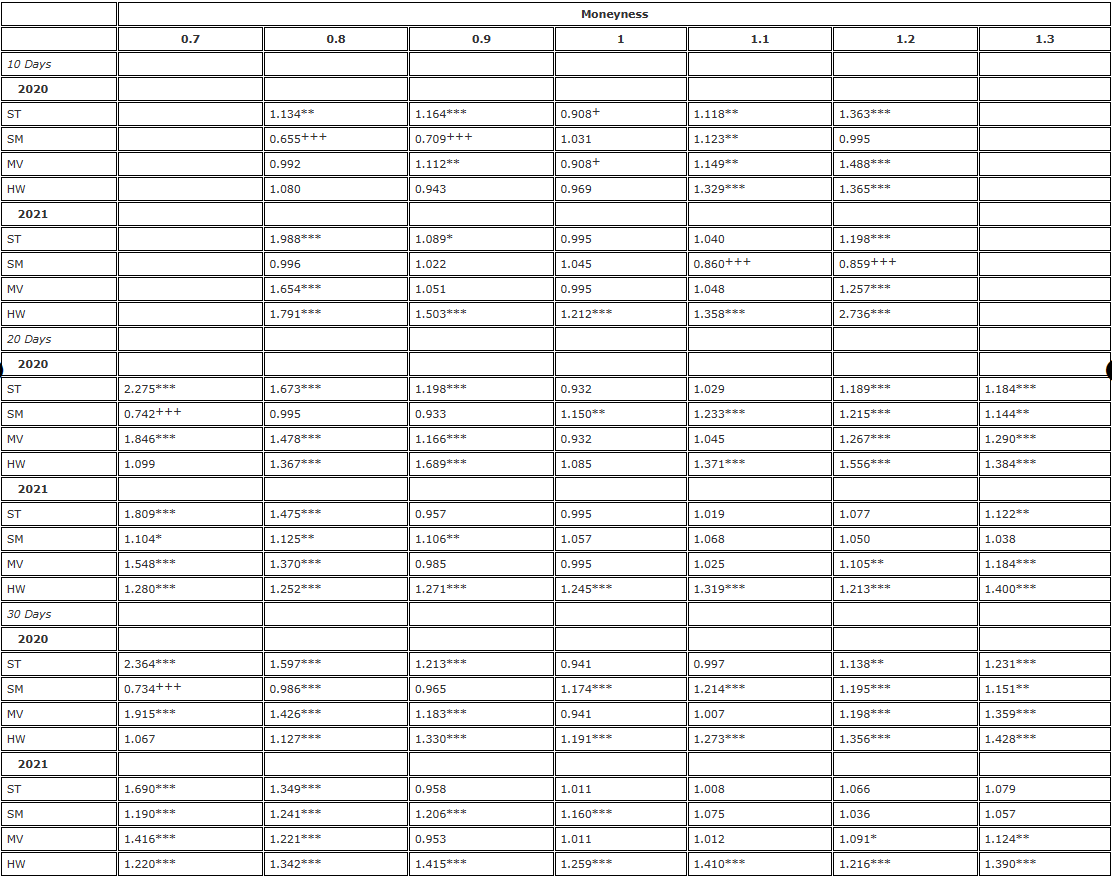
Nota: O nível de significância da razão de variância e do teste F unilateral são para a hipótese nula 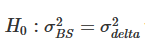e a hipótese alternativa /upload/asset/28dc6465a12c2e427a5ac.png, respectivamente. O hedge é baseado em um contrato futuro com a mesma data de vencimento da opção e é rebalanceado a cada 8 horas. Comparamos a variância dos erros de diferentes hedges delta em relação à variância do hedge usando delta BS e dividimos a amostra de dois anos em duas partes. Utilizamos opções de três vencimentos diferentes com moneyness variando de 0,7 a 1,3, usando opções de venda OTM quando moneyness <1 e opções de compra OTM quando moneyness >1. Para H∗, , e são usados ​​para representar os níveis de significância de 10%, 5% e 1%, respectivamente, e o mesmo é verdadeiro para H+.

Quanto maior a eficácia da proteção, menor a variância do erro de proteção, e o ganho de eficiência ao usar o delta da curva de sorriso ajustado é 1 menos essa taxa de variância. Por exemplo, ao proteger uma opção de 10 dias com um moneyness de 0,8, o delta SM (Smile Implied) produz uma taxa de variância de 0,562. Isso significa que o ganho de eficiência em comparação com a cobertura delta BS é de 1-0,562=43,8%, o que é muito significativo, então esta entrada é marcada como +++. Nas tabelas de razão de variância, os sobrescritos indicam a significância das razões de variância nos níveis de significância de 10%, 5% e 1% no teste F unilateral. Por exemplo,***Isso indica que a variância do erro de cobertura δadj é maior que a do erro de cobertura delta BS no nível de 1%. E ++ indica que a variância do erro de cobertura δadj é significativamente menor que o erro de cobertura delta BS no nível de 5%.

Primeiro, considere os resultados de 2020 na Tabela 2. Esta parte da amostra é caracterizada por aumentos de preços lentos, mas constantes, consistentes com o padrão de tendência constante de Derman (1999), onde esperaríamos que o delta SS (delta BS) fornecesse a proteção delta mais eficaz ou, no caso de um padrão de alcance limitado, SM delta para contabilizar a maioria dos deltas. Dominância. No geral, os resultados de 2020 na Tabela 2 mostram um padrão em que o sucesso de um delta específico superando uma proteção BS depende da liquidez da opção, e não do vencimento. Por exemplo, para opções at-the-money, o delta ST funciona melhor. Nota 18 Os ganhos de eficiência obtidos variam de 9,7% para a opção at-the-money de 30 dias a 12,3% para a opção de 20 dias e 11% para a opção de 10 dias. A direção relativa do desempenho dos deltas implícitos no smile (ou seja, SM) em comparação aos deltas ST e MV é oposta, não apenas para opções no dinheiro, mas também para todas as opções dentro do dinheiro. Ele supera o BS delta na proteção de opções de venda OTM, mas não para opções de compra OTM (exceto para a opção de compra de 10 dias com uma liquidez de 1,2). Para proteger opções de venda OTM profundas de 20 dias, o ganho de eficiência usando o delta implícito do smile (SM) ao longo de 2020 é de 1-0,693=30,7%, o que é muito significativo. Para opções de venda OTM profundas de 30 dias, o ganho de eficiência é de 28,7%, o que é quase o mesmo. Para outras opções de venda, os ganhos de eficiência do uso de hedge implícito em sorriso são muito menores, variando apenas de 3,1% a 7,6%.

Entretanto, para todas as outras opções, todos os deltas de sorriso ajustados têm desempenho inferior ao delta BS. No entanto, isso não é surpreendente, pois o preço do Bitcoin apresentou tendência constante durante grande parte de 2020. A taxa de hedge HW real proposta por Hull e White (2017) e a cobertura de variância mínima (MV) de Lee (2001) também não melhoram o delta BS (exceto que para opções at-the-money, a cobertura MV é a mesma que ST cobertura). Uma grande desvantagem do HW delta é que ele usa regressão para estimar seus parâmetros, o que torna a suposição independente e identicamente distribuída inválida para um ativo como o Bitcoin, que é muito propenso a saltos de retorno. O impacto de qualquer salto permanecerá dentro da janela móvel por um longo tempo e, portanto, terá um grande impacto na taxa de hedge HW.

As Figuras 2 e 5 mostram que 2021 foi caracterizado por preços mais altos, maior volatilidade e um aumento nos níveis gerais de volatilidade, juntamente com uma curva de volatilidade implícita em forma de sorriso mais plana, mas ainda assimétrica. Ao longo de 2021, o preço do Bitcoin oscilou muito entre US\( 30.000 e quase US\) 70.000 e, como mostra a Figura 2, a curva do sorriso de 30 dias tornou-se relativamente plana no final desse período. Mas a curva plana do sorriso torna o componente-chave do delta ajustado, a inclinação da curva do sorriso, quase redundante. Portanto, não é de surpreender que, no segundo ano da nossa amostra, os deltas ajustados pela curva não forneçam uma melhoria significativa nas taxas de hedge BS padrão para todas as opções de 20 e 30 dias. No entanto, em 2021, a curva de sorriso de curtíssimo prazo de 10 dias exibiu algumas características estranhas, apresentando tendência de alta durante a fase de alta do preço do Bitcoin. É por isso que a cobertura delta Smile Implied (SM) de opções de compra fora do dinheiro de 10 dias mostra uma melhoria de eficiência muito significativa de 15,9% em comparação ao uso do delta BS.

Em seguida, as Tabelas 3 e 4 testam a robustez dos resultados da Tabela 2 de duas maneiras: primeiro, executando novamente a análise em uma frequência diária (Tabela 3) e, em seguida, usando contratos perpétuos em vez de futuros com o mesmo vencimento como instrumento de hedge. . Os resultados da Tabela 3 mostram um padrão semelhante aos da Tabela 2, exceto que são menos significativos no geral — mas isso não deve nos surpreender, pois agora há apenas 365, em vez de 1.095 observações por ano. Eles confirmam nossa conclusão da Tabela 2 de que nenhum delta ajustado da curva do sorriso pode melhorar o delta da BS em 2021. Em 2020, também vimos o mesmo padrão de desempenho em relação ao delta BS, ou seja, o delta ST superou o BS em opções ATM, mas agora há algumas evidências de que o delta HW supera as opções ATM e opções de venda OTM. Ele também superou o BS com uma moneyness de 0,9 – mas nenhuma dessas estatísticas de razão de variância foi estatisticamente significativa.

Tabela 3. Resultados do teste F de hedge (rebalanceamento diário, futuros com vencimento fixo).

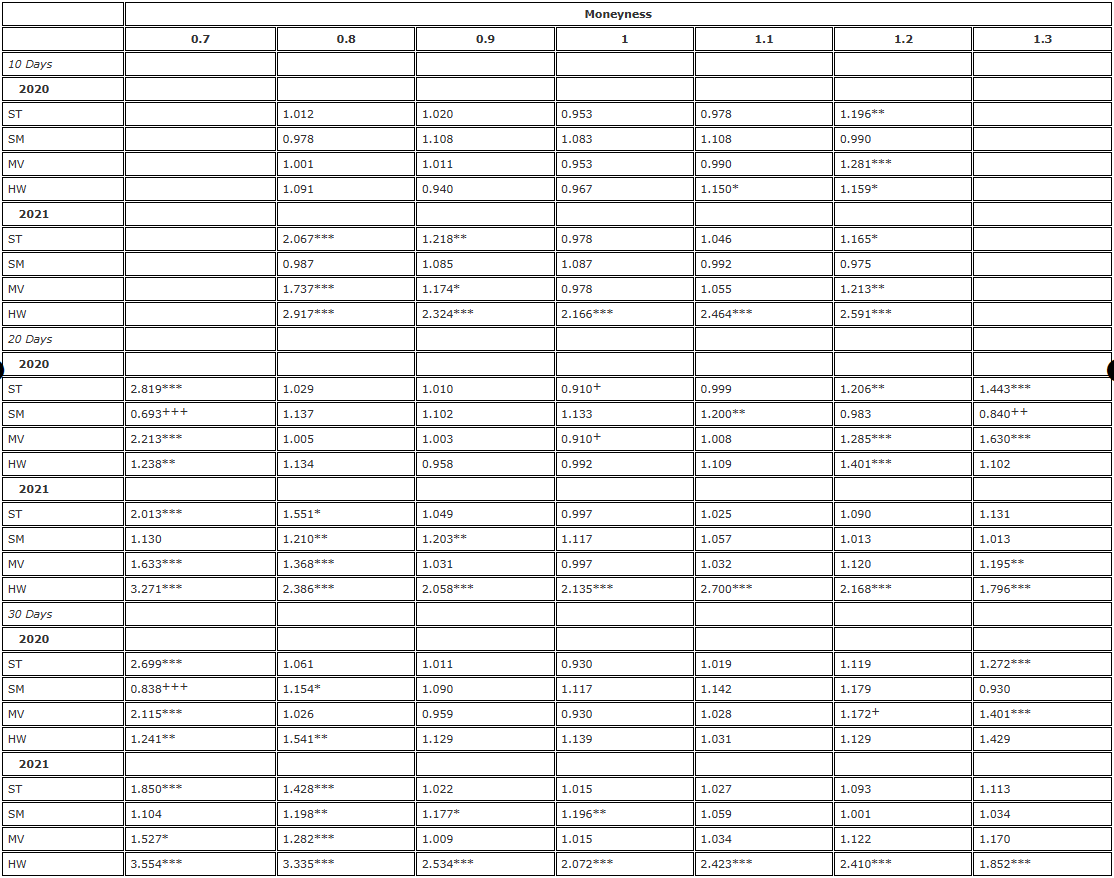
Nota: O nível de significância da razão de variância e do teste F unilateral são para a hipótese nula 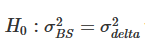e a hipótese alternativa /upload/asset/28dc6465a12c2e427a5ac.png, respectivamente. O hedge é baseado em um contrato futuro com a mesma data de vencimento da opção e é rebalanceado a cada 8 horas. Comparamos a variância dos erros de diferentes hedges delta em relação à variância do hedge usando delta BS e dividimos a amostra de dois anos em duas partes. Utilizamos opções de três vencimentos diferentes com moneyness variando de 0,7 a 1,3, usando opções de venda OTM quando moneyness <1 e opções de compra OTM quando moneyness >1. Para H∗, , e são usados ​​para representar os níveis de significância de 10%, 5% e 1%, respectivamente, e o mesmo é verdadeiro para H+.

Tabela 4. Resultados do teste F de hedge (rebalanceamento de 8 horas, contrato perpétuo).

Nota: O nível de significância da razão de variância e do teste F unilateral são para a hipótese nula 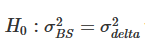e a hipótese alternativa /upload/asset/28dc6465a12c2e427a5ac.png, respectivamente. O hedge é baseado em um contrato futuro com a mesma data de vencimento da opção e é rebalanceado a cada 8 horas. Comparamos a variância dos erros de diferentes hedges delta em relação à variância do hedge usando delta BS e dividimos a amostra de dois anos em duas partes. Utilizamos opções de três vencimentos diferentes com moneyness variando de 0,7 a 1,3, usando opções de venda OTM quando moneyness <1 e opções de compra OTM quando moneyness >1. Para H∗, , e são usados ​​para representar os níveis de significância de 10%, 5% e 1%, respectivamente, e o mesmo é verdadeiro para H+.

A Tabela 4 é exatamente igual à Tabela 2, usando uma frequência de rebalanceamento de 8 horas para análise, mas usando contratos perpétuos como instrumentos de hedge para todas as opções. Observamos exatamente o mesmo padrão de desempenho inferior do delta BS como na Tabela 2, com ganhos de eficiência muito significativos para proteger puts OTM usando deltas ST/MV com delta implícito em smile (ou seja, SM) e opções ATM. Com exceção do hedge delta implícito da Curva Sorridente (SM), que mais uma vez proporcionou um ganho de eficiência grande e significativo para hedge de opções de compra OTM de 10 dias, nenhum delta ajustado da Curva Sorridente foi capaz de superar significativamente o delta BS em 2021. Para opções de ATM, também há alguns pequenos ganhos de eficiência (%) usando o delta ST/MV, e as taxas de variância na Tabela 4 são quase sempre menores do que aquelas na Tabela 2.

Essa descoberta nos leva a perguntar: os contratos perpétuos oferecem uma ferramenta de proteção melhor do que os futuros com o mesmo vencimento das opções? Para responder a essa pergunta, analisamos a taxa de variância, onde o numerador é a variância do erro de hedge perpétuo e o denominador é a variância do erro de hedge futuro. Novamente dividimos a amostra em dois períodos de um ano e apresentamos os resultados por delta (agora incluindo o delta BS) e opção, e a Tabela 5 mostra os resultados. Na tabela, uma taxa de variância menor que (maior que) 1 indica que um melhor (pior) efeito de hedge pode ser alcançado usando contratos perpétuos. A significância da estatística F depende se o swap perpétuo fornece uma ferramenta de hedge melhor (+) ou pior (-) do que os futuros do mesmo vencimento.*). É claro que o resultado depende pouco do valor monetário da opção, mas mais da data de vencimento da opção e das condições de mercado naquele momento. Para opções de 10 dias, as taxas de compra OTM são geralmente menores que 1. Para opções de 20 e 30 dias, a proteção com opções perpétuas pode apresentar algumas melhorias muito significativas, especialmente em 2021.

Tabela 5. Teste F comparando swaps futuros e perpétuos (rebalanceamento a cada 8 horas).

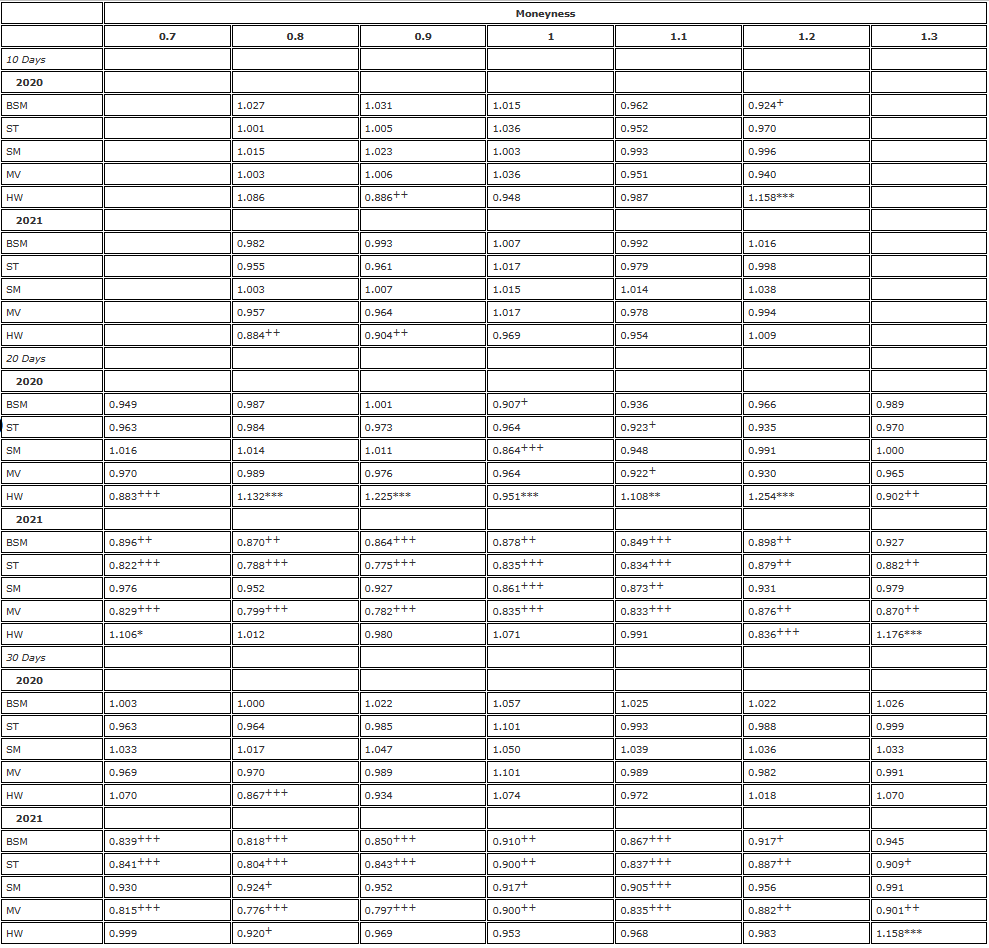
Nota: O nível de significância da razão de variância e do teste F unilateral são para a hipótese nula 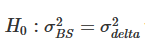e a hipótese alternativa /upload/asset/28dc6465a12c2e427a5ac.png, respectivamente. O hedge é baseado em um contrato futuro com a mesma data de vencimento da opção e é rebalanceado a cada 8 horas. Comparamos a variância dos erros de diferentes hedges delta em relação à variância do hedge usando delta BS e dividimos a amostra de dois anos em duas partes. Utilizamos opções de três vencimentos diferentes com moneyness variando de 0,7 a 1,3, usando opções de venda OTM quando moneyness <1 e opções de compra OTM quando moneyness >1. Para H∗, , e são usados ​​para representar os níveis de significância de 10%, 5% e 1%, respectivamente, e o mesmo é verdadeiro para H+.

Embora a tabela resultante forneça a eficiência relativa geral do delta em relação a diferentes ajustes da curva sorridente, nossa amostra de dois anos abrange uma ampla gama de regimes de mercado. Conforme mostrado na Figura 5, o mercado de Bitcoin oscila rapidamente entre tendências estáveis, flutuações de intervalo e quedas e picos acentuados. Portanto, para ajudar a entender qual delta tem melhor desempenho em quais estados de mercado, a Figura 8 descreve a série temporal da razão de variância, que é a variância do erro de hedge delta ajustado da curva sorridente dividida pela variância do erro de hedge delta BS. Isso está reequilibrando a cobertura a cada 8 horas, e agora cada variação é calculada usando apenas as 90 observações mais recentes — a mesma janela usada para a estimativa do parâmetro delta HW. Ressaltamos que valores maiores que 1 indicam desempenho de hedge ruim do delta ajustado pelo sorriso em relação ao delta do BS. Para maior clareza, apresentamos os resultados em uma escala logarítmica, portanto, nessas figuras, uma razão de variância de 1 é representada por zero . . Qualquer linha abaixo de zero indica que o delta melhora em relação ao delta BS, mas uma linha acima de zero mostra que o delta fornece uma proteção menos eficaz do que o BS.

Figura 8. Desempenho de hedge da amostra rolante. (a) resultados de opções de 10 dias e (b) resultados de opções de 30 dias.

A taxa de variância mostra o desempenho de várias taxas de hedge de opções perpétuas em relação ao delta BS usando o rebalanceamento de 8 horas, onde a variância do erro de hedge é calculada usando as primeiras 90 observações. Apresentamos os resultados do logaritmo para (a) opções de 10 dias e (b) opções de 30 dias em uma amostra de dois anos. A linha contínua 0 é um valor de referência, uma proporção maior que 0 indica um desempenho pior em relação ao BS, e uma proporção menor que 0 indica um desempenho melhor em relação ao BS. A figura (a) acima descreve o desempenho de uma opção de venda OTM com m=0,8, enquanto o gráfico superior em (b) mostra o desempenho de uma opção de venda OTM com m=0,7. O gráfico do meio mostra o desempenho de (a) e (b). O desempenho das opções ATM é mostrado abaixo para opções de compra OTM com (a) moneyness de 1,2 e (b) moneyness de 1,3.

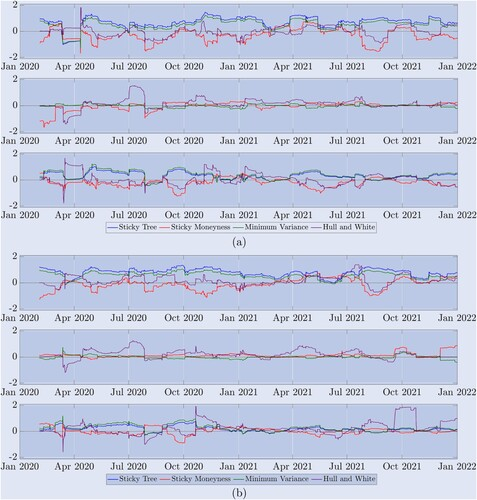
Os três gráficos superiores (a) mostram os resultados para opções de 10 dias, e os três gráficos inferiores (b) mostram os resultados para opções de 30 dias. Em cada caso (a) e (b), os gráficos acima são para opções de venda OTM. Esses gráficos confirmam os resultados da Tabela 2: deltas de ST (azul) e MV (verde) tiveram desempenho inferior ao longo de quase todo o período. , são menores do que BS; de acordo com as expectativas de classificação de mercado de Derman (1999), o delta SM supera o delta BS durante os períodos em que o mercado está limitado a uma faixa, mas quando o mercado está em tendência, como o primeiro período começando em janeiro de 2021, durante o segundo corrida de touros e a segunda corrida de touros mais tarde naquele ano, o delta SM não teve um desempenho tão bom quanto o delta BS; enquanto o delta HW teve um desempenho diferente. O gráfico do meio em cada conjunto de gráficos mostra a taxa de variância para as opções ATM protegidas. Neste caso, todos os deltas ajustados ao sorriso são muito semelhantes, já que a curva do sorriso do Bitcoin é geralmente (mas nem sempre) muito plana neste ponto. O gráfico inferior em cada conjunto de gráficos mostra o desempenho de diferentes deltas para proteção de opções de compra OTM. Novamente, o SM delta parece ser a melhor opção, mas está disponível apenas para opções de 10 dias e não é uma melhoria tão grande em relação ao BS quanto o OTM sugere. Para opções de 30 dias, nenhum delta conseguiu melhorar consistentemente o BS, especialmente durante 2021.

7. Conclusão

Estudos empíricos acadêmicos anteriores examinaram apenas a cobertura delta com curva de sorriso implícita sem modelo e curva de sorriso dependente da instituição ajustada para opções de índice de ações. Embora os resultados sejam mistos, a conclusão geral é que uma taxa de hedge ajustada pela curva sorridente só pode melhorar o desempenho do delta de Black-Scholes para opções de venda fora do dinheiro em certas circunstâncias. Mas demonstramos que a curva de sorriso de volatilidade implícita do Bitcoin se comporta de forma muito diferente das opções de índice de ações, por isso é de grande interesse estudar a eficácia da taxa de hedge ajustada pela curva de sorriso que os profissionais geralmente preferem.

Incentivamos o uso de vários usos potenciais do delta ajustado, a maioria dos quais depende exclusivamente da relação entre a curva de volatilidade implícita da opção de hedge e o tempo até o vencimento. Ao usar um conjunto de dados exclusivo sobre opções do Deribit, podemos comparar o desempenho de hedge das opções de Bitcoin mais ativas na bolsa Deribit, ou seja, opções com preços de exercício 30% acima e abaixo do índice BTC atual e tempos de expiração de até um mês. Analisamos a variância dos erros de hedge delta, onde o instrumento de hedge pode ser um contrato futuro com a mesma data de vencimento da opção ou um contrato perpétuo - um produto inovador exclusivo do mercado de derivativos de criptomoedas. Ao rebalancear o hedge a cada oito horas (coincidindo com o tempo de financiamento do contrato perpétuo) ou diariamente, e usar contratos futuros ou contratos perpétuos com o mesmo tempo de expiração do instrumento de hedge, obtemos alguns resultados muito robustos. Além disso, em vez de simplesmente tabular os erros quadráticos médios de diferentes taxas de hedge, como feito por Coleman et al. (2001), Vähämaa (2004), Alexander et al. (2012) e muitos outros, aplicamos um teste de razão de variância simples que fornece a significância estatística do ganho de eficiência do uso de um determinado delta em relação ao delta BS.

Usando esta abordagem, demonstramos que para opções fora do dinheiro, o delta implícito na curva sorridente (dinheiro rígido) é significativamente melhor do que o delta de Black-Scholes padrão em hedge, em alguns casos em mais de 40% mais eficientemente . O delta de variância mínima também supera o delta BS, mas apenas para opções dentro do dinheiro, pois coincide com o delta da árvore pegajosa. Nenhum outro delta ajustado pela curva do sorriso melhorou consistentemente o delta BS, e até mesmo as proteções delta implícitas pelo sorriso e de variância mínima tiveram desempenho ruim durante grande parte de 2021. A única exceção é o hedge implícito do sorriso em opções de compra de curto prazo fora do dinheiro quando a inclinação da curva de volatilidade implícita se torna positiva. Comparado a índices de ações como o S&P 500, os preços do Bitcoin não flutuam para cima de forma constante e então caem repentinamente - seus aumentos de preço podem ser tão grandes quanto suas diminuições de preço, então sua curva de sorriso pode ser muito simétrica ou até mesmo completamente inclinada para cima. . Também demonstramos que contratos perpétuos são melhores instrumentos de hedge do que futuros com o mesmo vencimento das opções, independentemente do valor monetário das opções. Isso é particularmente evidente em opções de prazo mais longo, onde a base entre contratos perpétuos e futuros é maior.

Nossa pesquisa se concentra em estruturas robustas sem modelos, que também são a escolha preferida de muitos profissionais. Não consideramos a cobertura usando quaisquer modelos estocásticos paramétricos e/ou de volatilidade local pela simples razão de que a invariância de escala desses processos significa que o delta é efetivamente livre de modelo e, portanto, coincide com o delta implícito no sorriso usado neste estudo. Como introduzimos o delta de variância mínima robusto de Lee (2001) em nosso estudo, acreditamos que adicionar diferentes processos de volatilidade estocástica para hedge de delta dinâmico é uma questão de pesquisa menos relevante para o atual setor de negociação de criptomoedas.

Este artigo se concentra na cobertura dinâmica de delta com rebalanceamento frequente, o que pode ajudar os formadores de mercado em opções de Bitcoin a obter uma vantagem competitiva em um mercado que só está realmente começando a amadurecer em 2021. No entanto, o mercado de Bitcoin cresceu tão rapidamente que grandes traders profissionais como Jump Trading, Jane Street, XBTO e Cumberland DRW estão negociando opções de Bitcoin, geralmente com volumes diários superiores a US$ 1 bilhão. Muitas novas opções de expiração e tamanhos de contratos de opções também estão sendo introduzidos para atender à demanda. Por exemplo, a CME lançou recentemente opções de micro Bitcoin para comerciantes de varejo. Apesar disso, o spread de compra e venda das opções de Bitcoin ainda é relativamente grande, muito maior do que o dos contratos futuros ou perpétuos de Bitcoin. Portanto, a lucratividade da criação de mercado no mercado de opções de Bitcoin depende mais da cobertura delta dinâmica precisa do que da cobertura delta-gama-vega. Se o spread de compra e venda das opções de Bitcoin diminuir no futuro, pode ser interessante estudar o hedge gama e vega do livro de opções de Bitcoin. Entretanto, no momento em que este artigo foi escrito, os custos de transação do uso de opções para proteger o preço e o risco de volatilidade podem corroer quaisquer lucros adicionais que poderiam ser obtidos por meio de spreads mais baixos.

declaração

Somos gratos aos revisores anônimos cujos comentários melhoraram significativamente o artigo.

Declaração de Divulgação

Os autores declaram não haver conflitos de interesse.

Notas

1. Em contraste, os deltas derivados de modelos não invariantes de escala, como o modelo de volatilidade local de Dupire (1994) ou o modelo de árvore pegajosa de Derman e Kани (1994), não são teoricamente equivalentes aos deltas invariantes de escala. O Delta de variância mínima também não é um Delta invariante de escala; é a derivada total que inclui o efeito Vega de correlações de volatilidade de preço diferentes de zero.

2. Por exemplo, veja o recenteArtigos CAIA, outro artigo sobre o meioartigo,assim como risklatte e stackexchange E vários fóruns de finanças quantitativas.

3. Nesta literatura, Nastasi et al. (2020) calibram um modelo de consistência de sorriso para opções de commodities para capturar a dinâmica do sorriso, enquanto Malz (2000) explica como levar em consideração os ajustes de sorriso ao medir o risco de opções de câmbio estrangeiro. Por dentro.

4. As opções do Deribit têm vencimentos bidiários, quinzenais, bimestrais e trimestrais, e podem durar até 9 ou 12 meses. Seu ativo subjacente é o “Deribit BTC Index” (BTC), que é uma média ponderada igualmente dos últimos preços do Bitcoin em 11 exchanges, excluindo os preços mais altos e mais baixos. Os 9 preços restantes são usados ​​para calcular o índice. Atualmente, essas exchanges incluem Binance, Bitfinex, Bitstamp, Bittrex, Coinbase Pro, Gemini, Huobi Global, Itbit, Kraken, LMAX Digital e OKEx, e o índice é atualizado a cada segundo. Há mais datas de vencimento de opções do que datas de vencimento de futuros, então, para que a Deribit liste os preços das opções para Bitcoin e USD, eles usam os mesmos preços futuros (possivelmente sintéticos) das datas de vencimento das opções. Isso não significa que o contrato futuro (possivelmente sintético) seja o subjacente. Na verdade,Especificações das opções do Deribit É claramente declarado que o ativo subjacente é o Deribit BTC Index. Para opções de curto prazo, o intervalo de exercício varia de 50% a 150% do preço atual do BTC, e para opções com vencimentos superiores a 6 meses, o intervalo de exercício pode ser de até 800% do preço atual do BTC.

5. Veja tambémDados históricos de opções do CBOE, para entender o volume de negociação de opções SPX na CBOE.

6. Veja tambémVolume de negociação de opções de Bitcoine Opções de Bitcoin do Goldman Sachs。

7. Em seguida vem CME (5%), depois OKEx (2,5%), assim como FTX e Bit.com. Para detalhes, consulteThe Block Options。

8. Para calcular o retorno final, a Deribit usa o índice BTC médio 30 minutos antes do vencimento como valor de liquidação. Para detalhes, veja o oficialEspecificações das opções do Deribit . É importante observar que o mercado de opções de Bitcoin da Deribit não está completo. Os índices em si não são negociáveis ​​e exigem replicação cara e rebalanceamento frequente. O mercado está incompleto para os traders devido à falta de informações sobre o cálculo preciso do valor de liquidação. Entretanto, uma discussão detalhada desta questão está além do escopo deste artigo, e nos referimos a Alexander et al. (2022a) para uma discussão aprofundada.

9. Consulte 2022Mercado descentralizado de criptomoedas Classificação.

10. Futuros inversos são contratos futuros denominados em Bitcoin com base no preço do Bitcoin em USD ou no valor de um índice de Bitcoin. Tanto os futuros padrão quanto os inversos usam o valor do USD como subjacente, mas diferem no método de liquidação: os futuros padrão da CME têm um valor nocional de 0,1 ou 5 bitcoins e são pagos em USD, enquanto o valor nocional dos futuros inversos é de US\( 1 ou US\) 10. , e pagável em Bitcoin. Por outro lado, esse mecanismo de pagamento leva a um cálculo diferente de lucros e perdas (PnL). Para futuros padrão, você precisa subtrair o preço de fechamento do preço de abertura do futuro e multiplicar o resultado pelo valor nominal para obter o lucro ou prejuízo em dólares americanos. Futuros inversos (e opções) têm um procedimento de liquidação diferente, que pega o inverso do preço de abertura menos o inverso do preço de fechamento e, então, multiplica o resultado pelo valor nominal da posição para obter o lucro ou prejuízo medido em Bitcoin. O “preço de abertura” e o “preço de fechamento” aqui se referem ao valor em dólares do contrato futuro no momento de entrada e saída da posição.

11. Veja tambémTaxa de Financiamento Perpétuo Deribit, para uma descrição do cálculo da taxa de financiamento do Deribit.

12. Veja tambémThe BlockouCoinglass. É importante observar que mais de oito bolsas apresentaram volumes de negociação anormalmente altos. No entanto, ignoramos as muitas bolsas que inflaram artificialmente os volumes devido à lavagem de negociações.

13. Essa aproximação também foi defendida por Coleman et al. (2001) e muitos outros.

14. Derman (1999) chamou o modelo SS de uma “tentativa do pobre” de replicar o modelo BS usando uma árvore de volatilidade implícita.

15. Com exceção de puts (m=0,7) e calls (m=1,3) muito profundas e fora do dinheiro, essas opções são subnegociadas na categoria de vencimento de curto prazo. Só conseguimos calcular preços sintéticos 75% das vezes, então excluímos essas opções dos nossos resultados finais.

16. É claro que o valor de PCP para cada nível de exercício será diferente. Como a negociação geralmente se concentra em opções ATM, é difícil encontrar um nível de exercício ITM/OTM em que tanto calls quanto puts sejam negociados ativamente, então usamos o valor PCP derivado do cálculo retroativo de opções ATM. Interpolamos os valores do ATM PCP para duas datas de vencimento adjacentes e usamos esses valores para obter preços de opções fixas sintéticas quando necessário.

17. Por exemplo, como sempre mantemos um contrato perpétuo em nossa construção, o hedger precisa pagar o financiamento quando a base do contrato perpétuo é positiva e recebe o financiamento quando a base é negativa. O oposto é verdadeiro para proteger posições longas de opções. De qualquer forma, na Figura 7 podemos ver que a base do contrato perpétuo está mudando, às vezes positiva e às vezes negativa. Não é difícil escrever um algoritmo de hedge para sair completamente de uma posição protegida antes que o financiamento expire, mas ele não sairá se a posição protegida receber financiamento. Esse tipo de “estratégia de taxa de financiamento” é muito comum entre fundos de hedge hoje em dia, em mercados onde não há regulamentações para impedir que esses robôs de negociação estratégica operem. Em qualquer caso, estamos apenas sugerindo adicionar estratégias de financiamento às estratégias de hedge e não estamos explorando potenciais lucros ou perdas, pois este não é um estudo de estratégias de negociação de alta frequência.

18. Para opções ATM, os deltas ST e MV são os mesmos, então os resultados são os mesmos, mas apenas neste caso.

Referências

1. Alexander, C., Pricing, Hedging and Trading Financial Instruments. Market Risk Analysis III, 2008 (Wiley). [Google Scholar]

2. Alexander, C. and Nogueira, L., Model-free hedge ratios and scale invariant models. J. Bank. Finance, 2007a, 31, 1839–1861. [Crossref], [Web of Science ®], [Google Scholar]

3. Alexander, C. and Nogueira, L., Model-free price hedge ratios for homogeneous claims on tradable assets. Quant. Finance, 2007b, 7(5), 473–479. [Taylor & Francis Online], [Web of Science ®], [Google Scholar]

4. Alexander, C., Rubinov, A., Kalepky, M. and Leontsinis, S., Regime-dependent smile-adjusted delta hedging. J. Futures Mark., 2012, 32(3), 203–229. [Crossref], [Web of Science ®], [Google Scholar]

5. Alexander, C., Chen, D. and Imeraj, A., Inverse and quanto inverse options in a Black–Scholes world. SSRN Working Paper, 2022a. [Crossref], [Google Scholar]

6. Alexander, C., Deng, J., Feng, J. and Wan, H., Net buying pressure and the information in bitcoin option trades. J. Financ. Mark., 2022b. (Article in Press). [Crossref], [Google Scholar]

7. Attie, L., The performance of smile-implied delta hedging. Canadian Derivatives Institute, Technical Note TN 17-01, 2017. [Google Scholar]

8. Bakshi, G., Cao, C. and Chen, Z., Empirical performance of alternative option pricing models. J. Finance, 1997, 52, 2003–2049. [Crossref], [Web of Science ®], [Google Scholar]

9. Bates, D., Hedging the smirk. Finance Res. Lett., 2005, 2(4), 195–200. [Crossref], [Google Scholar]

10. Black, F. and Scholes, M., The pricing of options and corporate liabilities. J. Polit. Econ., 1973, 81(3), 637–654. [Crossref], [Web of Science ®], [Google Scholar]

11. Bliss, R. and Panigirtzoglou, N., Testing the stability of implied probability density functions. J. Bank. Finance, 2002, 26(2-3), 381–422. [Crossref], [Web of Science ®], [Google Scholar]

12. Chen, K. and Huang, Y., Detecting jump risk and jump-diffusion model for bitcoin options pricing and hedging. Math., 2021, 9(20), 2567. [Crossref], [Google Scholar]

13. Chi, Y. and Hao, W., Volatility models for cryptocurrencies and applications in the options market. J. Int. Financ. Mark I., 2021, 75, 101421. [Crossref], [Google Scholar]

14. Coleman, T., Kim, Y., Li, Y. and Verma, A., Dynamic hedging with deterministic local volatility function model. J. Risk, 2001, 4(1), 63–89. [Taylor & Francis Online], [Google Scholar]

15. CryptoCompare, Exchange review. September 2022, 2022. [Google Scholar]

16. Crépey, S., Delta-hedging vega risk?. Quant. Finance, 2004, 4(5), 559–579. [[Taylor & Francis Online]](https://www.tandfonline.com/servlet/linkout?suffix=CIT0016&dbid=20&doi=10.1080%2F14697688.2023.2181205&key=10.1080%2F14697680400008718&tollfreelink