Uma ferramenta poderosa para traders programáticos: algoritmo de atualização incremental para calcular a média e a variância

Introdução

Em negociação programática, muitas vezes é necessário calcular médias e variações, como o cálculo de médias móveis e indicadores de volatilidade. Quando precisamos de cálculos de alta frequência e de longo prazo, é necessário reter dados históricos por um longo tempo, o que é desnecessário e que consome recursos.

Média simples e variância

Se usarmos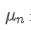para representar o valor médio do n-ésimo ponto de dados, assumindo que já tenhamos calculado a média de n-1 pontos de dados /upload/asset/28e28ae0beba5e8a810a6.png, agora recebemos um novo ponto de dados /upload/asset/28d4723cf4cab1cf78f50.png. Queremos calcular o novo número médio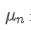A seguir está uma derivação pormenorizada.

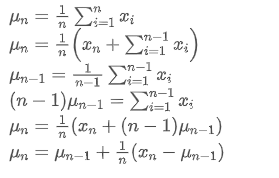
O processo de atualização da variância pode ser dividido nas seguintes etapas:

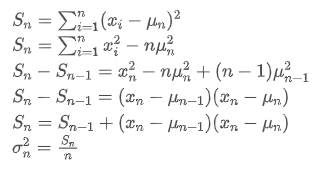
Como pode ser visto a partir das duas fórmulas acima, este processo permite-nos atualizar novas médias e variações ao receber cada novo ponto de dados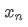Observando a atualização média acima mostra que a quantidade de novas atualizações médias é um desvio entre novos dados e médias passadas multiplicado por uma razão. Se esta razão for fixa, ela levará a uma média ponderada exponencialmente, que discutiremos em seguida.

Média ponderada exponencialmente

A média ponderada exponencial pode ser definida pela seguinte relação recursiva:

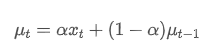
Entre eles,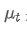é a média ponderada exponencial no momento t,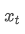é o valor observado no momento t, α é o fator de peso e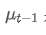é a média ponderada exponencial do ponto de tempo anterior.

Variança ponderada exponencialmente

Em relação à variância, precisamos calcular a média ponderada exponencial dos desvios quadrados em cada ponto de tempo.

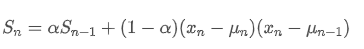
Entre eles,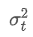é a variância ponderada exponencial no momento t, e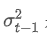é a variância ponderada exponencial do ponto de tempo anterior.

Observe a média ponderada exponencialmente e a variância, suas atualizações incrementais são intuitivas, mantendo uma parte dos valores passados e adicionando novas alterações.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA e EMA

A SMA (também conhecida como média aritmética) e a EMA são duas medidas estatísticas comuns, cada uma com características e usos diferentes. A primeira atribui peso igual a cada observação, refletindo a posição central do conjunto de dados. A última é um método de cálculo recursivo que dá maior peso a observações mais recentes. Os pesos diminuem exponencialmente à medida que a distância do tempo atual aumenta para cada observação.

• Distribuição do peso: A SMA atribui a mesma ponderação a cada ponto de dados, enquanto a EMA atribui uma maior ponderação aos pontos de dados mais recentes.
• Sensibilidade a novas informaçõesO SMA não é suficientemente sensível aos dados recém-adicionados, uma vez que implica o recalculo de todos os pontos de dados.
• Complexidade computacionalO cálculo da SMA é relativamente simples, mas à medida que o número de pontos de dados aumenta, o custo computacional também aumenta.

Método de conversão aproximado entre EMA e SMA

Embora a SMA e a EMA sejam conceitualmente diferentes, podemos fazer a EMA aproximar-se de uma SMA contendo um número específico de observações escolhendo um valor α apropriado.

O SMA é a média aritmética de todos os preços dentro de uma determinada janela de tempo.

o centróide da SMA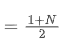

A EMA é um tipo de média ponderada em que os pontos de dados mais recentes têm maior peso.

o centróide da EMA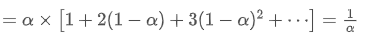

Quando assumimos que SMA e EMA têm o mesmo centróide, podemos obter:

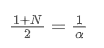
Para resolver esta equação, podemos obter a relação entre α e N.

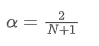
Isto significa que, para uma dada SMA de N dias, o valor α correspondente pode ser usado para calcular uma EMA equivalente, de modo que tenham o mesmo centroide e os resultados sejam muito semelhantes.

Conversão da EMA com diferentes frequências de atualização

Suponha que temos uma EMA que atualiza a cada segundo, com um fator de peso de /upload/asset/28da19ef219cae323a32f.png. Isso significa que a cada segundo, o novo ponto de dados será adicionado à EMA com um peso de /upload/asset/28da19ef219cae323a32f.png, enquanto a influência dos pontos de dados antigos será multiplicada por /upload/asset/28cfb008ac438a12e1127.png.

Se alterarmos a frequência de atualização, como atualizar uma vez a cada f segundos, queremos encontrar um novo fator de peso /upload/asset/28d2d28762e349a03c531.png, para que o impacto geral dos pontos de dados dentro de f segundos seja o mesmo que quando atualizado a cada segundo.

Dentro de f segundos, se nenhuma atualização for feita, o impacto dos pontos de dados antigos decadirá continuamente f vezes, cada vez multiplicado por /upload/asset/28e50eb9c37d5626d6691.png. Portanto, o fator de decadência total após f segundos é /upload/asset/28e296f97d8c8344a2ee6.png.

Para que a EMA atualizada a cada f segundos tenha o mesmo efeito de decaimento que a EMA atualizada a cada segundo dentro de um período de atualização, definimos o fator de decaimento total após f segundos igual ao fator de decaimento dentro de um período de atualização:

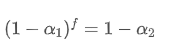
Resolvendo esta equação, obtemos novos fatores de peso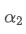

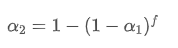
Esta fórmula fornece o valor aproximado do novo fator de peso /upload/asset/28d2d28762e349a03c531.png, que mantém o efeito de suavização da EMA inalterado quando a frequência de atualização muda.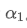com um valor de 0,001 e atualizado a cada 10 segundos, se for alterado para uma atualização a cada segundo, o valor equivalente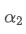seria aproximadamente 0,01.

Implementação de código Python

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Resumo

No comércio programático de alta frequência, o processamento rápido de dados em tempo real é crucial. Para melhorar a eficiência computacional e reduzir o consumo de recursos, este artigo introduz um algoritmo de atualização on-line para calcular continuamente a média ponderada e a variância de um fluxo de dados. As atualizações incrementais em tempo real também podem ser usadas para vários cálculos de dados estatísticos e indicadores, como a correlação entre dois preços de ativos, ajuste linear, etc., com grande potencial. A atualização incremental trata os dados como um sistema de sinais, o que é uma evolução no pensamento em comparação com cálculos de período fixo.