Na semana passada, apresentamosGestão de Risco VaRQuando falamos sobre o risco de um portfólio, ele não é igual ao risco de cada ativo individual, mas está relacionado à sua correlação de preços. Tomando dois ativos como exemplo, se a correlação positiva deles for muito forte, ou seja, eles sobem e descem juntos, então diversificar investimentos longos não reduzirá o risco. Se a correlação negativa for muito forte, a diversificação pode reduzir significativamente o risco. A pergunta natural é: ao investir em um portfólio, como maximizar os retornos com um certo nível de risco? É aqui que entra em jogo a teoria de Markowitz, que apresentarei hoje.

A Teoria Moderna de Portfólios (MPT), proposta por Harry Markowitz em 1952, é uma estrutura matemática para seleção de portfólios que visa maximizar os retornos esperados selecionando diferentes combinações de ativos de risco. lucros e, ao mesmo tempo, controlar os riscos. A ideia central é que os preços dos ativos não se movem em sincronia perfeita (ou seja, há uma correlação imperfeita entre os ativos) e o risco geral do investimento pode ser reduzido pela diversificação da alocação de ativos.

Conceitos-chave da teoria de Markowitz

1. Taxa de retorno esperada: Este é o retorno que um investidor pode esperar obter ao manter um ativo ou portfólio, geralmente previsto com base em dados históricos de retorno.

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

Onde \(E(R_p)\) é a taxa de retorno esperada do portfólio, \(wi\) é o peso do \(i\)ésimo ativo no portfólio e \(E(R_i)\) é a taxa de retorno esperada do \( i\)ésimo ativo. .

1. Risco (volatilidade ou desvio padrão): Usado para medir a incerteza dos retornos de investimento ou a volatilidade de um investimento.

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

Onde \(\sigma_p\) é o risco total do portfólio e \(\sigma_{ij}\) é a covariância entre o ativo \(i\) e o ativo \(j\), que mede a relação entre as variações de preço dos dois ativos.

1. Covariância: Mede a correlação entre os movimentos de preços de dois ativos.

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

Onde \(\rho_{ij}\) é o coeficiente de correlação entre o ativo \(i\) e o ativo \(j\), \(\sigma_i\) e \(\sigma_j\) são os desvios padrão do ativo \(i\) e do ativo \(j\), respectivamente.

1. Fronteira Eficiente:No sistema de coordenadas risco-retorno, a fronteira eficiente é o conjunto de portfólios que podem fornecer o retorno máximo esperado em um determinado nível de risco.

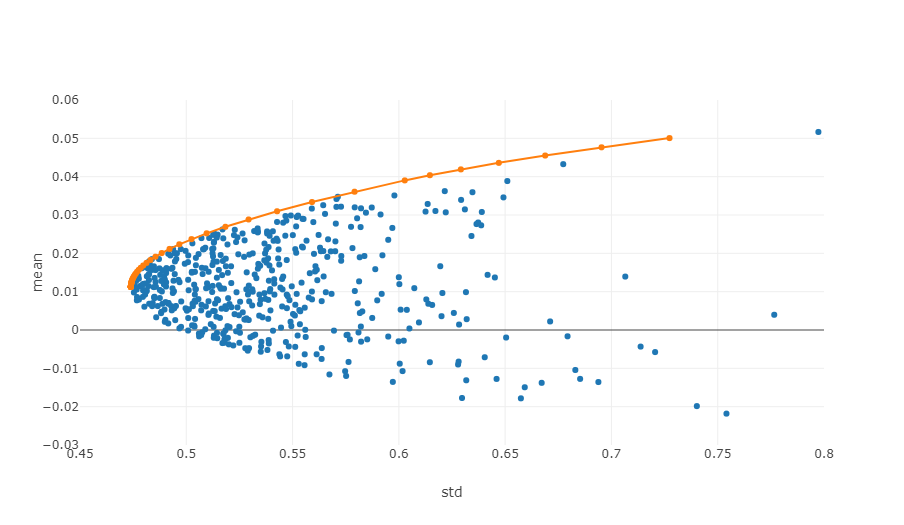
A figura acima é um diagrama esquemático da fronteira efetiva. Cada ponto representa um portfólio de investimentos com pesos diferentes. O eixo horizontal é a volatilidade, ou seja, o nível de risco, e o eixo vertical é a taxa de retorno. Obviamente, focamos na borda superior do gráfico, que alcança o maior retorno no mesmo nível de risco.

Na negociação quantitativa e na gestão de portfólios, a aplicação desses princípios requer análise estatística de dados históricos e o uso de modelos matemáticos para estimar os retornos esperados, desvios-padrão e covariâncias de vários ativos. Em seguida, técnicas de otimização são aplicadas para encontrar a melhor configuração de peso de ativos. Esse processo geralmente envolve cálculos matemáticos complexos e muito processamento computacional, razão pela qual a análise quantitativa se tornou muito importante nas finanças modernas. A seguir, usaremos um exemplo específico do Python para ilustrar como otimizar.

Exemplo de código Python para encontrar a combinação ideal usando o método de simulação

O cálculo do portfólio ótimo de Markowitz é um processo de várias etapas que envolve diversas etapas importantes, como preparação de dados, simulação de portfólio e cálculo de indicadores. Referência: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Obtenha dados de mercado：

   • passarget_dataFunção para obter dados históricos de preços da moeda digital selecionada. Esses são os dados necessários para calcular a taxa de retorno e risco, que são usados ​​para construir carteiras e calcular o índice de Sharpe.

2. Calculando Retorno e Risco：

   • usarcalculate_returns_riskA função calcula a taxa de retorno anualizada e o risco anualizado (desvio padrão) para cada moeda digital. Isso serve para quantificar o desempenho histórico de cada ativo para uso em um portfólio ideal.

3. Calcular o portfólio ótimo de Markowitz：

   • usarcalculate_optimal_portfolioFunção, simulando múltiplos portfólios. Em cada simulação, os pesos dos ativos são gerados aleatoriamente e o retorno e o risco esperados do portfólio são então calculados com base nesses pesos.
   • Ao gerar aleatoriamente combinações de pesos diferentes, vários portfólios possíveis podem ser explorados para encontrar a melhor combinação. Esta é uma das ideias centrais da teoria de portfólio de Markowitz.

O objetivo de todo o processo é encontrar o portfólio que oferece o melhor retorno esperado para um determinado nível de risco. Ao simular múltiplas combinações possíveis, os investidores podem entender melhor o desempenho de diferentes configurações e escolher a combinação que melhor se adapta aos seus objetivos de investimento e tolerância ao risco. Essa abordagem ajuda a otimizar as decisões de investimento e torná-los mais eficientes.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
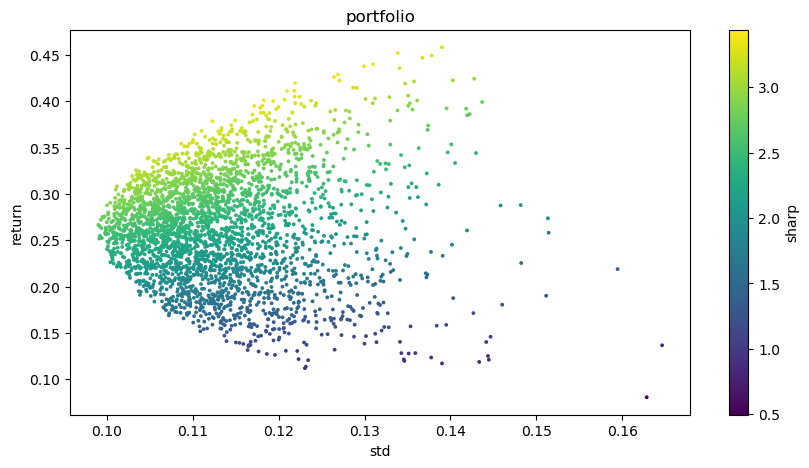
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Resultado final: Melhor combinação: Peso BTCUSDT: 0,0721 Peso ETHUSDT: 0,2704 Peso BNBUSDT: 0,3646 Peso LINKUSDT: 0,1892 Peso BCHUSDT: 0,0829 Peso LTCUSDT: 0,0209 Taxa de retorno esperada: 0,4195 Risco esperado (desvio padrão): 0,1219 Razão de Sharpe: 3,4403