Bayes - O mistério da probabilidade e a inteligência matemática por trás das decisões

A estatística de Bayes é uma forte disciplina universitária em matemática, com amplas aplicações em muitos campos, incluindo finanças, pesquisas médicas e tecnologia da informação. Ela nos permite combinar crenças anteriores com evidências para derivar novas crenças posteriores, permitindo-nos tomar decisões mais inteligentes.

Neste artigo, vamos dar uma breve introdução a alguns dos principais matemáticos que fundaram o campo.

Antes de Bayes Para uma melhor compreensão da estatística bayesiana, precisamos voltar ao século XVIII e referir-nos ao matemático De Moivre e ao seu trabalho O princípio da oportunidade.

Em seu trabalho, De Moivre resolveu muitos problemas relacionados à probabilidade e ao jogo de sua época. Como você pode saber, sua solução para um desses problemas levou à origem da distribuição normal, mas essa é outra história.

A questão mais simples de seu trabalho é:

A bola é jogada três vezes seguidas com uma moeda justa e obtém três probabilidades positivas.

Lendo os problemas descritos no Quadro de Princípios da Aventura, você pode notar que a maioria deles começa com uma hipótese e calcula a probabilidade de um dado evento. Por exemplo, no problema acima, há uma hipótese de que uma moeda é justa e, portanto, a probabilidade de obter um positivo no lançamento é de 0.5.

O que hoje é expresso em termos matemáticos como:

𝑃(𝑋|𝜃)

Mas e se não soubermos se a moeda é justa?𝜃E então?

Thomas Bayes e Richard Price

Quase cinquenta anos mais tarde, em 1763, um trabalho sobre o problema do princípio da solução do cogumelo[2] foi publicado na revista de negociação do cogumelo da Royal Society de Londres.

Nas primeiras páginas do documento, há um texto escrito pelo matemático Richard Price, que resume o conteúdo de um trabalho escrito por seu amigo Thomas Bayes nos anos antes de sua morte. Na introdução, Price explica a importância de algumas descobertas feitas por Thomas Bayes, que não estão envolvidas no teorema de hipótese de De Moivre.

Na verdade, ele se refere a uma questão específica:

A probabilidade de ocorrência de um evento desconhecido é a quantidade de vezes que ele ocorre e falha, e a probabilidade de ocorrência dele é a probabilidade de que ele ocorra entre duas probabilidades nomeadas.

Em outras palavras, depois de observarmos um evento, encontramos um parâmetro desconhecido.θQual é a probabilidade entre dois graus de probabilidade. Este foi, na verdade, um dos primeiros problemas relacionados à inferência estatística na história e deu origem ao nome de probabilidade inversa.

𝑃( 𝜃 | 𝑋）

É claro que esta é a distribuição posterior que hoje chamamos de teorema de Bayes.

Causas não causadas

A partir daí, o grupo começou a trabalhar com os pastores.Thomas BayeseRichard Price (em inglês)O que é o motivo da pesquisa, na verdade, é muito interessante. Mas para fazer isso, precisamos temporariamente deixar de lado algum conhecimento sobre estatística.

Estamos no século XVIII, e a probabilidade está a tornar-se uma área de crescente interesse para os matemáticos. Matemáticos como De Moffat ou Bernoulli já demonstraram que alguns eventos acontecem com um certo grau de aleatoriedade, mas ainda são governados por regras fixas. Por exemplo, se você jogar vários dados, uma sexta parte do tempo ele vai parar em seis.

Agora, imagine que você é um matemático e um religioso devoto que vive nessa época. Você pode estar interessado em saber sobre essa lei oculta e sua relação com Deus.

Esta é, de fato, a questão que Bayes e Price se perguntam. Eles querem resolver a solução para este problema, aplicando-a diretamente para demonstrar que o universo da luz deve ser o resultado da inteligência e da inteligência; portanto, fornecer uma prova da existência de Deus com uma causa final, a luz[2] - isto é, uma causa sem causa.

Raphael

Surpreendentemente, cerca de dois anos mais tarde, em 1774, sem ter lido o artigo de Thomas Bayes, o matemático francês Laplace escreveu um artigo chamado A causa de um evento relacionado com a probabilidade de um evento[3], um artigo sobre o problema da probabilidade inversa.

Os principais princípios:

Se um evento pode ser causado por n causas diferentes, então a proporção entre as probabilidades dessas causas de um dado evento é igual à probabilidade de ocorrência de uma causa dada, e a probabilidade de existência de cada uma dessas causas é igual à probabilidade de ocorrência de uma causa de um dado evento, dividida pela soma das probabilidades de ocorrência de cada uma dessas causas.

O teorema de Bayes é o que conhecemos hoje:

​

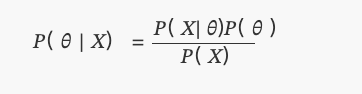
Entre eles:P(θ)A distribuição é uniforme.

Experimento com moedas

Vamos levar a estatística de Bayes até o presente usando o Python e a biblioteca PyMC e fazer um experimento simples.

Suponha que um amigo lhe dê uma moeda e lhe pergunte se você acha que é uma moeda justa. Como ele está com pressa, ele diz que só pode jogar 10 moedas. Como você pode ver, há um parâmetro desconhecido neste problema.pA probabilidade de obter um positivo no lançamento de uma moeda.pO valor mais provável de.

(Nota: não estamos falando de parâmetros)pÉ uma variável aleatória, mas o parâmetro é fixo, e queremos saber entre quais valores é mais provável que ele esteja.

Para ter uma visão diferente sobre o assunto, vamos abordá-lo com duas crenças prévias diferentes:

• 1, você não tem nenhuma informação prévia sobre a equidade das moedas, e você atribui uma probabilidade igual apNesse caso, usaremos o chamado antecedente sem informação, porque você não adicionou nenhuma informação em sua crença.

• 2o, você sabe por experiência que, mesmo que a moeda possa ser injusta, é difícil torná-la muito injusta.pÉ provável que não seja inferior a 0,3 ou superior a 0,7; nesse caso, usaremos um tipo de antecedente de informação.

Para ambas as situações, nossas crenças preliminares seriam as seguintes:

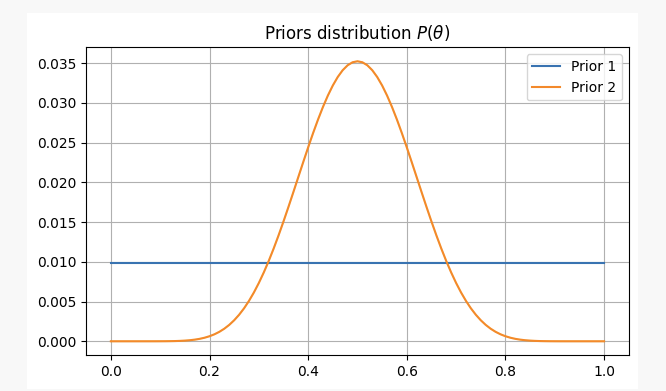
Depois de jogar uma moeda 10 vezes, você tem dois resultados positivos.p？

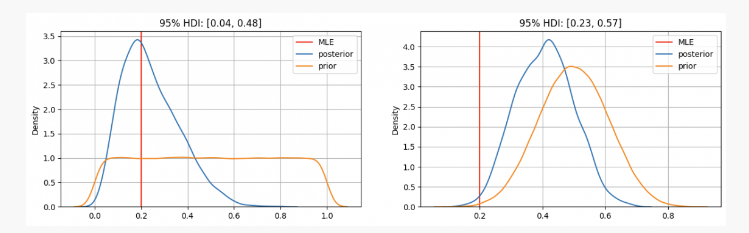
Como você pode ver, no primeiro caso, nós estamos usando um parâmetro.pA distribuição de antecedentes concentra-se na estimativa de maior similaridade (MLE).p=0.2, que é um método semelhante ao método da escola de frequência. Os parâmetros verdadeiramente desconhecidos ficam dentro do intervalo de confiança de 95%, entre 0.04 e 0.48;

Por outro lado, há um alto grau de confiança em que os parâmetrospEm casos que devem estar entre 0.3 e 0.7, podemos ver uma distribuição posterior em torno de 0.4, muito maior do que o valor dado pelo nosso MLE. Neste caso, o verdadeiro parâmetro desconhecido ficará dentro do intervalo de confiança de 95%, entre 0.23 e 0.57.

Assim, no primeiro caso, você diz ao seu amigo que tem certeza de que a moeda não é justa; mas no outro caso, você diz a ele que não tem certeza se a moeda é justa.

Como você pode ver, mesmo com a mesma evidência (dois positivos em cada 10 tentativas), os resultados são diferentes sob diferentes crenças prévias. Esta é uma vantagem da estatística bayesiana, semelhante ao método científico, que nos permite atualizar nossas crenças combinando crenças prévias com novas observações e evidências.

Fim de ano

No artigo de hoje, vemos as origens da estatística bayesiana e seus principais contribuintes. Desde então, muitos outros contribuintes importantes para a área da estatística (Jeffreys, Cox, Shannon, entre outros) têm contribuído para a evolução da estatística.转载自quantdare.com。