Bayes - Desvendando o mistério da probabilidade, explorando a sabedoria matemática por trás da tomada de decisão

A estatística bayesiana é uma disciplina poderosa no campo da matemática, com amplas aplicações em muitas áreas, incluindo finanças, pesquisa médica e tecnologia da informação.

Neste artigo, apresentaremos brevemente alguns dos principais matemáticos que fundaram este campo.

Antes de Bayes Para entender melhor a estatística bayesiana, precisamos voltar ao século XVIII e nos referirmos ao matemático De Moivre e ao seu artigo A Doutrina das Chancelidades.

Em seu artigo, De Moivre resolveu muitos problemas relacionados com probabilidade e jogo em sua época.

Uma das perguntas mais simples no seu artigo foi:

Qual é a probabilidade de obter três cabeças ao lançar uma moeda justa três vezes seguidas?

Ao ler os problemas descritos em A Doutrina das Chancelas, você pode notar que a maioria começa com uma suposição a partir da qual calcula as probabilidades para determinados eventos.

Isto seria expresso hoje em termos matemáticos como:

Fórmula

𝑃(𝑋|𝜃)

No entanto, e se não soubermos se a moeda é justa?𝜃 ?

Thomas Bayes e Richard Price

Quase cinquenta anos depois, em 1763, um artigo intitulado Uma Solução para os Problemas na Doutrina dos Chanceis foi publicado nas Philosophical Transactions da Royal Society de Londres.

Nas primeiras páginas deste documento, há uma peça escrita pelo matemático Richard Price que resume um artigo que seu amigo Thomas Bayes escreveu vários anos antes de sua morte.

Na verdade, ele se referiu a um problema específico:

Dado o número de sucessos e fracassos de um evento desconhecido, encontrar a sua probabilidade entre dois graus.

Em outras palavras, depois de observar um evento, determinamos qual é a probabilidade de um parâmetro desconhecidoθEste é realmente um dos primeiros problemas relacionados com inferência estatística na história e deu origem ao termo inversa probabilidade.

Fórmula

𝑃( 𝜃 | 𝑋）

Isto é, claro, o que chamamos de distribuição posterior do teorema de Bayes hoje.

Pela Razão Sem Causa e Efeito

Compreendendo as motivações por trás da pesquisa destes dois ministros mais velhos,Thomas BayeseRichard PriceMas para fazer isso, precisamos temporariamente deixar de lado algum conhecimento sobre estatística.

Estamos no século XVIII, quando a probabilidade está se tornando um campo cada vez mais interessante para os matemáticos. Matemáticos como de Moivre ou Bernoulli já mostraram que alguns eventos ocorrem com certo grau de aleatoriedade, mas ainda são governados por regras fixas. Por exemplo, se você jogar um dado várias vezes, um sexto das vezes ele vai cair em seis. É como se houvesse uma regra oculta que determina as chances do destino.

Agora imagine-se um matemático e um devoto crente vivendo nesse período. Talvez esteja interessado em entender a relação entre esta regra oculta e Deus.

Esta foi, de fato, a pergunta feita por Bayes e Price. Eles esperavam que sua solução se aplicasse diretamente a provar que o mundo deve ser o resultado de sabedoria e inteligência; portanto, fornecendo evidências da existência de Deus como causa última - isto é, causa sem causalidade.

Laplace

Surpreendentemente, cerca de dois anos depois, em 1774, sem ter lido o artigo de Thomas Bayes, o matemático francês Laplace escreveu um artigo intitulado "Sobre as causas dos eventos pela probabilidade dos eventos", que é sobre problemas de probabilidade inversa.

Se um evento pode ser causado por n razões diferentes, então as proporções entre essas causas probabilidades dadas ao evento são iguais às probabilidades de eventos dadas a essas causas; e a probabilidade de existência de cada causa é igual à probabilidade de causas dadas a este evento dividido pela probabilidade total de eventos dadas a cada uma dessas causas.

Isto é o que conhecemos hoje como o teorema de Bayes:

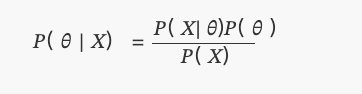
Onde?P(θ)é uma distribuição uniforme.

Experimento com moedas

Vamos trazer estatísticas Bayesianas para o presente usando Python e PyMC biblioteca, e realizar um experimento simples.

Suponha que um amigo lhe dê uma moeda e pergunte se você acha que é uma moeda justa. Porque ele está com pressa, ele lhe diz que você só pode jogar a moeda 10 vezes. Como você pode ver, há um parâmetro desconhecidopNeste problema, que é a probabilidade de obter cabeças no lançamento de moedas, e queremos estimar o valor mais provável dop.

(Nota: Nós não estamos dizendo que o parâmetropé uma variável aleatória, mas sim que este parâmetro é fixo; queremos saber onde é mais provável entre.)

Para ter diferentes pontos de vista sobre este problema, vamos resolvê-lo sob duas crenças prévias diferentes:

• 1. Você não tem nenhuma informação prévia sobre a equidade da moeda, então você atribuir uma probabilidade igual apNesse caso, utilizaremos o que se chama de pré-informação, porque não adicionou nenhuma informação às suas crenças.
• 2. Pela sua experiência, sabe que, mesmo que uma moeda seja injusta, é difícil torná-la extremamente injusta.pÉ improvável que seja inferior a 0,3 ou superior a 0,7.

Para estes dois cenários, as nossas crenças anteriores serão as seguintes:

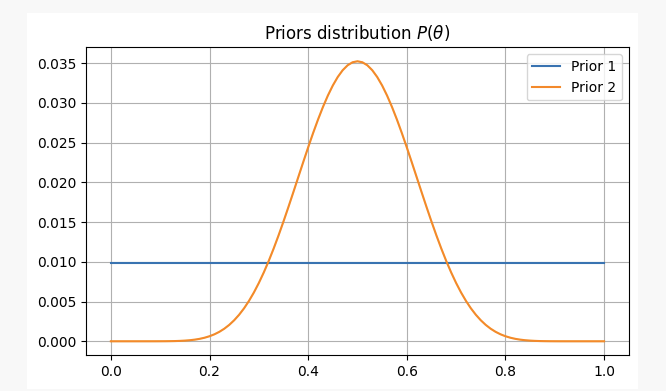
Com esta evidência, onde é provável que encontremos o nosso parâmetrop?

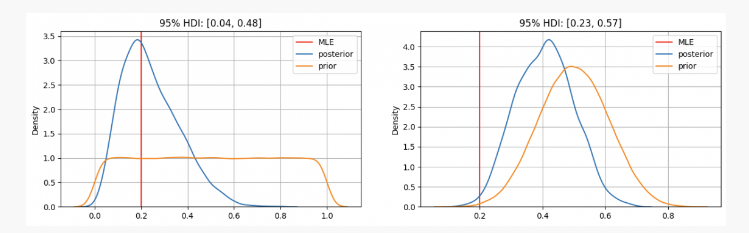
Como você pode ver, no primeiro caso, a nossa distribuição anterior de parâmetropÉ concentrado na estimativa de probabilidade máxima (MLE)p=0.2O verdadeiro parâmetro desconhecido estará dentro do intervalo de confiança de 95%, entre 0,04 e 0,48.

Por outro lado, nos casos em que existe uma elevada confiança, esse parâmetropNeste caso, o verdadeiro parâmetro desconhecido estará dentro de um intervalo de confiança de 95% entre 0,23 e 0,57.

Portanto, no primeiro cenário, você diria ao seu amigo com certeza que esta moeda não é justa, mas em outra situação você diria que não tem certeza se é justa ou não.

Como você pode ver, mesmo quando confrontado com evidências idênticas (duas cabeças de dez lançamentos), sob diferentes crenças anteriores, os resultados podem variar muito; uma vantagem da estatística bayesiana sobre os métodos tradicionais reside aqui: como a metodologia científica, ela nos permite atualizar nossas crenças combinando-as com novas observações e evidências.

Fim de ano

No artigo de hoje, vimos as origens da estatística bayesiana e os seus principais contribuintes.quantdare.com.