Negociação em pares baseada em tecnologia baseada em dados

Negociação em pares baseada em tecnologia baseada em dados

A negociação de pares é um bom exemplo de formulação de estratégias de negociação baseadas em análise matemática. Neste artigo, mostraremos como usar dados para criar e automatizar estratégias de negociação de pares.

Princípios básicos

Suponha que você tenha um par de alvos de investimento X e Y que tenham algumas conexões potenciais. Por exemplo, duas empresas produzem os mesmos produtos, como a Pepsi Cola e a Coca Cola. Você quer que a relação de preço ou os spreads de base (também conhecidos como diferença de preço) dos dois permaneçam inalterados ao longo do tempo. No entanto, devido às mudanças temporárias na oferta e demanda, como uma grande ordem de compra / venda de um alvo de investimento e a reação às notícias importantes de uma das empresas, a diferença de preço entre os dois pares pode ser diferente de tempos em tempos. Neste caso, um objeto de investimento sobe enquanto o outro desce em relação ao outro. Se você quiser que esse desacordo volte ao normal ao longo do tempo, você pode encontrar oportunidades de negociação (ou oportunidades de arbitragem).

Quando há uma diferença temporária de preço, você venderá o objeto de investimento com excelente desempenho (o objeto de investimento em alta) e comprará o objeto de investimento com baixo desempenho (o objeto de investimento em queda). Você tem certeza de que a margem de juros entre os dois objetos de investimento acabará caindo através da queda do objeto de investimento com excelente desempenho ou a ascensão do objeto de investimento com baixo desempenho, ou ambos. Sua transação fará dinheiro em todas essas situações semelhantes. Se os objetos de investimento subirem ou descerem juntos sem mudar a diferença de preço entre eles, você não fará ou perderá dinheiro.

Por conseguinte, a negociação de pares é uma estratégia de negociação neutra do mercado, que permite aos operadores beneficiarem de quase todas as condições de mercado: tendência ascendente, tendência descendente ou consolidação horizontal.

Explique o conceito: dois objetivos de investimento hipotéticos

• Construir o nosso ambiente de investigação na plataforma FMZ Quant

Em primeiro lugar, para trabalhar sem problemas, precisamos de construir o nosso ambiente de investigação.FMZ.COM) para construir o nosso ambiente de investigação, principalmente para utilizar a interface API conveniente e rápida e o sistema Docker bem empacotado desta plataforma mais tarde.

No nome oficial da plataforma FMZ Quant, este sistema Docker é chamado de sistema Docker.

Por favor, consulte meu artigo anterior sobre como implantar um docker e robô:https://www.fmz.com/bbs-topic/9864.

Os leitores que desejam comprar seu próprio servidor de computação em nuvem para implantar dockers podem consultar este artigo:https://www.fmz.com/digest-topic/5711.

Depois de implantar o servidor de computação em nuvem e o sistema docker com sucesso, em seguida, vamos instalar o maior artefato atual do Python: Anaconda

Para realizar todos os ambientes de programa relevantes (bibliotecas de dependências, gerenciamento de versões, etc.) necessários neste artigo, a maneira mais simples é usar o Anaconda.

Para o método de instalação do Anaconda, consulte o guia oficial do Anaconda:https://www.anaconda.com/distribution/.

Este artigo também usará numpy e pandas, duas bibliotecas populares e importantes na computação científica Python.

O trabalho básico acima também pode se referir aos meus artigos anteriores, que introduzem como configurar o ambiente Anaconda e as bibliotecas numpy e pandas.https://www.fmz.com/bbs-topic/9863.

Em seguida, vamos usar código para implementar um dois objetivos de investimento hipotéticos:

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Sim, também vamos usar matplotlib, uma biblioteca de gráficos muito famosa em Python.

Vamos gerar uma meta de investimento hipotética X, e simular e traçar seu retorno diário através da distribuição normal.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

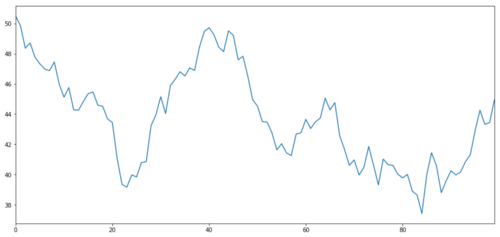
O X do objecto de investimento é simulado para traçar o seu rendimento diário através de uma distribuição normal

Agora nós geramos Y, que é fortemente integrado com X, então o preço de Y deve ser muito semelhante à mudança de X. Nós modela-lo tomando X, movendo-o para cima e adicionando algum ruído aleatório extraído da distribuição normal.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

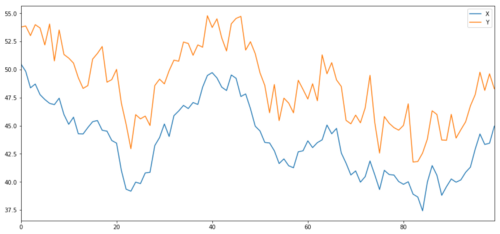
X e Y do objecto de investimento de cointegração

Cointegração

A cointegração é muito semelhante à correlação, o que significa que a relação entre duas séries de dados mudará perto do valor médio.

Y = X + e

Onde é uma proporção constante e e é o ruído.

Para os pares de negociação entre duas séries temporais, o valor esperado da relação ao longo do tempo deve convergir para o valor médio, ou seja, eles devem ser cointegrados. A série temporal que construímos acima é cointegrada. Vamos traçar a relação entre eles agora para que possamos ver como ela se parece.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

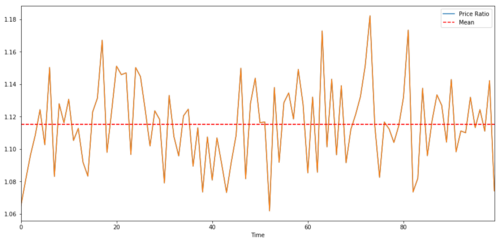
Relação e valor médio entre dois preços-alvo de investimento cointegrados

Teste de cointegração

Um método de teste conveniente é usar statsmodels.tsa.stattools. Veremos um valor de p muito baixo, porque criamos duas séries de dados artificialmente que são tão co-integradas quanto possível.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

O resultado é: 1.81864477307e-17

Nota: correlação e cointegração

Correlação e cointegração, embora semelhantes em teoria, não são a mesma coisa. Vamos olhar para exemplos de séries de dados relevantes, mas não cointegradas e vice-versa.

X.corr(Y)

O resultado é: 0,951

Como esperávamos, isso é muito alto. mas o que dizer de duas séries relacionadas, mas não co-integradas? um exemplo simples é uma série de dois dados desviantes.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

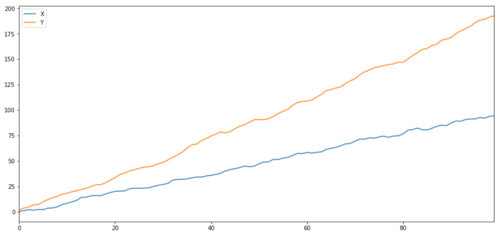
Duas séries relacionadas (não integradas)

Coeficiente de correlação: 0,998 Valor P do ensaio de cointegração: 0,258

Exemplos simples de cointegração sem correlação são sequências de distribuição normal e ondas quadradas.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

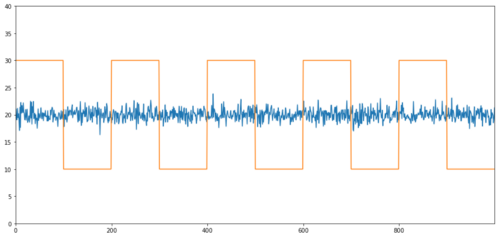
Correlação: 0,007546 Valor P do ensaio de cointegração: 0,0

A correlação é muito baixa, mas o valor p mostra uma co-integração perfeita!

Como conduzir a negociação de pares?

Como duas séries temporais co-integradas (como X e Y acima) estão de frente e se desviando uma da outra, às vezes os spreads de base são altos ou baixos. Nós conduzimos negociação de pares comprando um objeto de investimento e vendendo outro. Desta forma, se as duas metas de investimento caírem ou subirem juntas, não ganharemos nem perderemos dinheiro, ou seja, somos neutros no mercado.

De volta ao acima, X e Y em Y = X + e, de modo que a relação (Y / X) se move em torno de seu valor médio . Ganhamos dinheiro através da relação de reversão do valor médio. Para fazer isso, vamos prestar atenção no caso em que X e Y estão muito distantes, ou seja, o valor de é muito alto ou muito baixo:

• Quando a relação é muito pequena e esperamos que ela aumente. no exemplo acima, abrimos a posição indo longo Y e indo curto X.

• A proporção de curto prazo é quando a proporção é muito grande e esperamos que ela diminua.

Por favor, note que temos sempre uma posição de cobertura: se o sujeito da negociação compra valor de perda, a posição curta irá fazer dinheiro, e vice-versa, por isso somos imunes à tendência geral do mercado.

Se o X e o Y do objeto de negociação se moverem em relação um ao outro, ganharemos dinheiro ou perderemos dinheiro.

Usar dados para encontrar objetos de negociação com comportamento semelhante

A melhor forma de fazer isso é começar com o assunto de negociação que você suspeita que pode ser a cointegração e realizar um teste estatístico.Viés de comparação múltipla.

Viés de comparação múltiplase refere ao aumento da chance de gerar incorretamente valores p importantes ao executar muitos testes, porque precisamos executar um grande número de testes. Se executarmos 100 testes em dados aleatórios, devemos ver 5 valores p abaixo de 0,05. Se você quiser comparar n alvos de negociação para cointegração, você realizará n (n-1) / 2 comparações, e você verá muitos valores p incorretos, que aumentarão com o aumento de suas amostras de teste. Para evitar essa situação, selecione alguns pares de negociação e você tem razão para determinar que eles podem ser cointegração, e depois teste-os separadamente. Isso reduzirá muitoViés de comparação múltipla.

Portanto, vamos tentar encontrar alguns alvos de negociação que mostram co-integração. Vamos tomar uma cesta de grandes ações de tecnologia dos EUA no Índice S&P 500 como exemplo. Estes alvos de negociação operam em segmentos de mercado semelhantes e têm preços de co-integração.

A matriz de pontuação do teste de cointegração devolvida, a matriz de valor p e todos os pares com valor p inferior a 0,05.Este método é propenso ao viés de comparação múltipla, por isso, na verdade, eles precisam realizar uma segunda verificação.Neste artigo, por conveniência de nossa explicação, escolhemos ignorar este ponto no exemplo.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Nota: Incluímos o benchmark de mercado (SPX) nos dados - o mercado tem impulsionado o fluxo de muitos objetos de negociação. Normalmente, você pode encontrar dois objetos de negociação que parecem estar cointegrados; Mas, na verdade, eles não cointegram uns com os outros, mas com o mercado. Isso é chamado de variável de confusão. É importante verificar a participação do mercado em qualquer relação que você encontrar.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Agora vamos tentar usar nosso método para encontrar pares de negociação cointegrados.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

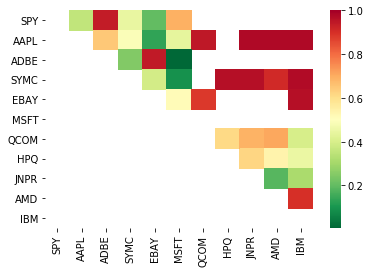
Parece que ADBE e MSFT estão cointegrados.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

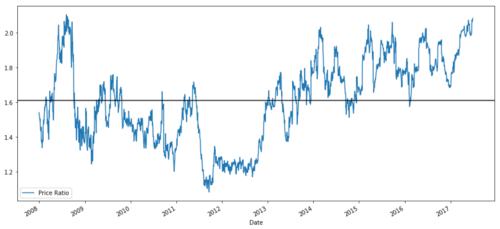
Grafico do rácio de preços entre MSFT e ADBE de 2008 a 2017

Esta proporção parece uma média estável. As proporções absolutas não são estatisticamente úteis. É mais útil padronizar nossos sinais tratando-os como pontuação Z. A pontuação Z é definida como:

Ponto Z (valor) = (valor média) / Desvio-padrão

Alerta

Na verdade, geralmente tentamos expandir os dados com a premissa de que os dados são normalmente distribuídos. No entanto, muitos dados financeiros não são normalmente distribuídos, por isso devemos ter muito cuidado para não simplesmente assumir normalidade ou qualquer distribuição específica ao gerar estatísticas. A verdadeira distribuição de rácios pode ter um efeito de rabo de gordura, e esses dados que tendem a ser extremos confundirão nosso modelo e levarão a grandes perdas.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

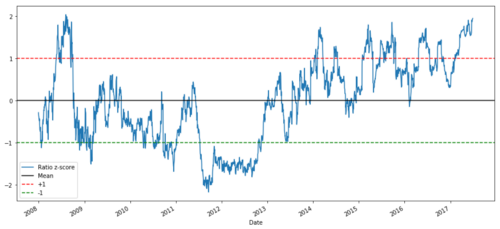
Relação de preços Z entre MSFT e ADBE de 2008 a 2017

Agora é mais fácil observar o movimento do rácio perto do valor médio, mas às vezes é fácil ter uma grande diferença do valor médio.

Agora que discutimos os conhecimentos básicos da estratégia de negociação de pares e determinamos o assunto da integração conjunta com base no preço histórico, vamos tentar desenvolver um sinal de negociação.

• Recolher dados fiáveis e limpar os dados;

• Criar funções a partir de dados para identificar sinais/lógica de negociação;

• As funções podem ser médias móveis ou dados de preços, correlações ou proporções de sinais mais complexos - combiná-los para criar novas funções;

• Use estas funções para gerar sinais de negociação, ou seja, quais sinais estão comprando, vendendo ou posições curtas para observar.

Felizmente, temos a plataforma FMZ Quant (fmz.comA Comissão propõe a criação de uma base de dados para a análise dos resultados da investigação e do desenvolvimento.

Na plataforma FMZ Quant, existem interfaces encapsuladas para várias trocas convencionais. O que precisamos fazer é chamar essas interfaces de API. O resto da lógica de implementação subjacente foi concluído por uma equipe profissional.

Para completar a lógica e explicar o princípio neste artigo, apresentaremos essas lógicas subjacentes em detalhes.

Vamos começar:

Passo 1: Prepare sua pergunta

Aqui, nós tentamos criar um sinal para nos dizer se a relação vai comprar ou vender no próximo momento, ou seja, a nossa variável de previsão Y:

Y = Relação é compra (1) ou venda (-1)

Y(t)= Sign(Ratio(t+1) Ratio(t))

Por favor, note que não precisamos prever o preço-alvo real da transação, ou mesmo o valor real do rácio (embora possamos), mas apenas a direção do rácio na próxima etapa.

Passo 2: recolha de dados fiáveis e precisos

FMZ Quant é seu amigo! Você só precisa especificar o objeto de transação a ser negociado e a fonte de dados a ser usada, e ele irá extrair os dados necessários e limpá-lo para dividendos e divisão de objeto de transação.

Para os dias de negociação dos últimos 10 anos (cerca de 2500 pontos de dados), obtivemos os seguintes dados utilizando o Yahoo Finance: preço de abertura, preço de fechamento, preço mais alto, preço mais baixo e volume de negociação.

Passo 3: Dividir os dados

Não se esqueça desta etapa muito importante para testar a precisão do modelo: estamos a utilizar os seguintes dados para a divisão de formação/validação/teste.

• Formação 7 anos ~ 70%

• Teste ~ 3 anos 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

Idealmente, deveríamos também fazer conjuntos de validação, mas não o faremos por enquanto.

Etapa 4: Engenharia de características

Qual pode ser a função relacionada? Queremos prever a direção da mudança da taxa. Vimos que nossos dois alvos de negociação são cointegrados, então essa taxa tende a mudar e retornar ao valor médio. Parece que nossas características devem ser algumas medidas da taxa média, e a diferença entre o valor atual e o valor médio pode gerar nosso sinal de negociação.

Usamos as seguintes funções:

• Relação da média móvel de 60 dias: medição da média móvel;

• Relatório da média móvel de 5 dias: medição do valor atual da média;

• Desvio-padrão de 60 dias;

• Pontuação Z: (5d MA - 60d MA) / 60d SD.

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

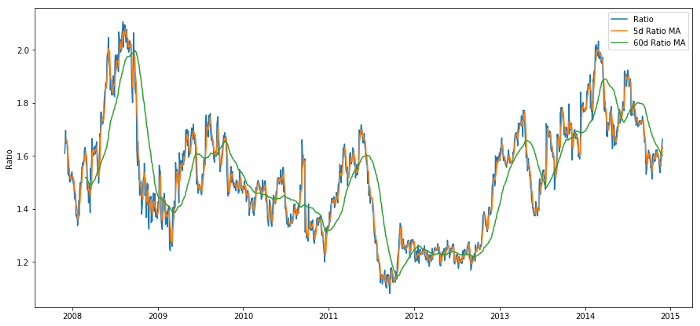
Relação de preços entre 60d e 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

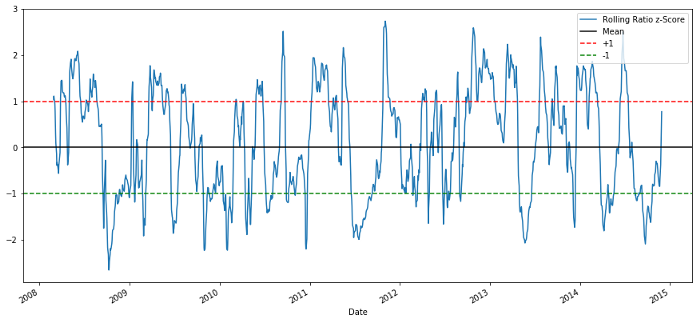
60-5 Z Relações de preços

A pontuação Z do valor da média móvel traz a propriedade de regressão do valor médio da razão!

Etapa 5: Selecção do modelo

Vamos começar com um modelo muito simples. Olhando para o gráfico de pontuação z, podemos ver que se a pontuação z for muito alta ou muito baixa, ela retornará.

• Quando z é inferior a - 1,0, a razão é comprar (1), porque esperamos que z retorne a 0, então a razão aumenta;

• Quando z é superior a 1,0, a razão é vender (- 1), porque esperamos que z retorne a 0, então a razão diminui.

Etapa 6: Formação, verificação e otimização

Por fim, vamos dar uma olhada no impacto real do nosso modelo sobre os dados reais.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

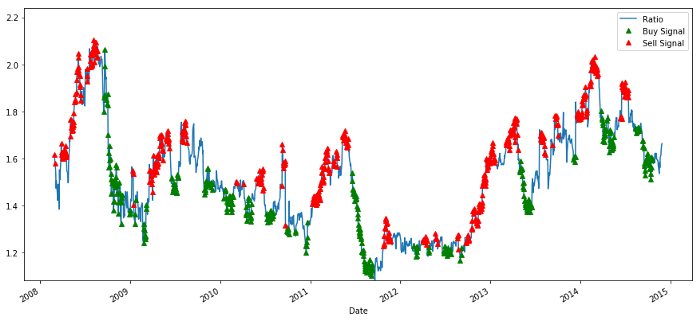
Indicação do rácio de preços de compra e venda

O sinal parece razoável. Nós parecemos vender quando ele é alto ou aumentando (pontos vermelhos) e comprá-lo de volta quando ele é baixo (pontos verdes) e diminuindo.

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

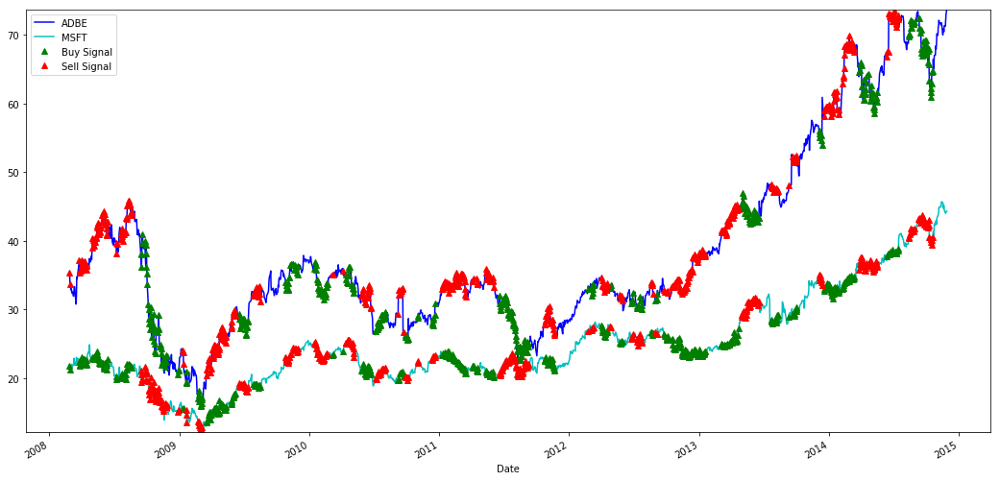
Sinais de compra e venda de ações do MSFT e do ADBE

Por favor, preste atenção em como às vezes fazemos lucros com pernas curtas, às vezes com pernas longas, e às vezes com ambas.

Nós estamos satisfeitos com o sinal dos dados de treinamento. Vamos ver que tipo de lucro esse sinal pode gerar. Quando a proporção é baixa, podemos fazer um teste de retorno simples, comprar uma proporção (compre 1 ação ADBE e venda proporção x ação MSFT), e vender uma proporção (vender 1 ação ADBE e comprar x ação MSFT) quando ela é alta, e calcular as transações PnL dessas proporções.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

O resultado é: 1783.375

Agora, podemos otimizar ainda mais alterando a janela de tempo média móvel, alterando os limiares de compra / venda e posições fechadas, e verificar a melhoria do desempenho dos dados de validação.

Também podemos tentar modelos mais complexos, como a regressão logística e SVM, para prever 1/-1.

Agora, vamos avançar neste modelo, o que nos leva a:

Etapa 7: Reexame dos dados do ensaio

Aqui, novamente, a plataforma FMZ Quant adota um mecanismo de backtesting QPS / TPS de alto desempenho para reproduzir o ambiente histórico verdadeiramente, eliminar armadilhas comuns de backtesting quantitativo e descobrir as deficiências das estratégias em tempo útil, de modo a ajudar melhor o investimento real do bot.

Para explicar o princípio, este artigo ainda escolhe mostrar a lógica subjacente. Na aplicação prática, recomendamos aos leitores que usem a plataforma FMZ Quant. Além de economizar tempo, é importante melhorar a taxa de tolerância a falhas.

O backtesting é simples. Podemos usar a função acima para ver o PnL dos dados do teste.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

O resultado é: 5262.868

Tornou-se o nosso primeiro modelo simples de troca de pares.

Evitar o sobreajuste

Antes de concluir a discussão, eu gostaria de discutir sobre o sobreajuste em particular. O sobreajuste é a armadilha mais perigosa nas estratégias de negociação. O algoritmo de sobreajuste pode ter um desempenho muito bom no backtest, mas falha nos novos dados invisíveis - o que significa que ele não revela realmente nenhuma tendência dos dados e não tem capacidade de previsão real.

Em nosso modelo, usamos parâmetros de rolagem para estimar e otimizar o comprimento da janela de tempo. Podemos decidir simplesmente iterar sobre todas as possibilidades, um comprimento razoável de janela de tempo e escolher o comprimento de tempo de acordo com o melhor desempenho do nosso modelo. Vamos escrever um loop simples para marcar o comprimento da janela de tempo de acordo com o pnl dos dados de treinamento e encontrar o melhor loop.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Agora examinamos o desempenho do modelo nos dados do teste, e descobrimos que este tempo de janela de comprimento está longe de ser ideal!

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

É óbvio que os dados de amostragem adequados para nós nem sempre produzirão bons resultados no futuro.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

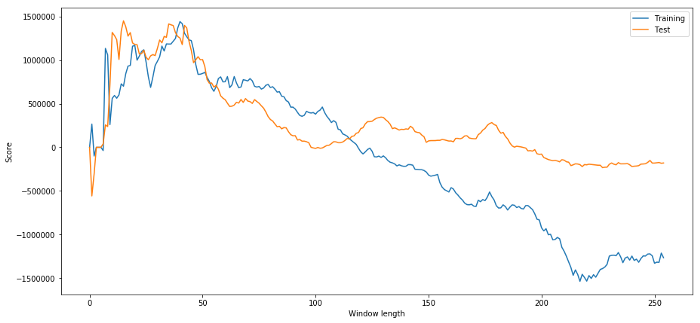
Podemos ver que qualquer coisa entre 20 e 50 é uma boa escolha para janelas de tempo.

Para evitar o sobreajuste, podemos usar o raciocínio econômico ou a natureza do algoritmo para selecionar o comprimento da janela de tempo.

Próximo passo

Neste artigo, propomos alguns métodos de introdução simples para demonstrar o processo de desenvolvimento de estratégias de negociação.

• Exponente de Hurst;

• Tempo de meia-vida da regressão média inferida do processo de Ornstein-Uhlenbeck;

• Filtro Kalman.

Relacionados

Mais.