Realização de estratégias equitativas equilibradas de posições longas-cortas com um alinhamento ordenado

Realização de estratégias equitativas equilibradas de posições longas-cortas com um alinhamento ordenado

No artigo anterior (https://www.fmz.com/bbs-topic/9862), introduzimos estratégias de negociação de pares e demonstrámos como criar e automatizar estratégias de negociação utilizando dados e análise matemática.

A estratégia de equidade equilibrada de posições longas e curtas é uma extensão natural da estratégia de negociação de pares aplicável a uma cesta de objetos de negociação. É particularmente adequada para mercados de negociação com muitas variedades e inter-relações, como mercados de moeda digital e mercados de futuros de commodities.

Princípios básicos

A estratégia de equidade equilibrada de posições longas e curtas é longo e curto uma cesta de alvos de negociação simultaneamente. Assim como a negociação de pares, determina qual alvo de investimento é barato e qual alvo de investimento é caro. A diferença é que a estratégia de equidade equilibrada de posições longas e curtas irá organizar todos os alvos de investimento em um pool de seleção de ações para determinar quais alvos de investimento são relativamente baratos ou caros.

Você se lembra do que dissemos que a negociação de pares é uma estratégia neutra de mercado? O mesmo vale para a estratégia equitativa equilibrada de posições curtas longas, porque a quantidade igual de posições longas e curtas garante que a estratégia permanecerá neutra de mercado (não afetada por flutuações do mercado). A estratégia também é estatisticamente robusta; Ao classificar os objetivos de investimento e manter posições longas, você pode abrir posições em seu modelo de classificação muitas vezes, não apenas uma vez.

Qual é o esquema de classificação?

O esquema de classificação é um modelo que pode atribuir prioridade a cada assunto de investimento de acordo com o desempenho esperado. Os fatores podem ser fatores de valor, indicadores técnicos, modelos de preços ou uma combinação de todos os fatores acima. Por exemplo, você pode usar indicadores de impulso para classificar uma série de alvos de investimento de rastreamento de tendências: espera-se que os alvos de investimento com o maior impulso continuem a ter um bom desempenho e obtenham a maior classificação; O objeto de investimento com o menor impulso tem o pior desempenho e os menores retornos.

O sucesso desta estratégia depende quase inteiramente do esquema de classificação utilizado, ou seja, o seu esquema de classificação pode separar o alvo de investimento de alto desempenho do alvo de investimento de baixo desempenho, de modo a realizar melhor o retorno da estratégia de metas de investimento de posições longas e curtas.

Como fazer um esquema de classificação?

Uma vez que tenhamos determinado o esquema de classificação, esperamos obter lucro com ele. Fazemos isso investindo a mesma quantidade de capital para longar as metas de investimento mais altas e curto as metas de investimento mais baixas. Isso garante que a estratégia só faça lucros proporcionais à qualidade do ranking, e será neutral de mercado.

Suponha que você está classificando todos os objetivos de investimento m, e você tem n dólares para investimento, e você quer manter um total de 2p (onde m> 2p) posições.

• Você classifica os objetos de investimento como: 1,...,p posição, ir curto a meta de investimento de 2/2p USD.

• Você classifica os objetos de investimento como: m-p,...,m posição, vá longo a meta de investimento de n/2p USD.

Nota: Como o preço do objeto de investimento causado pela flutuação de preços nem sempre dividirá n/2p uniformemente, e alguns objetos de investimento devem ser comprados com números inteiros, haverá alguns algoritmos imprecisos, que devem estar o mais perto possível desse número.

n/2p = 100000/1000 = 100

Isso causará um grande problema para pontuações com um preço superior a 100 (como o mercado de futuros de commodities), porque você não pode abrir uma posição com um preço fracionário (este problema não existe nos mercados de moeda digital).

Tomemos um exemplo hipotético.

• Construir o nosso ambiente de investigação na plataforma FMZ Quant

Em primeiro lugar, para trabalhar sem problemas, precisamos de construir o nosso ambiente de investigação.FMZ.COM) para construir o nosso ambiente de investigação, principalmente para utilizar a interface API conveniente e rápida e o sistema Docker bem empacotado desta plataforma mais tarde.

No nome oficial da plataforma FMZ Quant, este sistema Docker é chamado de sistema Docker.

Por favor, consulte meu artigo anterior sobre como implantar um docker e robô:https://www.fmz.com/bbs-topic/9864.

Os leitores que desejam comprar seu próprio servidor de computação em nuvem para implantar dockers podem consultar este artigo:https://www.fmz.com/digest-topic/5711.

Depois de implantar o servidor de computação em nuvem e o sistema docker com sucesso, em seguida, vamos instalar o maior artefato atual do Python: Anaconda

Para realizar todos os ambientes de programa relevantes (bibliotecas de dependências, gerenciamento de versões, etc.) necessários neste artigo, a maneira mais simples é usar o Anaconda.

Para o método de instalação do Anaconda, consulte o guia oficial do Anaconda:https://www.anaconda.com/distribution/.

Este artigo também usará numpy e pandas, duas bibliotecas populares e importantes na computação científica Python.

O trabalho básico acima também pode se referir aos meus artigos anteriores, que introduzem como configurar o ambiente Anaconda e as bibliotecas numpy e pandas.https://www.fmz.com/digest-topic/9863.

Nós geramos alvos de investimento aleatórios e fatores aleatórios para classificá-los.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

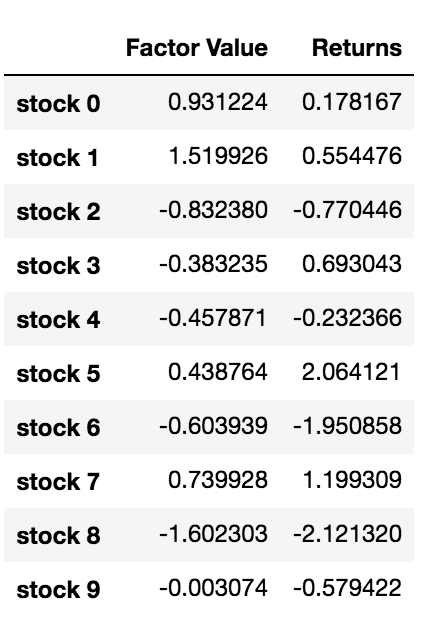
Agora que temos os valores dos fatores e retornos, podemos ver o que acontece se classificarmos os objetivos de investimento com base nos valores dos fatores e, em seguida, abrir posições longas e curtas.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

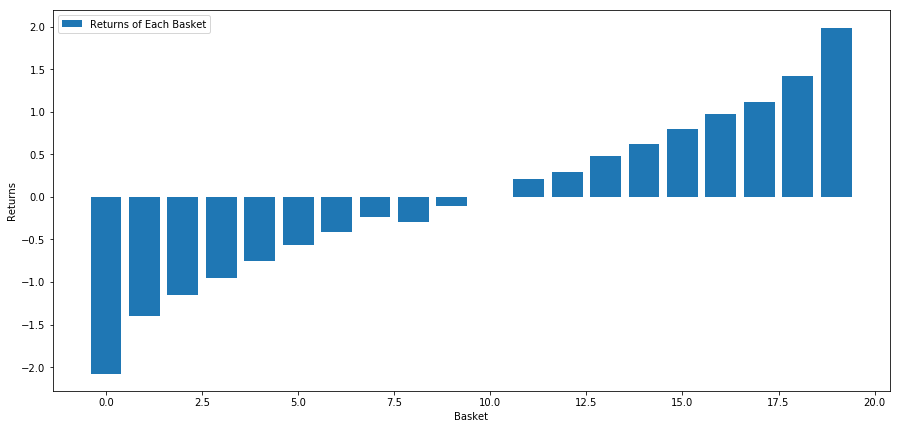
A nossa estratégia é a de longar a primeira cesta classificada de pools de investimento alvo; ir curto da décima cesta classificada.

basket_returns[number_of_baskets-1] - basket_returns[0]

O resultado é: 4.172

Põe dinheiro no nosso modelo de classificação para que possa separar metas de investimento de alto desempenho de metas de investimento de baixo desempenho.

No restante deste artigo, discutiremos como avaliar o esquema de classificação. A vantagem da arbitragem baseada em classificação é que ela não é afetada pela desordem do mercado, em vez disso, a desordem do mercado pode ser usada.

Consideremos um exemplo do mundo real.

Carregámos dados de 32 acções de diferentes indústrias no índice S&P 500 e tentámos classificá-las.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Utilizemos o indicador de ímpeto padronizado para um período de um mês como base para a classificação.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()['Adj Close']
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Agora vamos analisar o comportamento de nossas ações e ver como nossas ações operam no mercado no fator de classificação que escolhemos.

Analise os dados

Comportamento das existências

Vamos ver como nossa cesta selecionada de ações se comporta em nosso modelo de classificação. Para fazer isso, vamos calcular o retorno forward semanal para todas as ações. Então podemos ver a correlação entre o retorno forward de 1 semana de cada ação e o impulso dos 30 dias anteriores. As ações que mostram correlação positiva são seguidores de tendência, enquanto as ações que mostram correlação negativa são inversões médias.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = ['Scores', 'pvalues'])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values('Scores', inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations['Scores'])
plt.xlabel('Stocks')
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend(['Correlation over All Data'])
plt.ylabel('Correlation between %s day Momentum Scores and %s-day forward returns by Stock'%(day,forward_return_day));
plt.show()

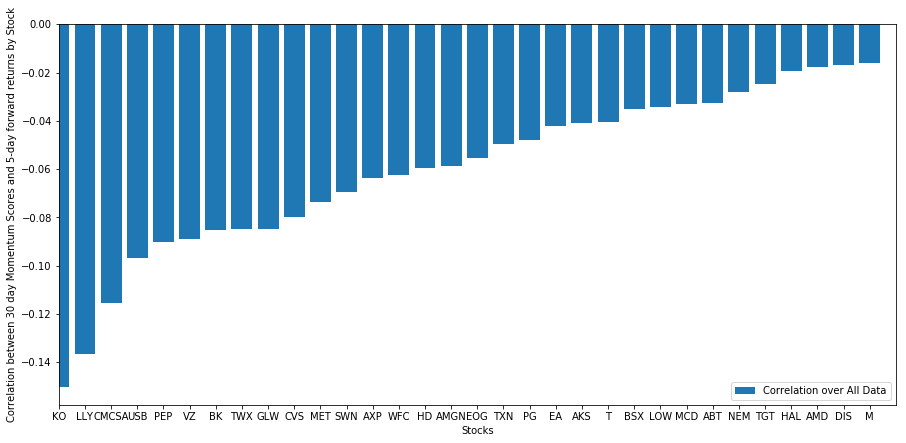
Todas as nossas ações têm uma reversão média até certo ponto! (Obviamente, o universo que escolhemos funciona assim.) Isso nos diz que se as ações se classificam em primeiro lugar na análise de impulso, devemos esperar que elas se apresentem mal na próxima semana.

Correlação entre a classificação dos resultados da análise do ímpeto e os retornos

Em seguida, precisamos ver a correlação entre nossas pontuações de classificação e os retornos futuros globais do mercado, ou seja, a relação entre a taxa de retorno prevista e nosso fator de classificação.

Para este fim, calculamos a correlação diária entre o impulso de 30 dias de todas as ações e o retorno a prazo de 1 semana.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = ['Scores', 'pvalues'])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores['pvalues'].loc[i] = pvalue
    correl_scores['Scores'].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores['Scores'])
plt.hlines(np.mean(correl_scores['Scores']), 1,l+1, colors='r', linestyles='dashed')
plt.xlabel('Day')
plt.xlim((1, l+1))
plt.legend(['Mean Correlation over All Data', 'Daily Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

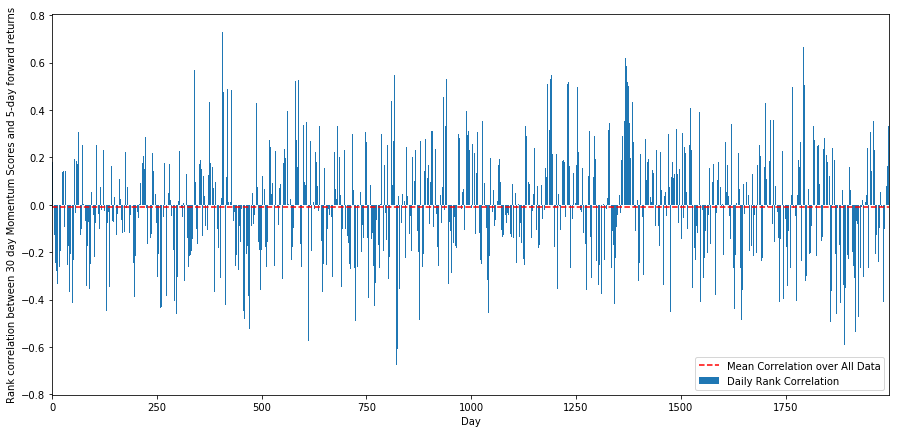
As correlações diárias mostram uma correlação muito complexa mas muito leve (o que é esperado uma vez que dissemos que todas as ações retornarão à média).

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

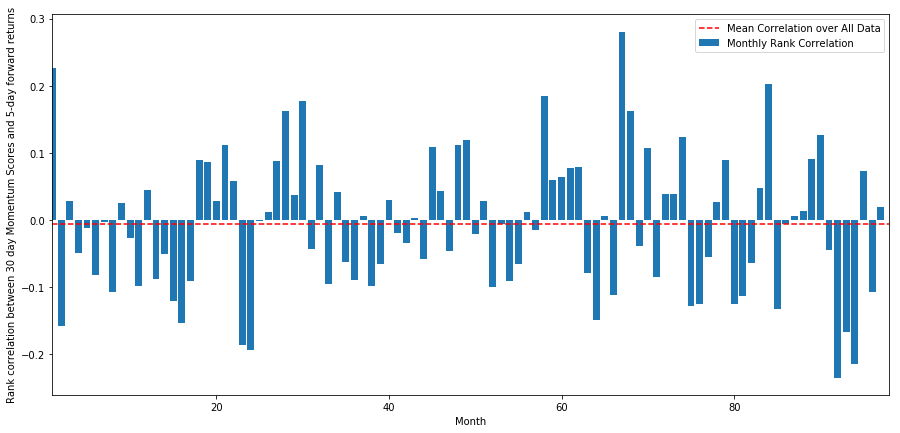
Podemos ver que a correlação média é novamente ligeiramente negativa, mas também muda muito a cada mês.

Retorno médio de um cesto de ações

Calculamos o retorno de uma cesta de ações tomadas do nosso ranking. Se classificamos todas as ações e as dividimos em nn grupos, qual é o retorno médio de cada grupo?

O primeiro passo é criar uma função que dê o retorno médio e o fator de classificação de cada cesta dada a cada mês.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Quando classificamos as ações com base nesta pontuação, calculamos o rendimento médio de cada cesta.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

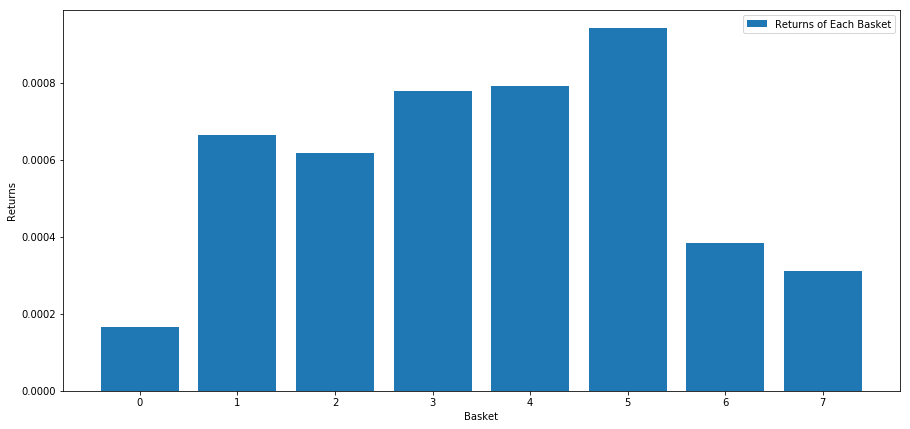
Parece que podemos separar os que têm um bom desempenho dos que têm um mau.

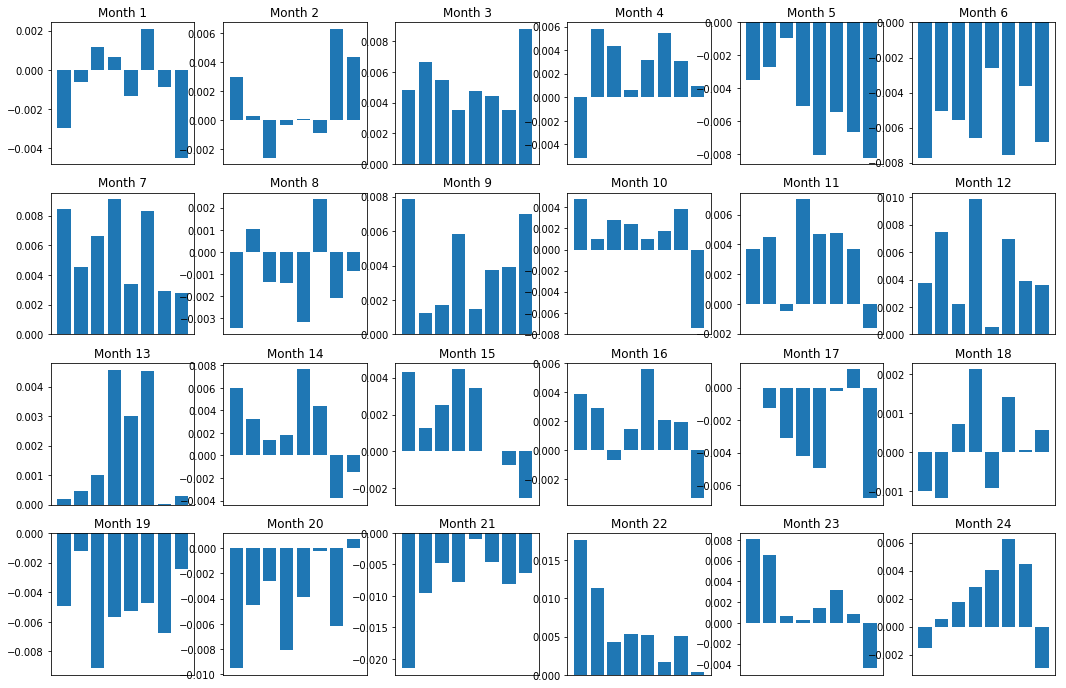
Consistência da margem (base)

Naturalmente, estas são apenas relações médias. A fim de entender como a relação é consistente e se estamos dispostos a negociar, devemos mudar nossa abordagem e atitude para ele ao longo do tempo. Em seguida, vamos olhar para a sua margem de juros mensal (base) para os dois anos anteriores.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel('Returns')
plt.xlabel('Month')
plt.plot(strategy_returns.cumsum())
plt.legend(['Monthly Strategy Returns', 'Cumulative Strategy Returns'])
plt.show()

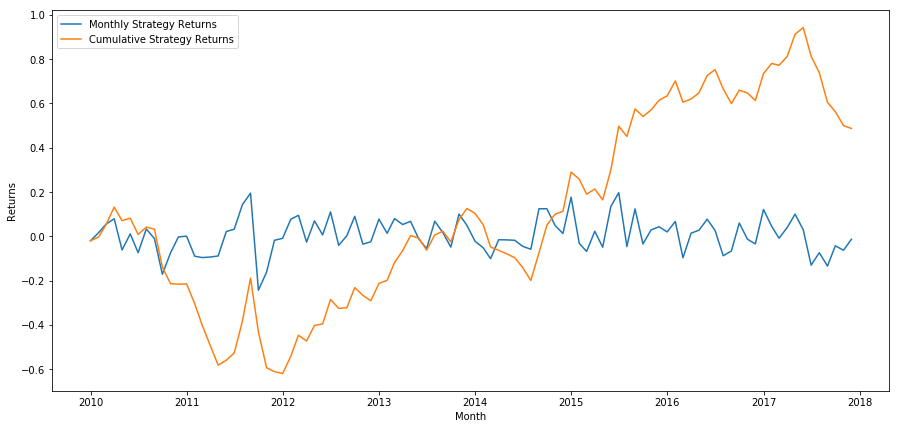
Por fim, se nós vamos long a última cesta e vamos curto a primeira cesta a cada mês, então vamos olhar para os retornos (assumindo igual alocação de capital por título).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Taxas anuais de rendimento: 5,03%

O que podemos ver é que temos um esquema de classificação muito fraco, que só pode distinguir delicadamente as acções de alto desempenho das acções de baixo desempenho.

Encontrar o esquema de classificação correto

Para realizar a estratégia de equidade equilibrada de longo prazo, na verdade, você só precisa determinar o esquema de classificação. Tudo depois disso é mecânico. Uma vez que você tem uma estratégia de equidade equilibrada de longo prazo, você pode trocar diferentes fatores de classificação sem muita mudança. É uma maneira muito conveniente de iterar suas ideias rapidamente sem se preocupar em ajustar todo o código a cada vez.

O esquema de classificação também pode vir de quase qualquer modelo. Não é necessariamente um modelo de fator baseado em valor. Pode ser uma tecnologia de aprendizado de máquina que pode prever retornos um mês de antecedência e classificar de acordo com esse nível.

Selecção e avaliação do sistema de classificação

O esquema de classificação é a vantagem e a parte mais importante da estratégia equitativa equilibrada de curto e longo prazos.

Um bom ponto de partida é selecionar tecnologias conhecidas existentes e ver se você pode modificá-las ligeiramente para obter retornos mais elevados.

• Clone e ajuste: Escolha um tópico que é frequentemente discutido e veja se você pode modificá-lo ligeiramente para ganhar vantagens. Geralmente, os fatores disponíveis publicamente não terão mais sinais de negociação, porque eles se arbitraram completamente do mercado. Mas às vezes eles o levarão na direção certa.

• Modelo de preços: Qualquer modelo que prevê retornos futuros pode ser um fator que pode ser potencialmente usado para classificar sua cesta de objetos de negociação.

• Fatores baseados em preços (indicadores técnicos): fatores baseados em preços, como discutido hoje, obtêm informações sobre o preço histórico de cada ação e o usam para gerar valores de fatores.

• Regressão e impulso: Vale a pena notar que alguns fatores acreditam que, uma vez que os preços se movem em uma direção, eles continuarão a fazê-lo, enquanto alguns fatores são exatamente o oposto.

• Fator básico (baseado no valor): Esta é uma combinação de valores básicos, como PE, dividendos, etc. O valor básico contém informações relacionadas com os fatos do mundo real da empresa, por isso pode ser mais poderoso do que o preço em muitos aspectos.

Em última análise, o preditor de desenvolvimento é uma corrida armamentista, e você está tentando ficar um passo à frente. fatores serão arbitragem do mercado e ter uma vida útil, então você deve trabalhar constantemente para determinar quantas recessões seus fatores experimentaram e quais novos fatores podem ser usados para substituí-los.

Outros aspectos

• Frequência de reequilíbrio

Cada sistema de classificação prevê retornos em um período de tempo ligeiramente diferente. A regressão média baseada no preço pode ser previsível em alguns dias, enquanto o modelo de fatores baseado no valor pode ser preditivo em alguns meses. É importante determinar o intervalo de tempo que o modelo deve prever e realizar verificação estatística antes de executar a estratégia.

• Capacidade de capital e custos de transacção

Cada estratégia tem o volume de capital mínimo e máximo, e o limiar mínimo é geralmente determinado pelo custo da transação.

A negociação de muitas ações levará a altos custos de transação. Se você quiser comprar 1.000 ações, custará milhares de dólares em cada reequilíbrio. Sua base de capital deve ser alta o suficiente para que os custos de transação possam representar uma pequena parte dos retornos gerados pela sua estratégia. Por exemplo, se seu capital for de US $ 100.000 e sua estratégia ganhar 1% ($ 1.000) por mês, todos esses retornos serão consumidos pelos custos de transação. Você precisa executar a estratégia com milhões de dólares de capital para ganhar mais de 1.000 ações.

O limite de ativos mais baixo depende principalmente do número de ações negociadas. No entanto, a capacidade máxima também é muito alta. A estratégia de equidade equilibrada de longo prazo pode negociar centenas de milhões de dólares sem perder a vantagem. Isso é um fato, porque essa estratégia é relativamente rara para reequilíbrio. O valor em dólares de cada ação será muito baixo quando os ativos totais são divididos pelo número de ações negociadas. Você não precisa se preocupar se seu volume de negociação afetará o mercado. Suponha que você negocie 1.000 ações, ou seja, 100.000.000 dólares. Se você reequilibrar todo o portfólio todos os meses, cada ação negociará apenas 100.000 dólares por mês, o que não é suficiente para ser um mercado importante para a maioria dos títulos.

Relacionados

Mais.