Формула Келли — мощный инструмент для контроля положения

** Предположим, что вы выиграли 60%, а проиграли 40%. Чистая прибыль при выигрыше составит 100%, а убыток при проигрыше составит 100%. То есть, если вы выиграете, то вы можете выиграть 1 доллар за 1 доллар, а если проиграете, то потеряете 1 доллар за 1 доллар.

• 1, для этой игры ожидаемая прибыль от каждой ставки составляет 60% от ставки*1-40%*1=20%, ожидаемая прибыль положительная. То есть, это тупик, в котором хакеры имеют преимущество, и преимущество очень большое.

Как же нам делать ставки?

Если мы не будем тщательно думать, то, грубо говоря, мы подумаем, что, поскольку я ожидаю 20% прибыли от каждой ставки, то для достижения максимальной прибыли в долгосрочной перспективе я должен постараться вложить как можно больше процентов капитала в каждую ставку.

Но очевидно, что вкладывать 100% капитала в каждую ставку является неразумным, потому что, как только любой игрок проиграет, все его капиталы будут потеряны, и он не сможет участвовать в следующей игре, а может просто уйти. В долгосрочной перспективе, проигрыш в игре неизбежен, поэтому в долгосрочной перспективе он неизбежно обанкротится.

И вот вывод: если есть вероятность, что в тупике можно потерять весь капитал сразу, даже если эта вероятность очень мала, то никогда не будет полного положения. Потому что в долгосрочной перспективе маловероятные события неизбежны, и в реальной жизни реальная вероятность маловероятного события намного больше, чем его теоретическая вероятность. Это - эффект “сапоги” в финансовой науке.

• 2 Продолжаем возвращаться к стадии 1. Если каждый раз ставить на 100% неразумно, то как же 99%. Если каждый раз ставить на 99% гарантированно никогда не обанкротится, а если повезет, то может получиться большая прибыль.

Это не то, что вы думаете, а то, что вы думаете.

Мы не будем анализировать эту проблему теоретически, мы сможем провести эксперимент. Мы смоделируем тупик, и каждый раз ставим 99 процентов, чтобы посмотреть, что получится.

Эксперимент был очень прост, и его можно было бы провести в Excel.

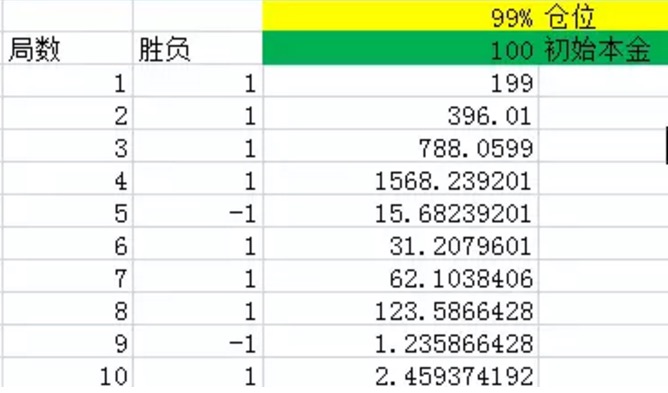Рисунок 1

На рисунке выше, первый столбец указывает количество игр. Второй столбец - выигрыш, Excel будет производить 1 с вероятностью 60%, то есть 60% вероятность чистой прибыли 1,40% вероятность -1, то есть 40% вероятность чистой прибыли -1. Третий столбец - все деньги в конце каждого игры.

Как видно из рисунка, после 10 игр, вероятность выигрыша в 10 игр составляет 8, а вероятность выигрыша в 10 игр больше, чем 60%, и вы проиграли всего два раза. Но даже в этом случае, у вас остается только 2.46 юаней, что в основном считается потерей.

Когда я увеличиваю количество экспериментов в тысячу, в двадцать, в тридцать раз, то, как вы можете себе представить, в конечном итоге деньги, которые я получаю, в основном, становятся нулевыми.

Поскольку 99% не работает, давайте попробуем еще несколько пропорций и посмотрим на график: Как видно из рисунка, если постепенно уменьшать позиции с 99%, до 90%, 80%, 70%, 60%, то результаты 10 игр будут совершенно разными. Из рисунка видно, что с постепенным уменьшением позиции, после 10 игр деньги постепенно увеличиваются.

Если вы посмотрите на это, то поймете, что проблема не в том, чтобы выиграть в тупике, а в том, чтобы выиграть в такой тупике, в которой игроки выигрывают, а не в тупике, в которой игроки выигрывают.

Как же тогда сделать ставку, чтобы получить максимальную отдачу в долгосрочной перспективе?

Как показан на рисунке выше, чем меньше, тем лучше? Не должно быть, потому что явно не получается зарабатывать деньги, когда соотношение становится 0.

Что же такое оптимальное соотношение?

Это проблема, которую нужно решить с помощью знаменитой формулы Келли!

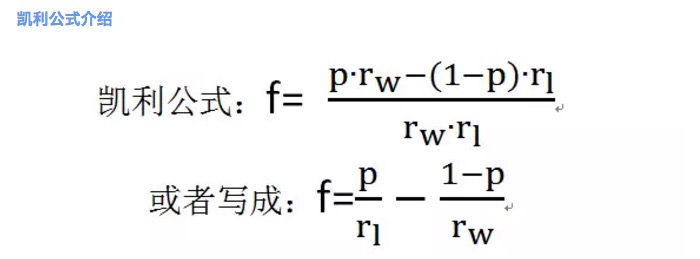Рисунок 2

где f - оптимальная ставка; p - вероятность выигрыша; rw - чистый доход при выигрыше, например, в туре 1; rl - чистый убыток при проигрыше, например, в туре 1; обратите внимание, что здесь rl > 0;

Согласно формуле Келли, можно вычислить, что максимальный процент ставки в туре 1 составляет 20%.

Мы можем провести эксперимент, чтобы лучше понять этот вывод.

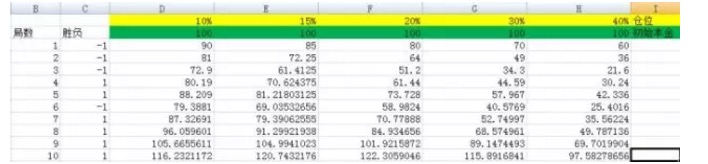Рисунок 3

Как показано на рисунке, мы устанавливаем позиции соответственно на 10%, 15%, 20%, 30%, 40% . Их соответствующие столбцы - D, E, F, G, H.

И когда я переводил эксперимент в 3000 раз, И когда я переводил это число в 5000 раз, я увидел, что у меня было больше возможностей. Из этого можно увидеть, что результат F-колонки является наибольшим, и корневой угол по сравнению с другими колонками не является количественным. А процент позиций F-колонки составляет 20%.

Вы видите силу формулы Келли. В эксперименте выше, если вы неудачно выбрали коэффициент 40%, то есть соответствующий H-колонке, то после 5000 игр, ваш капитал, хотя из 100 становится 22799985.75, прибыль огромная. Но по сравнению с результатом 20% коэффициента, это действительно равносильно тому, чтобы не заработать денег.

Это сила знаний!

• 3 Формула Келли

Математические выводы формулы Келли и их сложность требуют очень высокого и глубокого знания математики, поэтому здесь нет никакого смысла обсуждать их. Здесь я сделаю несколько экспериментов, чтобы углубить ваше понимание формулы Келли в субъективном плане.

Давайте посмотрим на лотерею. Лотерея 2: вероятность того, что вы проиграете и выиграете, составляет 50%, например, бросая монету. Чистая доходность при выигрыше равна 1, то есть rw = 1, а чистый убыток при проигрыше равен 0,5, то есть rl = 0,5. То есть, когда вы зарабатываете 1 доллар, вы выигрываете 1 доллар, а когда проигрываете, вы платите 5 мана.

Ожидаемая прибыль в тупике 2 составляет 0.25, и это тупик, в котором есть огромное преимущество для хакеров.

Согласно формуле Келли, мы получаем наилучший коэффициент ставки в игре:

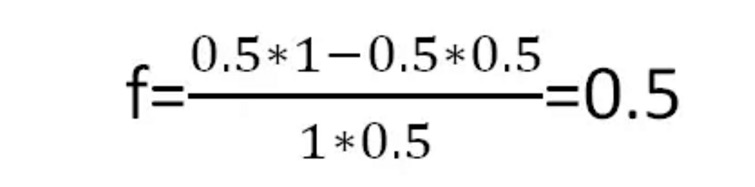Рисунок 4

Это означает, что каждый раз, когда вы ставите половину своих денег, вы получаете наибольшую прибыль в долгосрочной перспективе.

В следующем я выведу концепцию средней скорости роста r на основе экспериментов.

Вначале рассмотрим эксперимент 2.1, который включает в себя следующие две картинки:

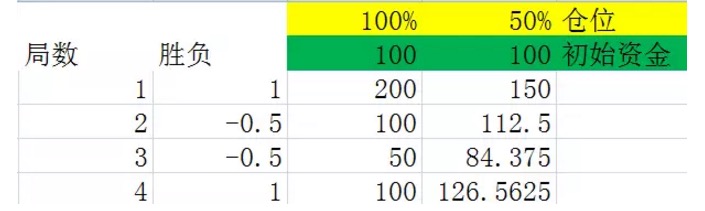Рисунок 5

Эти два диаграмма представляют собой эксперименты, выполненные при моделировании игры в тупик 2, в котором вторая строка с выигрышной строкой дает 50% вероятность того, что эксперимент получит 1, что означает 100% прибыли. 50% вероятность -0,5, что означает 50% убытков. Третья и четвертая строки представляют собой средства, которые вы имеете после каждой игры в тупик под позициями 100% и 50% соответственно.

Если тщательно сравнить эти две карты, то можно сделать вывод, что после того, как вы прошли одинаковое количество туров, конечный результат связан только с количеством выигранных туров и количеством проигранных туров в этих числах, а не с последовательностью выигранных туров и проигранных туров в этих числах. Например, в предыдущих двух картах также проводились 4 тура, также в каждом из них было два выигранных тура.

Конечно, этот вывод очень легко доказать (закон смены умножения, это знают школьники), но здесь это не доказано, и выше приведенных примеров достаточно, чтобы все хорошо поняли.

Итак, поскольку окончательный результат не зависит от того, в каком порядке выигрыш или проигрыш, мы предполагаем, что фиаско 2 будет выполняться так же, как и в эксперименте 2.2.

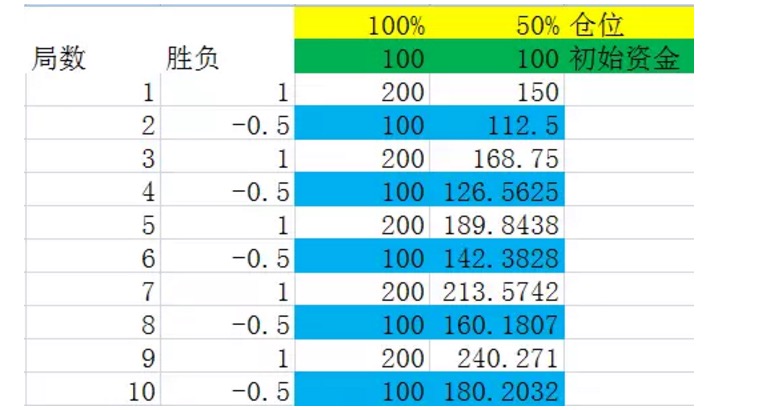Рисунок 6

Мы предполагаем, что выигрыш в тупике происходит поочередно, и, поскольку вывод 1, в долгосрочной перспективе это не имеет никакого влияния на финансовые результаты.

Перед тем как посмотреть на картинку, давайте сделаем определение. Предположим, что мы рассматриваем нескольких тупиков как целое, в котором частота различных результатов равна их вероятности, и количество тупиков в этом целом является наименьшим из всех удовлетворяющих условиям. Тогда мы называем это целое группой тупиков. Например, в эксперименте на рисунке выше, группа тупиков представляет собой два тупика, каждый из которых выигрывает и проигрывает.

Если внимательно посмотреть на цифры, отмеченные синим цветом на диаграмме выше, они являются концами группы тупиков. Вы увидите, что эти цифры стабильно растут. Когда позиция составляет 100%, рост числа, отмеченного синим цветом, составляет 0%, то есть рост капитала после группы тупиков составляет 0%. Это также объясняет, что каждый раз, когда все позиции заполнены, в среднесрочной перспективе в тупике 2 невозможно заработать.

Это общепринятый закон, что рост после каждой паузы связан с позицией. И чем больше рост после каждой паузы, тем больше будет конечная прибыль в долгосрочной перспективе.

В зависимости от темпов роста каждой группы застоя можно вычислить средний темп роста каждой застоя g. На рисунке выше, если в каждой группе застоя содержится две застоя, то средний темп роста каждой застоя

Рисунок 7

В долгосрочной перспективе, чтобы добиться максимального роста капитала, нужно максимально увеличить r, то есть максимально увеличить g. И оптимальный коэффициент ставки f, на самом деле, выводится из решения max (g).

• 4. Другие выводы по формуле Келли о рисках

Легенда о Келли

Формула Келли была первоначально создана для физика AT&T Bell Labs Джона Ларри Келли на основе исследований его коллеги Клода Элвуда Шэнона о переписке на дальних телефонных линиях. Келли решил проблему того, как теория информации Шэнона должна применяться к игроку, который владеет внутренней информацией, во время игры в кости. Он использовал свои знания, чтобы за одну ночь нанести удар по всем казино в Невадарено и выиграть десятки тысяч долларов на столе с 21 игрой. Он также был прародителем американского хедж-фонда количественной торговли на Уолл-стрит, который в 1970-х годах создал первый хедж-фонд количественной торговли.

Использование перспективы

Как можно использовать формулу Келли, чтобы зарабатывать деньги в реальной жизни? Это означает, что мы должны создать тупик, который будет соответствовать условиям, предъявляемым к формуле Келли. В последнее время я занимаюсь исследованием торговых систем, и что самое важное для хорошей торговой системы? Ожидаемый положительный доход, правила торговли и купли составляют 10% от важности, а хороший метод управления капиталом составляет 40% от важности, а остальные 50% - это психологический контроль над людьми. Именно формула Келли помогла мне контролировать мои финансовые позиции. Например, одна система торговли акциями, которую я исследовал ранее, проводила одну неделю, вероятность успешной торговли составляла 0,8, вероятность неудачи составляла 0,2%. Когда удалось, можно было заработать 3% (за вычетом комиссии, налога на отпечаток), а при каждой неудаче - потерять 5%. Разумеется, формула Келли не может быть такой простой в практическом применении, и есть много трудностей, которые необходимо преодолеть. Например, стоимость капитала, необходимая для лейб-бирж, например, в реальности средства не являются бесконечно делящимися, например, на финансовых рынках не так просто, как упомянутая выше простая тупик. Но в любом случае, формула Келли указывает нам путь вперед.