Скрытая марковская модель

• ### Знакомство

Сегодня мы расскажем о простом применении модели HMM в акциях.

Если мы не знаем, что такое цепь Маркова, то давайте сделаем шаг назад и посмотрим на цепь Маркова.

Марковская цепь, названная в честь Андрея Маркова (А. А. Маркова, 1856-1922), - это случайная последовательность отдельных событий, обладающих марковским характером в математике. В данном случае текущего знания или информации прошлое (то есть историческое состояние до настоящего) не имеет отношения к прогнозированию будущего (то есть будущее состояние после настоящего).

Процесс, при котором перемещение каждого состояния зависит только от предыдущих n состояний, называется моделью с 1 n степеней, где n - количество влияющих на перемещение состояний. Самый простой марковский процесс - это одноступенчатый процесс, при котором перемещение каждого состояния зависит только от предыдущего.

• ### Пример 2.

В математическом выражении это выглядит следующим образом:

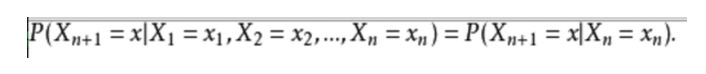
В качестве примера из повседневной жизни, мы хотим предсказать будущее погодные условия на основе текущей погоды. Один из способов - предположить, что каждое состояние модели зависит только от состояния предыдущего, то есть Марковская гипотеза, которая может значительно упростить эту проблему. Конечно, этот пример также является несколько непрактичным. Однако такая упрощенная система может быть полезна для нашего анализа, поэтому мы обычно принимаем такие гипотезы, потому что мы знаем, что такая система может дать нам некоторую полезную информацию, хотя и не очень точная.

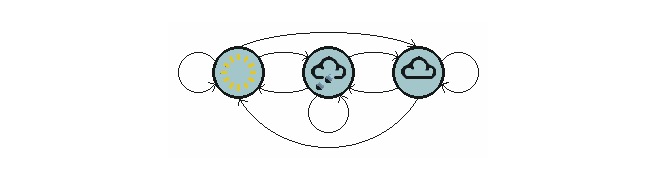
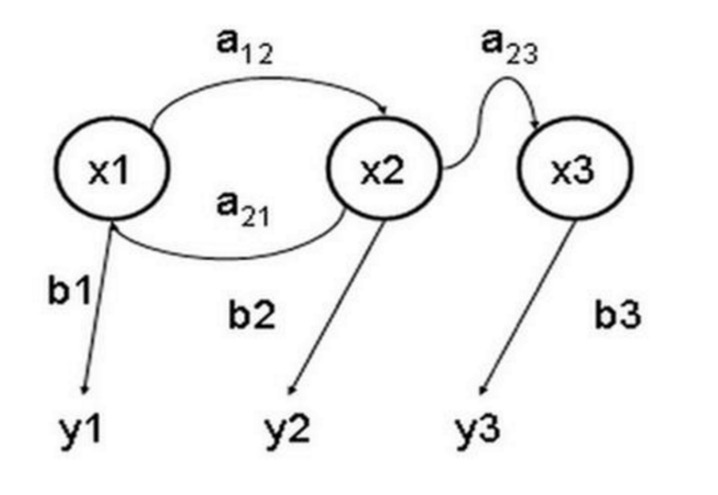
На рисунке выше показана модель переноса погоды.

Заметьте, что в процессе одного этапа, содержащем N состояний, есть N2 преобразований состояния. Вероятность каждого преобразования называется вероятностью преобразования состояния, то есть вероятностью преобразования из одного состояния в другое. Все эти N2 вероятности могут быть представлены матрицей преобразований состояния.

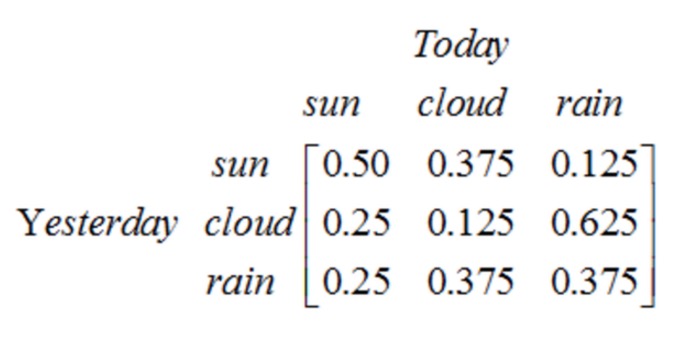
Эта матрица показывает, что если вчера было облачно, то сегодня с вероятностью 25% будет солнечно, с вероятностью 12.5% будет облачно, с вероятностью 62.5% будет дождь. Очевидно, что сумма каждой строки в матрице равна 1.

Для того, чтобы инициировать такую систему, нам нужен первоначальный вектор вероятности:

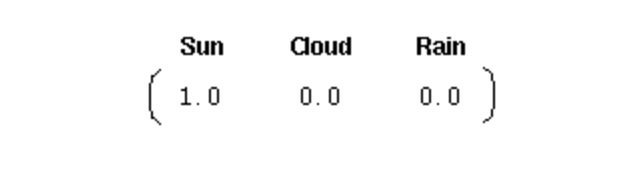
Этот вектор показывает, что первый день был солнечным. Здесь мы определяем три части для вышеуказанного первого этапа Марковского процесса:

Ситуация: солнечная, пасмурная и дождливая.

Первоначальный вектор: вероятность состояния системы, когда время 0

Матрица перехода состояний: вероятность каждого перехода погоды. Все системы, которые могут быть описаны таким образом, являются процессами Маркова.

Однако, что делать, если процесс Маркова не является достаточно мощным? В некоторых случаях он недостаточно хорош, чтобы описать модель, которую мы хотим обнаружить.

Например, наш фондовый рынок, если только наблюдать за рынком, мы можем знать только цены, объемы торгов и т. Д., Но не знаем, какое состояние в данный момент на фондовом рынке ((бычьи, медные, колебания, отскок и т. Д.), В этом случае у нас есть два набора состояний, набор состояний, которые можно наблюдать (набор состояний цены и торгов на фондовом рынке и т. Д.) и набор состояний, которые скрыты (набор состояний на фондовом рынке). Мы надеемся найти алгоритм, который может прогнозировать состояние фондового рынка на основе цены и торгов на фондовом рынке и предположения Маркова.

В этих случаях последовательность наблюдаемого состояния и последовательность скрытого состояния связаны вероятностью. Таким образом, мы можем смоделировать этот тип процесса как имеющий скрытый процесс Маркова и совокупность состояний, связанных с вероятностью этого скрытого процесса Маркова и наблюдаемых, то есть модель скрытого Маркова.

Скрытая марковская модель (англ. Hidden Markov Model) - это статистическая модель, используемая для описания марковского процесса, содержащего неизвестные параметры. Трудность заключается в том, чтобы определить скрытые параметры процесса из наблюдаемых параметров, а затем использовать эти параметры для дальнейшего анализа.

Для иллюстрации приведем пример с яблоком. Предположим, что у меня в руках три разных яблока. Первый яблоко - это обычный яблоко (назовем его D6), 6 сторон, каждая сторона (назовем его 1, 2, 3, 4, 5, 6) имеет вероятность ¹⁄₆.

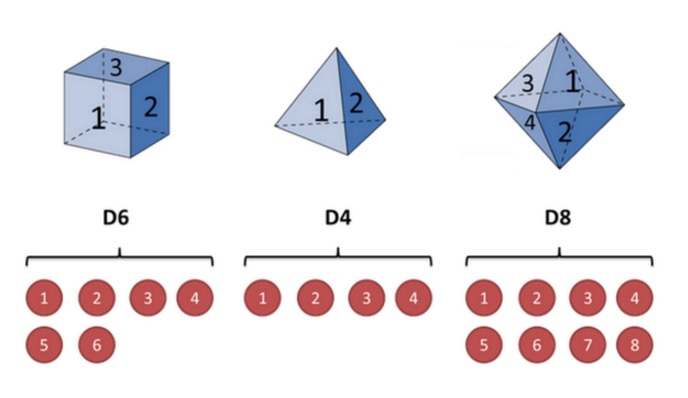
Предположим, что мы начинаем выбирать из трёх ящиков, и вероятность выбора каждого ящика равна ¹⁄₃. Затем мы выбираем число 1, 2, 3, 4, 5, 6, 7, 8. Повторяя этот процесс, мы получаем ряд чисел, каждый из которых является одним из 1, 2, 3, 4, 5, 6, 7, 8.

Эта строка чисел называется цепью видимых состояний. Но в подпольной марковской модели у нас есть не только такая строка видимых состояний, но и цепь скрытых состояний. В этом примере, эта цепь скрытых состояний - это последовательность палочек, которые вы используете.

В общем случае, Марковская цепь, о которой говорится в HMM, на самом деле является цепью скрытых состояний, поскольку между скрытыми состояниями ([[кольцо]]) существует вероятность преобразования. В нашем примере следующее состояние D6 - D4, D6, вероятность преобразования D8 - ¹⁄₃. Следующее состояние D4, D8 - D4, D6, D8 - ¹⁄₃ вероятность преобразования.

Точно так же, несмотря на то, что между видимыми состояниями нет вероятности преобразования, между скрытыми состояниями и видимыми состояниями есть вероятность, называемая вероятностью выхода. В нашем примере, вероятность выхода 1 из шестигранной коробки (D6) составляет ¹⁄₆. Вероятность выхода 2, 3, 4, 5, 6 также составляет ¹⁄₆.

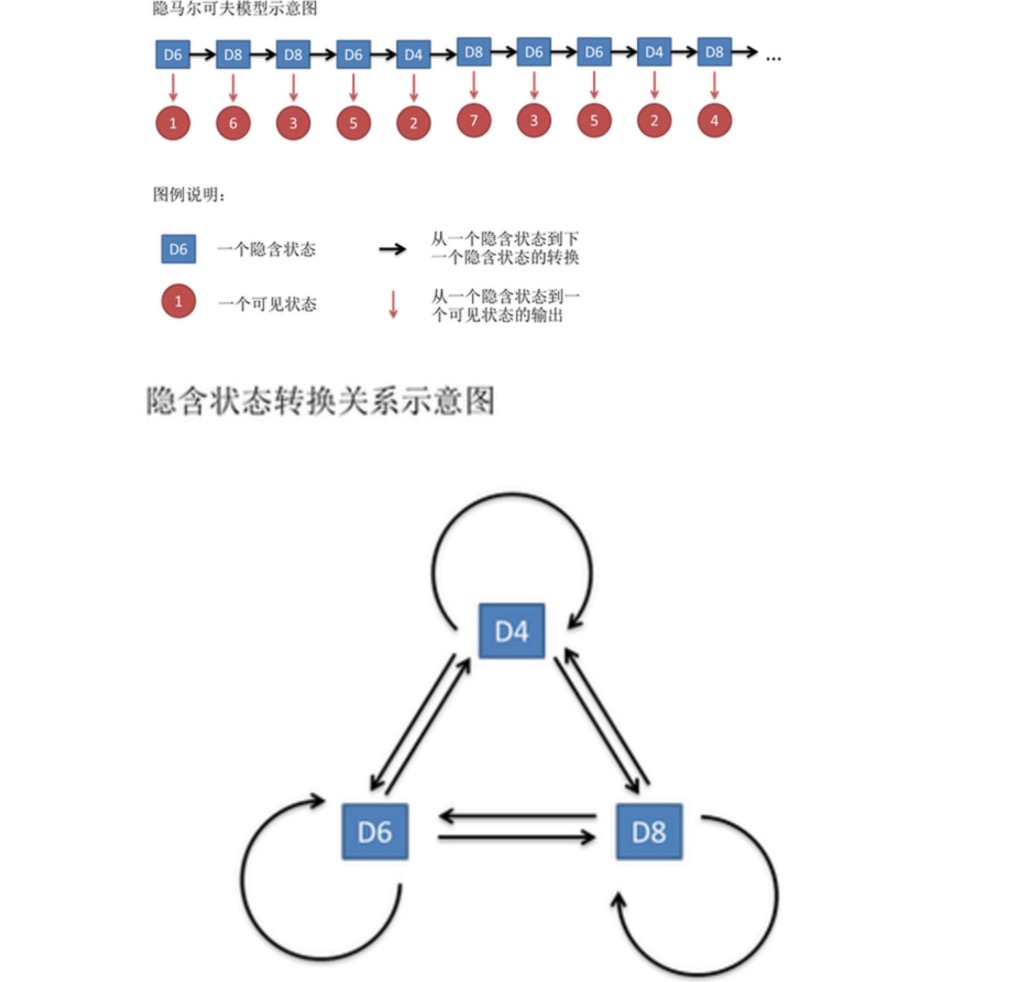
В действительности, для HMM, если заранее знать вероятность преобразования между всеми скрытыми состояниями и вероятность вывода между всеми скрытыми состояниями и всеми видимыми состояниями, сделать моделирование довольно легко. Но при применении модели HMM, часто часть информации отсутствует, иногда вы знаете, сколько есть ячейки, что такое каждая ячейка, но не знаете, какая последовательность ячейки вышла; иногда вы просто видите результаты ячейки много раз, а остальное ничего не знаете.

Алгоритмы, связанные с моделью HMM, подразделяются на три основные категории, решающие три проблемы:

• Знать, сколько есть контактов ((количество скрытых состояний), что такое каждый контакт ((вероятность преобразования), в зависимости от результатов выбора контактов ((видимая цепочка состояний), я хотел бы знать, какой контакт выбирается каждый раз ((цепочка скрытых состояний)).

• Я также хочу знать, сколько контактов существует (количество скрытых состояний), какова вероятность каждого контакта (вероятность преобразования) и вероятность получения этого результата в зависимости от результатов, полученных контактом (череда видимых состояний).

• Зная, что существует несколько типов ящериц (количество скрытых состояний), не зная, что такое каждая ящерица (вероятность преобразования), наблюдая за результатами многих ящериц (видимая цепь состояний), я хотел бы вывести, что такое каждая ящерица (вероятность преобразования).

  Если мы хотим решить эти проблемы, нам нужно решить вопросы 1 и 3, и в следующей статье мы увидим, как это сделать.

Копировано из колонки Unknown Moneycode