Сегодня я хочу поделиться с вами стратегией, которую используют туземцы в последнее время (doge). I. Предпосылки Классические стратегии выбора времени на самом деле делятся на несколько основных категорий: краткосрочные события (наблюдение за объявлениями и твитами на крупных биржах, связанные с текстовым анализом), статистическая регрессия и прогнозирование (статистический арбитраж, параллельные сделки, различные типы моделей ML и DL, маркировка Маркова и т. д.), выбор эмоций инвесторов в классе GSISI и традиционные классические технические показатели.

N日移动平均线=N日收盘价之和/N

Это то, что большинство инвесторов обычно называют средней линией (MA), средняя линия, которая пробивается, покупается, продается, и многое другое.*Ная вносит свой вклад в расходы на биржу. Однако у обычных инвесторов есть несколько проблем с использованием средней линии: во-первых, средняя линия является серьезной задержкой, и, как правило, когда появляется сигнал, тенденция уже почти закончена, и они возвращаются; во-вторых, обычные инвесторы в криптовалюту, как правило, обращаются к показателям на уровне минут, 15 мин, 5 мин и даже 1 мин, более 80% криптовалюты в таком небольшом периоде характеризуются колебаниями (такие, как Мартин), тенденции редко происходят, и инвесторы, открывающие позиции в соответствии со средней линией, теряют большое количество просрочных сборов и сбоев. ● Целью данного материала является создание алгоритма для фильтрации и снижения задержек в отношении среднелинейных индикаторов, который будет доступен для всеобщего использования.

Z-образование, передающая функция ● До этого статьи я узнал о некоторых алгоритмах, используемых для измерения показателей, таких как наиболее распространенные кристаллические волны (появляющиеся в нескольких изданиях Squirrel Compassionate CTA), а также о методе Кальмана, который был разработан автором на joinquant, который в ретроспективе успешно избежал катастрофы 2015 года. ● Z преобразование от Лапласа, часто используется в области математической обработки сигналов. Для дифференцированной временной последовательности f ((k) и z, определенной в двойном частотном поле, его формула определяется следующим образом:

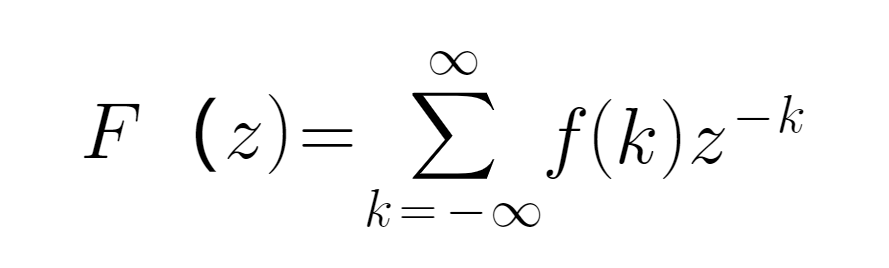
● средняя линия EMA имеет меньшую задержку по сравнению с MA ((сущность является результатом обработки последовательности MA с помощью алгоритма EWMA), поэтому мы здесь используем последовательность EMA, а не MA, что улучшает эффект фильтрации. Мы определяем входную величину как цену валюты ((завершающая цена), записанную как p ((z), а выходную величину как и соответствующий показатель EMA, записанный как ((EMAz)), поэтому передающая функция в этой сущности является EMA валюты и соотношение интенсивности ее соответствующей завершающей цены, которая является системой обратной связи, с передающей функцией H ((z), тогда:

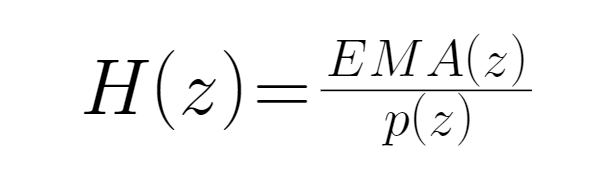
● Введение этой формулы в алгоритм EWMA дает первоначальную передаточную функцию EMA:

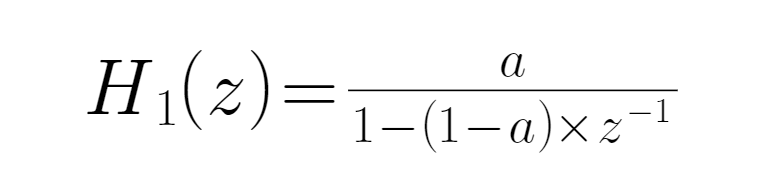
● где a - переменный параметр, следующий ≠

1. Анализ передающей функции ● В передаваемой функции входный сигнал не связан с значениями функций.При -1=-1 H(z) принимает максимальное значение, то есть достигает максимальной частоты, передаваемая функция H(z) = a/(2-a, и шум с недавних высокочастотных данных максимально ослабляется; когда zКогда H{\displaystyle \mathbb {Z} } -1=1 и систематическая частота равна нулю, ввод и вывод одинаковы. Если временная последовательность в данный момент является постоянной, то значение EMA будет совпадать. ● Когда H(z) является низкопроницаемым фильтром, а H(z) = 1, то выходный сигнал включает в себя все доли входного сигнала, то есть из всего выходного сигнала, если вычесть все низкочастотные сигналы, 1-H(z) может быть сконструирован в новый фильтр, записанный как H’(z), в точности наоборот, чем H(z), который является высокопроницаемым фильтром. ●Запишите P (T) как цену в корневой k-линии, чтобы сгладить эту функцию, мы берем цену на день и цену на день ранее, чтобы сделать дальнейшую коррекцию выходной EMA (это потому, что при первоначальной передаче функции H (z) = a/ (-2-a) высокочастотный сигнал не был эффективно отфильтрован, поэтому для сглаживания принимается предыдущее значение, и если эффект не является хорошим, можно взять несколько нагрузок), поэтому коррекция EMA на день ввода выражена следующим образом: 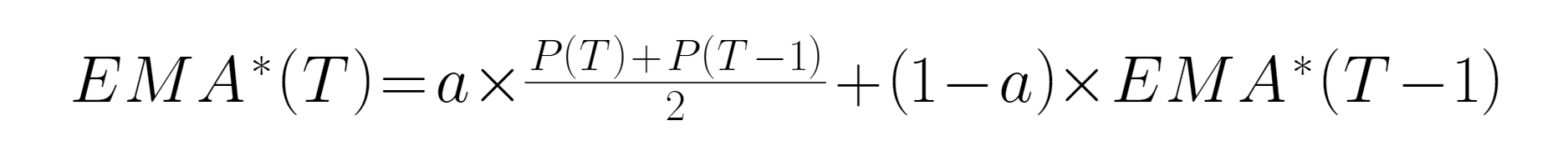● Для фильтра с низким уровнем пропускания выражение фильтра с высоким уровнем пропускания требует только уменьшения его на 1: 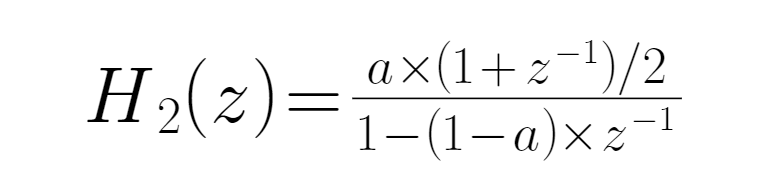● Теперь выражение фильтра уже построено! С помощью Z-образования мы можем построить трендовую линию с низкой задержкой, и она имеет только один параметр a, чем больше a, тем меньше задержка, и тем лучше плавность. Для разных сортов существуют различные оптимальные параметры.

2. Резюме и примечания ● Фильтр, построенный в вышеуказанном шаге, имеет только одну ступень, из-за длины переходного ряда его эффект фильтрации не является очень идеальным, а после повышения степени сложность выражения функции H’{\displaystyle H’{\displaystyle z}) показывает показательный рост, слишком высокие степени также подвержены нерегулярным прыжкам в равновесии фильтрации. По опыту, 2 или 3 ступень являются более подходящими степенями, читатель может также самостоятельно использовать линейную комбинацию, чтобы соединить в последовательности несколько однородных или разных степеней фильтрации наблюдателей их эффекта, поскольку автор был занят своими делами, и не мог проверить их экспериментально. ● Этот алгоритм фильтрации, основанный на преобразовании Z, применим не только к показателям средней линейной категории, но и ко всем показателям с ложными сигналами, таким как Boll и ATR, благодаря алгоритму фильтрации можно достичь определенного эффекта фильтрации, определить размер прорыва порога открытия позиции, что снижает уровень задержки основного показателя. В этой статье, в конце статьи, мы не будем предоставлять коды соответствующих алгоритмов, а просто дадим представление, которое заинтересованные читатели могут попробовать сами.

●Promise Quant Мино специализируется на разработке различных стратегий фантастических туземных собак, основанных на Мартине, например, если у вас есть потребности в аренде или большие потребности в управлении капиталом, свяжитесь с vx: 15001733415