Коэффициент Шарпа 0,6, стоит ли от него отказаться?

Мы провели эксперимент, чтобы проиллюстрировать эту проблему. Эксперимент начался с нескольких ключевых допущений. У нас было 20 торговых сигналов, которые имели годовой комбинированный доход 8% и годовой соотношение Шарп 0.6.

• Важной входной переменной в трейдинге является корреляция между сигналами. Мы проводим ряд экспериментов с коэффициентом корреляции от 0 до 0.9. Эксперименты не учитывают стоимость трейдинга (поскольку нас интересует только относительная эффективность), и распределение доходности годового портфеля, сбалансированного ежедневно в соответствии с корреляцией, в основном одинаково.

  

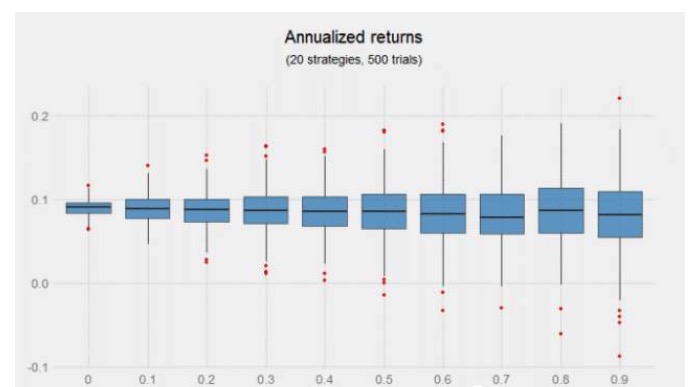
  Объединение сигналов с низкой корреляцией не повышает доход, но приведенная выше диаграмма намекает на возможные преимущества увеличения стратегий, особенно в случае, когда эти стратегии не связаны. Левая половина диаграмма, то есть коэффициент корреляции от 0 до 0,4, имеет более узкое распределение, и доход от пятисот экспериментов является положительным.

  Результаты эксперимента более ясны, когда используется коэффициент Шарпа для измерения риск-регулируемой прибыли. 20 стратегий с годовым коэффициентом Шарпа 0,6 и коэффициентом взаимосвязи 0, создают комбинацию с годовым коэффициентом Шарпа 3, в то время как 20 стратегий с годовым коэффициентом Шарпа 0,6 и коэффициентом взаимосвязи 0,9 создают комбинацию с годовым коэффициентом Шарпа 0,64, причем первые приносят прибыль на 370% больше, чем последние.

  

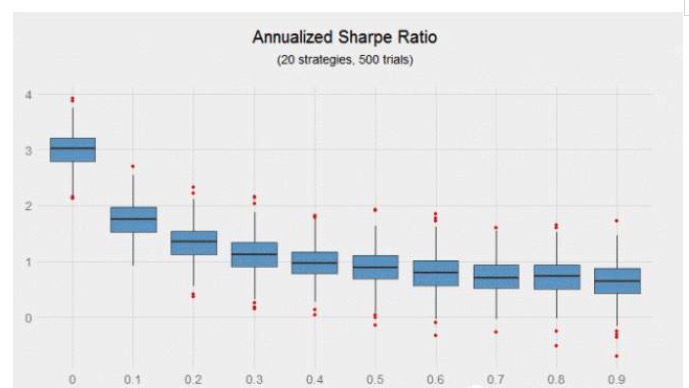
  Примечательно, что по мере повышения корреляции стратегии коэффициент Шарпа снижается очень быстро. Коэффициент корреляции увеличивается с 0 до 0.2, а коэффициент Шарпа снижается на 56%.

  Несмотря на высокий коэффициент Шарпа, этот портфель имеет почти 50000 торговых сигналов, разница в коэффициенте Шарпа в портфеле с нулевой корреляцией поразительна. Счастливый инвестор может получить коэффициент Шарпа 3,5 (может сделать человека миллиардером), а несчастный инвестор с таким же портфелем получает коэффициент Шарпа 2,5. Даже в портфеле с высоким коэффициентом Шарпа удача играет важную роль.

  Несмотря на 5000 сделок, большинство инвестиционных портфелей связаны с элементом случайности. Это, очевидно, является причиной того, что хедж-фонды, управляемые данными, предпочитают высокочастотные сделки, поскольку высокочастотные сделки быстрее проверяют сигналы и достигают среднего значения своего показателя.

  

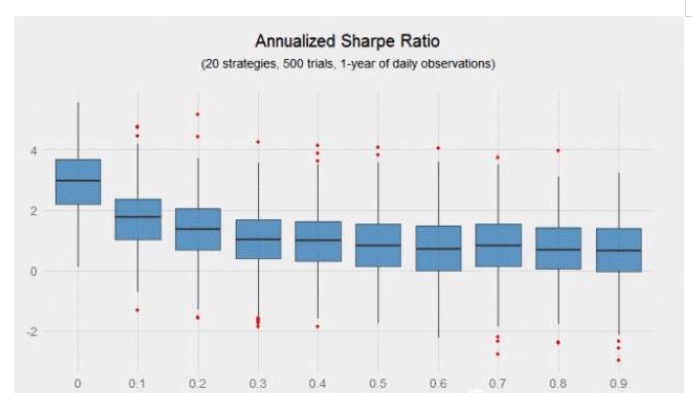
  Если мы смоделируем 10000 отдельных стратегий выше, какая доля p-значений будет меньше 5%? Ответ - около 48%, что может привести к тому, что большинство исследователей откажутся от такой повседневной стратегии (т.е. стратегии с годовым коэффициентом Шарпа 0,6). Однако, если корреляция между сигналами достаточно низка, то объединение этих слабых сигналов может произвести чудеса, и поток прибыли от комбинации станет очень значительным.

  

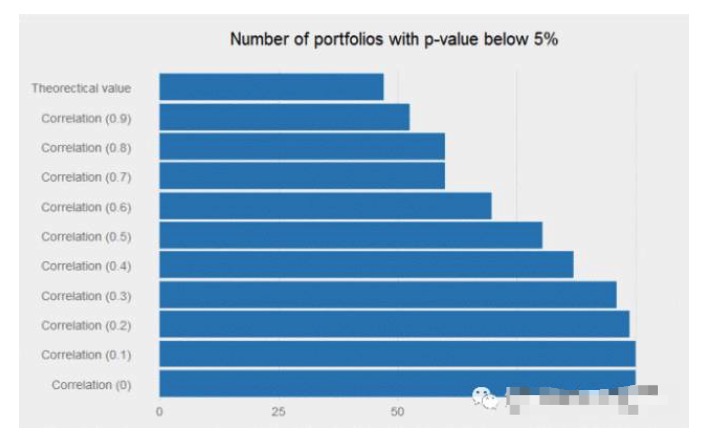
  Стратегия с годовым коэффициентом Шарпа 0,6 может быть отброшена исследователями, поскольку не имеет никакой привлекательности в торговле. Однако, если она имеет правильную (т.е. низкую) корреляцию между существующими сигналами, то она может значительно увеличить стоимость портфеля.

  В этой статье не открывается новая область, потому что преимущества дифференцированного инвестирования хорошо известны в инвестиционном сообществе. Но это действительно напоминает вам, что вам не нужно отказываться от стратегии с годовым коэффициентом Шарпа 0,6. Возможно, вы можете добавить его в свой существующий портфель стратегий, что снизит ликвидность портфеля и позволит использовать больше рычагов для повышения общей прибыли.

Переводчик: