Мощный инструмент для программатических трейдеров: алгоритм дополнительного обновления для расчета среднего и варианта

Введение

В программируемой торговле часто необходимо вычислять средние и варианты, такие как вычисление скользящих средних и показателей волатильности. Когда нам нужны высокочастотные и долгосрочные вычисления, необходимо долгое время сохранять исторические данные, что является как ненужным, так и ресурсоемким. В этой статье представлен алгоритм онлайн-обновления для вычисления взвешенных средних и вариантов, который особенно важен для обработки потоков данных в режиме реального времени и динамической корректировки торговых стратегий, особенно высокочастотных.

Простая средняя и вариантность

Если мы используем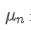чтобы представить среднее значение nth точки данных, предполагая, что мы уже рассчитали среднее число n-1 точек данных /upload/asset/28e28ae0beba5e8a810a6.png, теперь мы получаем новую точку данных /upload/asset/28d4723cf4cab1cf78f50.png. Мы хотим рассчитать новое среднее число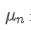Ниже приведена подробная выводка.

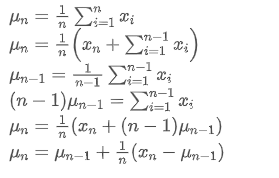
Процесс обновления дисперсии может быть разделен на следующие этапы:

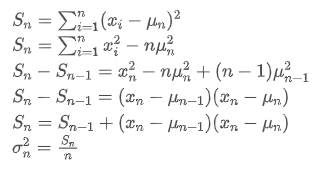
Как видно из двух вышеприведенных формул, этот процесс позволяет нам обновлять новые средние значения и варианты при получении каждой новой точки данных.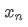Однако проблема заключается в том, что то, что мы рассчитываем таким образом, это среднее значение и вариантность всех образцов, в то время как в реальных стратегиях нам нужно учитывать определенный фиксированный период. Наблюдение за вышеуказанным средним обновлением показывает, что количество новых средних обновлений - это отклонение между новыми данными и прошлыми средними значениями, умноженное на соотношение. Если это соотношение будет фиксировано, это приведет к экспоненциально взвешенному среднему значению, которое мы обсудим далее.

Экспоненциально взвешенное среднее значение

Экспоненциальное среднее значение может быть определено следующей рекурсивной связью:

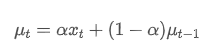
Среди них,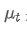это экспоненциальное среднее значение в момент t,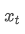является наблюдаемым значением в момент t, α - весовой коэффициент, и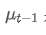это экспоненциальное среднее значение предыдущей точки времени.

Экспоненциально-взвешенная вариантность

Что касается вариантности, нам нужно вычислить экспоненциальное среднее значение квадратных отклонений в каждый момент времени. Это можно достичь с помощью следующей рекурсивной связи:

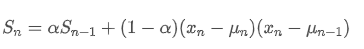
Среди них,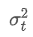экспоненциально взвешенная вариация в момент t, и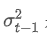это экспоненциально взвешенное расхождение предыдущей точки времени.

Наблюдайте за экспоненциально взвешенной средней величиной и вариантом, их инкрементальные обновления интуитивно понятны, сохраняя часть прошлых значений и добавляя новые изменения.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA и EMA

SMA (также известный как среднее арифметическое значение) и EMA - это две общие статистические меры, каждая из которых имеет различные характеристики и применения. Первая присваивает равное значение каждому наблюдению, отражая центральное положение набора данных. Последняя является рекурсивным методом расчета, который придает более высокий вес более поздним наблюдениям.

• Распределение веса: SMA придает один и тот же вес каждой точке данных, в то время как EMA придает более высокий вес самым последним точкам данных.
• Чувствительность к новой информации: SMA недостаточно чувствителен к новым данным, поскольку он предполагает перерасчет всех точек данных.
• Вычислительная сложность: Расчет SMA относительно прост, но по мере увеличения числа точек данных увеличивается и расчетная стоимость.

Приблизительный метод преобразования между EMA и SMA

Хотя SMA и EMA концептуально отличаются, мы можем сделать EMA приблизительным к SMA, содержащему определенное количество наблюдений, выбрав соответствующее значение α. Эта приблизительная связь может быть описана эффективным размером выборки, который является функцией весового фактора α в EMA.

SMA - это среднее число всех цен в течение определенного периода времени. Для периода времени N центроид SMA (т.е. положение, где находится среднее число) можно рассматривать как:

центроид SMA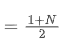

EMA - это тип взвешенной средней, где самые последние точки данных имеют больший вес. Вес EMA уменьшается экспоненциально с течением времени. Центроид EMA можно получить путем суммирования следующих рядов:

центроид EMA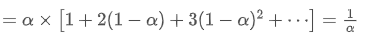

Если предположить, что SMA и EMA имеют один и тот же центроид, мы можем получить:

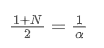
Чтобы решить это уравнение, мы можем получить отношение между α и N.

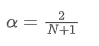
Это означает, что для заданной SMA длительностью N дней соответствующее значение α может быть использовано для расчета эквивалентной EMA, так что они имеют один и тот же центроид и результаты очень похожи.

Преобразование EMA с различной частотой обновления

Предположим, что у нас есть EMA, которая обновляется каждую секунду, с коэффициентом веса /upload/asset/28da19ef219cae323a32f.png. Это означает, что каждую секунду в EMA будет добавляться новая точка данных с весом /upload/asset/28da19ef219cae323a32f.png, в то время как влияние старых точек данных будет умножено на /upload/asset/28cfb008ac438a12e1127.png.

Если мы изменяем частоту обновления, например, обновление раз в f секунд, мы хотим найти новый весовой коэффициент /upload/asset/28d2d28762e349a03c531.png, так что общее влияние точек данных в пределах f секунд такое же, как при обновлении каждую секунду.

В течение f секунд, если обновления не будут выполнены, влияние старых точек данных будет непрерывно уменьшаться в f раз, каждый раз умножаясь на /upload/asset/28e50eb9c37d5626d6691.png. Таким образом, общий коэффициент упадка после f секунд составляет /upload/asset/28e296f97d8c8344a2ee6.png.

Для того, чтобы EMA, обновляемая каждые f секунд, имела такой же эффект распада, как EMA, обновляемая каждую секунду в течение одного периода обновления, мы устанавливаем общий коэффициент распада после f секунд равный коэффициенту распада в течение одного периода обновления:

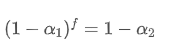
Разрешая это уравнение, мы получаем новые весовые факторы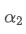

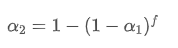
Эта формула дает приблизительное значение нового весового коэффициента /upload/asset/28d2d28762e349a03c531.png, который сохраняет эффект сглаживания EMA неизменным при изменении частоты обновления.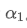с значением 0,001 и обновлять его каждые 10 секунд, если он изменяется на обновление каждую секунду, эквивалентное значение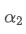будет приблизительно 0,01.

Внедрение кода Python

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Резюме

В высокочастотной программируемой торговле быстрая обработка данных в режиме реального времени имеет решающее значение. Для повышения вычислительной эффективности и сокращения потребления ресурсов в этой статье представлен алгоритм онлайн-обновления для непрерывного расчета взвешенной средней и вариантности потока данных. Инкрементальные обновления в режиме реального времени также могут использоваться для различных статистических данных и расчетов индикаторов, таких как корреляция между двумя ценами активов, линейное соответствие и т. д., с большим потенциалом. Инкрементальное обновление рассматривает данные как систему сигналов, что является эволюцией в мышлении по сравнению с расчетами фиксированного периода. Если ваша стратегия все еще включает в себя части, которые рассчитывают с использованием исторических данных, подумайте о преобразовании ее в соответствии с этим подходом: записывайте только оценки состояния системы и обновляйте состояние системы при поступлении новых данных; повторяйте этот цикл в будущем.