Измерение риска и доходности — Введение в теорию Марковица
 0
0
 1635
1635

На прошлой неделе мы представилиУправление рисками VaRКогда речь идет о риске портфеля, он не равен риску каждого отдельного актива, а связан с их ценовой корреляцией. Возьмем в качестве примера два актива, если их положительная корреляция очень сильна, то есть они растут и падают вместе, то диверсификация длинных инвестиций не снизит риск. Если отрицательная корреляция очень сильна, диверсификация может значительно снизить риск. Возникает естественный вопрос: как при инвестировании в портфель максимизировать доходность при определенном уровне риска? Вот здесь-то и вступает в игру теория Марковица, которую я сегодня представлю.
Современная теория портфеля (MPT), предложенная Гарри Марковицем в 1952 году, представляет собой математическую основу для выбора портфеля, целью которой является максимизация ожидаемой доходности путем выбора различных комбинаций рискованных активов. прибыли при одновременном контроле рисков. Основная идея заключается в том, что цены на активы не движутся идеально синхронно (т. е. между активами существует несовершенная корреляция), и общий инвестиционный риск можно снизить за счет диверсификации распределения активов.
Ключевые концепции теории Марковица
- Ожидаемая норма прибыли: Это доход, на который инвестор может рассчитывать, владея активом или портфелем, обычно прогнозируемый на основе исторических данных о доходности.
\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)
Где \(E(R_p)\) — ожидаемая норма доходности портфеля, \(wi\) — вес \(i\)-го актива в портфеле, а \(E(R_i)\) — ожидаемая норма доходности \( i\)й актив. .
- Риск (волатильность или стандартное отклонение): Используется для измерения неопределенности доходности инвестиций или волатильности инвестиций.
\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)
Где \(\sigma_p\) — общий риск портфеля, а \(\sigma_{ij}\) — ковариация между активом \(i\) и активом \(j\), которая измеряет взаимосвязь между изменениями цен двух активов.
- Ковариация: Измеряет корреляцию между изменениями цен двух активов.
\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)
Где \(\rho_{ij}\) — коэффициент корреляции между активом \(i\) и активом \(j\), \(\sigma_i\) и \(\sigma_j\) — стандартные отклонения актива \(i\) и актива \(j\) соответственно.
- Эффективная граница: В системе координат «риск-доходность» эффективная граница — это набор портфелей, которые могут обеспечить максимальную ожидаемую доходность при заданном уровне риска.
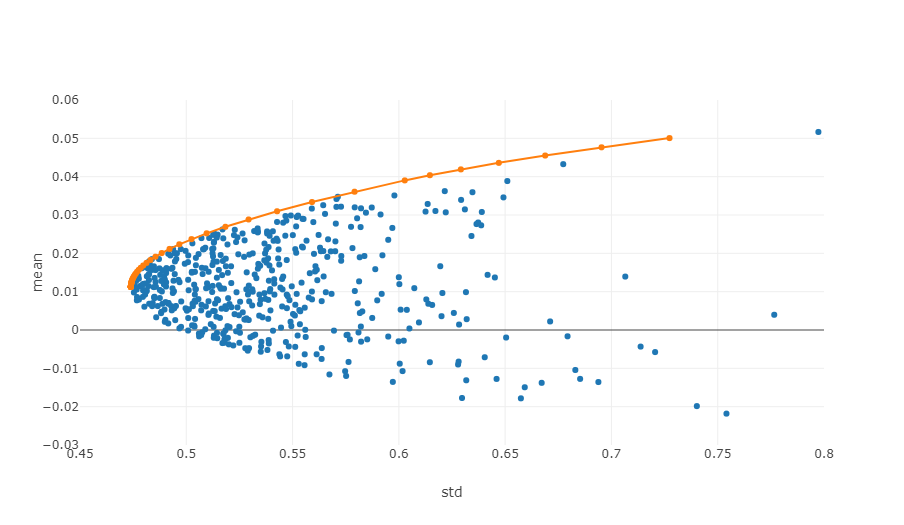
Рисунок выше представляет собой схематическую диаграмму эффективной границы. Каждая точка представляет инвестиционный портфель с различными весами. Горизонтальная ось — это волатильность, то есть уровень риска, а вертикальная ось — норма прибыли. Очевидно, мы ориентируемся на верхнюю границу графика, которая обеспечивает наибольшую доходность при том же уровне риска.
В количественной торговле и управлении портфелем применение этих принципов требует статистического анализа исторических данных и использования математических моделей для оценки ожидаемой доходности, стандартных отклонений и ковариаций различных активов. Затем применяются методы оптимизации для поиска наилучшей конфигурации веса активов. Этот процесс обычно включает в себя сложные математические вычисления и большой объем компьютерной обработки, поэтому количественный анализ стал очень важным в современных финансах. Далее будет использован конкретный пример Python для иллюстрации оптимизации.
Пример кода Python для поиска оптимальной комбинации с использованием метода моделирования
Расчет оптимального портфеля Марковица — многоэтапный процесс, включающий несколько ключевых шагов, таких как подготовка данных, моделирование портфеля и расчет индикаторов. Ссылка: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/
Получить рыночные данные:
- проходить
get_dataФункция получения исторических данных о ценах выбранной цифровой валюты. Это данные, необходимые для расчета нормы доходности и риска, которые используются для построения портфелей и расчета коэффициента Шарпа.
- проходить
Расчет доходности и риска:
- использовать
calculate_returns_riskФункция рассчитывает годовую норму доходности и годовой риск (стандартное отклонение) для каждой цифровой валюты. Это делается для количественной оценки исторической эффективности каждого актива для использования в оптимальном портфеле.
- использовать
Рассчитайте оптимальный портфель Марковица:
- использовать
calculate_optimal_portfolioФункция, моделирующая несколько портфелей. В каждой симуляции веса активов генерируются случайным образом, а затем на основе этих весов рассчитываются ожидаемая доходность и риск портфеля. - Путем случайной генерации комбинаций с разным весом можно исследовать несколько возможных портфелей и найти наилучшую комбинацию. Это одна из основных идей портфельной теории Марковица.
- использовать
Целью всего процесса является поиск портфеля, который обеспечивает наилучшую ожидаемую доходность при заданном уровне риска. Моделируя несколько возможных комбинаций, инвесторы могут лучше понять, как будут работать различные конфигурации, и выбрать комбинацию, которая наилучшим образом соответствует их инвестиционным целям и уровню риска. Такой подход помогает оптимизировать инвестиционные решения и сделать инвестиции более эффективными.
import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt
# 获取行情数据
def get_data(symbols):
data = []
for symbol in symbols:
url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
res = requests.get(url)
data.append([float(line[4]) for line in res.json()])
return data
def calculate_returns_risk(data):
returns = []
risks = []
for d in data:
daily_returns = np.diff(d) / d[:-1]
annualized_return = np.mean(daily_returns) * 365
annualized_volatility = np.std(daily_returns) * np.sqrt(365)
returns.append(annualized_return)
risks.append(annualized_volatility)
return np.array(returns), np.array(risks)
# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
n_assets = len(returns)
num_portfolios = 3000
results = np.zeros((4, num_portfolios), dtype=object)
for i in range(num_portfolios):
weights = np.random.random(n_assets)
weights /= np.sum(weights)
portfolio_return = np.sum(returns * weights)
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))
results[0, i] = portfolio_return
results[1, i] = portfolio_risk
results[2, i] = portfolio_return / portfolio_risk
results[3, i] = list(weights) # 将权重转换为列表
return results
symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)
returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)
max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]
# 输出结果
print("最优组合:")
for i in range(len(symbols)):
print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")
print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")
# 可视化投资组合
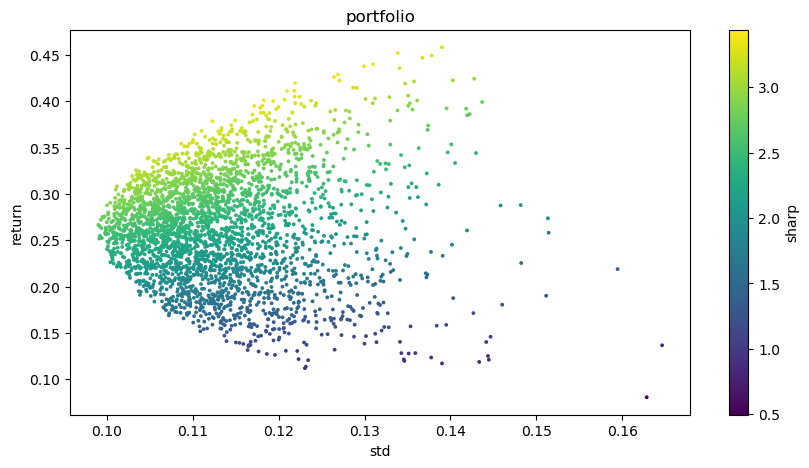
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()
Окончательный результат:
Лучшая комбинация:
BTCUSDT вес: 0.0721
Вес ETHUSDT: 0,2704
BNBUSDT вес: 0.3646
Вес LINKUSDT: 0,1892
BCHUSDT вес: 0.0829
Вес LTCUSDT: 0,0209
Ожидаемая доходность: 0,4195
Ожидаемый риск (стандартное отклонение): 0,1219
Коэффициент Шарпа: 3,4403