Измерение риска и прибыли - введение в теорию Марковица

На прошлой неделе, когда мы представилиКак измерить риск позиции - введение в метод VaR, было упомянуто, что риск портфеля не равен рискам отдельных активов и связан с их ценовой корреляцией. Если взять два актива в качестве примера, если их положительная корреляция очень сильна, то есть они растут и падают вместе, то диверсификация инвестиций не снизит риск. Если есть сильная отрицательная корреляция, диверсифицированные инвестиции могут значительно снизить риск.

Современная теория портфеля (MPT), предложенная Гарри Марковицем в 1952 году, является математической основой для выбора портфеля. Она направлена на максимизацию ожидаемой доходности путем выбора различных комбинаций рисковых активов при одновременном контроле риска.

Ключевое понятие теории Марковица

1. Ожидаемый уровень доходности: Это доходность, которую инвесторы ожидают получить от владения активами или инвестиционного портфеля, как правило, прогнозируемая на основе исторических данных доходности.

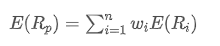
Где?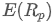ожидаемая доходность портфеля;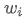- вес i-го актива в портфеле,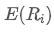представляет собой ожидаемую доходность i-го актива.

2. Риск (волатильность или стандартное отклонение): используется для измерения неопределенности доходности инвестиций или волатильности инвестиций.

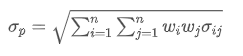
Где?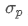представляет собой общий риск портфеля,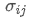Ковариантность актива i и актива j, которая измеряет взаимосвязь между изменением цены этих двух активов.

3. Ковариантность: измеряет взаимную связь между изменениями цен двух активов.

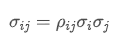
Где?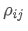является коэффициентом корреляции активов i и j,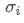и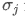являются соответственно стандартными отклонениями актива i и актива j.

4. Эффективная граница: В системе координации риск-доходность эффективной границей является совокупность инвестиционных портфелей, которые могут обеспечить максимальную ожидаемую доходность при заданном уровне риска.

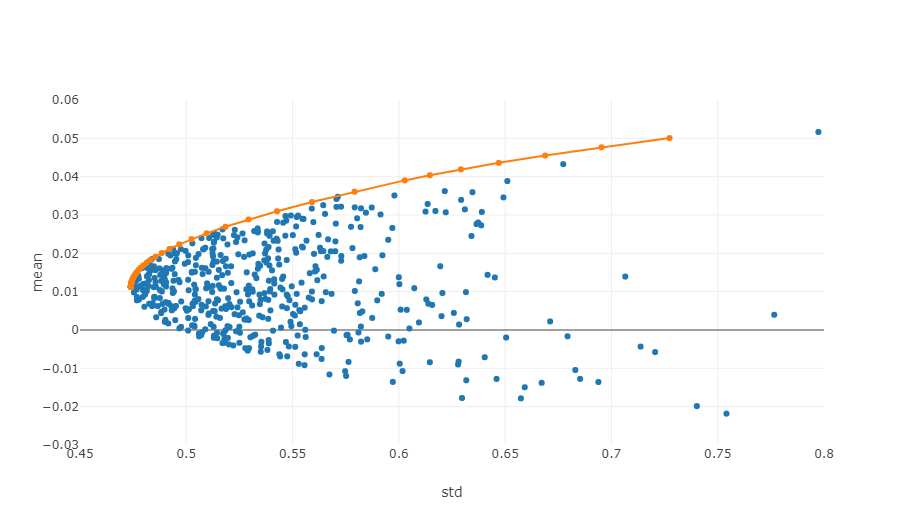
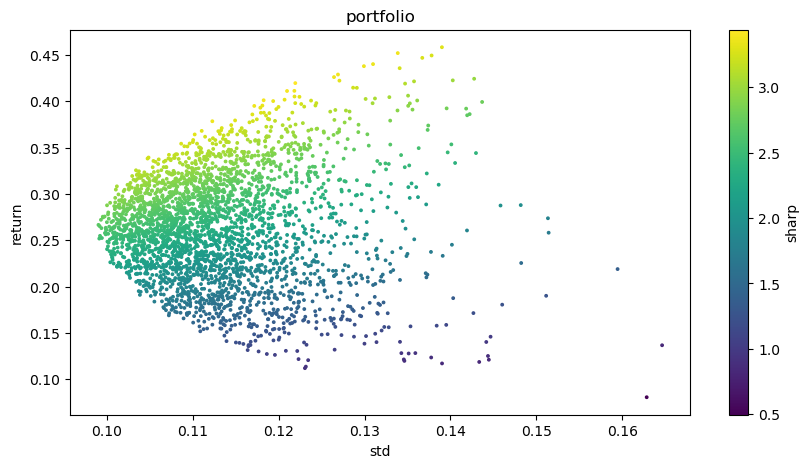
Диаграмма выше представляет собой иллюстрацию эффективной границы, где каждая точка представляет собой различный взвешенный инвестиционный портфель. Ось х обозначает волатильность, которая эквивалентна уровню риска, в то время как ось y означает уровень доходности.

В количественной торговле и управлении портфелем применение этих принципов требует статистического анализа исторических данных и использования математических моделей для оценки ожидаемой доходности, стандартных отклонений и ковариантности для различных активов. Затем используются методы оптимизации для поиска наилучшего распределения веса активов. Этот процесс часто включает в себя сложные математические операции и обширную компьютерную обработку - именно поэтому количественный анализ стал таким важным в современных финансах. Далее мы покажем, как оптимизировать с помощью конкретных примеров Python.

Пример кода Python для поиска оптимальной комбинации с использованием метода моделирования

Расчет оптимального портфеля Марковица - это многоэтапный процесс, включающий несколько ключевых шагов, таких как подготовка данных, моделирование портфеля и расчет показателей.https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Получение данных о рынке:

Черезget_dataЭто необходимые данные для расчета доходности и рисков, которые используются для создания инвестиционных портфелей и расчета коэффициентов Шарпа.

2. Расчет доходности и риска:

Вcalculate_returns_riskЭта функция была использована для вычисления годовой доходности и годового риска (стандартного отклонения) для каждой цифровой валюты.

3. Вычислить оптимальный портфель Марковица:

Вcalculate_optimal_portfolioВ каждом моделировании были произвольно сгенерированы веса активов, а затем на основе этих веса были рассчитаны ожидаемая доходность и риск портфеля. Благодаря случайным комбинациям с различными весами можно исследовать несколько потенциальных инвестиционных портфелей, чтобы найти оптимальный.

Цель всего процесса - найти инвестиционный портфель, который дает наилучшую ожидаемую доходность при заданном уровне риска. Симулируя несколько возможных комбинаций, инвесторы могут лучше понять производительность различных конфигураций и выбрать комбинацию, которая лучше всего соответствует их инвестиционным целям и толерантности к риску. Этот метод помогает оптимизировать инвестиционные решения, делая инвестиции более эффективными.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# Obtain market data
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# Calculate Markowitz Optimal Portfolio
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # Convert weights to a list

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# Output results
print("Optimal combination:")
for i in range(len(symbols)):
    print(f"{symbols[i]} Weight: {optimal_weights[i]:.4f}")

print(f"Expected return rate: {optimal_return:.4f}")
print(f"Expected risk (standard deviation): {optimal_risk:.4f}")
print(f"Sharpe ratio: {optimal_return / optimal_risk:.4f}")

# Visualized investment portfolio
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Конечный результат выхода: Оптимальная комбинация: Вес BTCUSDT: 0,0721 Вес ETHUSDT: 0,2704 Вес BNBUSDT: 0,3646 Вес LINKUSDT: 0,1892 Вес BCHUSDT: 0,0829 Удельный вес LTCUSDT: 0,0209 Ожидаемый уровень доходности: 0,4195 Ожидаемый риск (стандартное отклонение): 0,1219 Соотношение Шарпа: 3,4403