Бэйес - раскрытие тайны вероятности, исследование математической мудрости, лежащей в основе принятия решений

Байесовская статистика является мощной дисциплиной в области математики, с широкими применениями во многих областях, включая финансы, медицинские исследования и информационные технологии.

В этой статье мы кратко познакомимся с некоторыми из главных математиков, основателей этой области.

До Байеса Чтобы лучше понять байесовскую статистику, нам нужно вернуться в 18 век и обратиться к математику Де Моивре и его статье "Доктрина шансов".

В своей статье Де Мойвр решил многие проблемы, связанные с вероятностью и азартными играми в его эпоху.

Один из самых простых вопросов в его статье был:

Какова вероятность того, что вы получите три головы, если трижды подряд подбросить честную монету?

Читая проблемы, описанные в "Доктрине шансов", вы можете заметить, что большинство начинается с предположения, из которого они рассчитывают вероятность для данных событий.

Сегодня это можно выразить в математических терминах так:

Формула

𝑃(𝑋|𝜃)

Но что, если мы не знаем, справедлива ли монета?𝜃 ?

Томас Бэйз и Ричард Прайс

Почти пятьдесят лет спустя, в 1763 году, статья под названием "Решение проблем в доктрине шансов" была опубликована в Philosophical Transactions of the Royal Society of London.

На первых нескольких страницах этого документа есть статья, написанная математиком Ричардом Прайсом, которая обобщает статью, написанную его другом Томасом Бэйзом за несколько лет до его смерти.

На самом деле, он упомянул одну конкретную проблему:

Учитывая количество успехов и неудач неизвестного события, найдите его вероятность между любыми двумя названными степенями.

Другими словами, после наблюдения события мы определяем, какова вероятность того, что неизвестный параметрθЭто одна из первых проблем, связанных со статистическим выводом в истории, и она породила термин обратная вероятность.

Формула

𝑃( 𝜃 | 𝑋）

Это, конечно, то, что мы называем задним распределением теоремы Байеса сегодня.

За причину без причины и следствия

Понимая мотивы исследования этих двух старейшин,Томас БэйзиРичард ПрайсНо чтобы сделать это, нам нужно временно отложить некоторые знания о статистике.

Мы находимся в 18 веке, когда вероятность становится все более интересной областью для математиков. Математики, такие как де Мойвр или Бернулли, уже показали, что некоторые события происходят с определенной степенью случайности, но все еще регулируются фиксированными правилами. Например, если вы бросаете кости несколько раз, одна шестая времени, она попадёт на шесть. Это как будто есть скрытое правило, определяющее шансы судьбы.

Теперь представьте себе, что вы математик и набожный верующий, живущий в этот период.

Они надеялись, что их решение будет непосредственно применимо к доказательству того, что мир должен быть результатом мудрости и интеллекта; следовательно, предоставляя доказательства существования Бога как конечной причины, то есть причины без причинности.

Лаплас

Удивительно, но примерно через два года, в 1774 году, не прочитав работы Томаса Байеса, французский математик Лаплас написал работу под названием "О причинах событий вероятностью событий", которая посвящена проблемам обратной вероятности.

Если событие может быть вызвано n различными причинами, то соотношение между этими причинами вероятности, данные событию, равны вероятностям событий, данным этими причинами; и вероятность существования каждой причины равна вероятности причин, данной этому событию, разделенной на общую вероятность событий, данной каждой из этих причин.

Это то, что мы знаем сегодня как теорема Байеса:

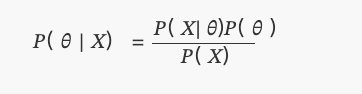
Где?P(θ)равномерное распределение.

Эксперимент с монетами

Мы приведем байесовскую статистику в настоящее время, используя библиотеку Python и PyMC, и проведем простой эксперимент.

Предположим, что друг дает вам монету и спрашивает, считаете ли вы, что это справедливая монета. Поскольку он спешит, он говорит вам, что вы можете бросить монету только 10 раз. Как вы можете видеть, есть неизвестный параметрpв этой задаче, которая является вероятностью получения головы в бросании монет, и мы хотим оценить наиболее вероятное значениеp.

(Примечание: мы не говорим, что параметрpявляется случайной переменной, но скорее, что этот параметр фиксирован; мы хотим знать, где это наиболее вероятно между.)

Чтобы иметь разные взгляды на эту проблему, мы решим ее под двумя различными предварительными убеждениями:

• 1. У вас нет предварительной информации о справедливости монеты, поэтому вы присваиваете равную вероятностьpВ этом случае мы будем использовать так называемое неинформативное предварительное, потому что вы не добавили никакой информации к своим убеждениям.
• 2. Из своего опыта вы знаете, что даже если монета может быть несправедливой, трудно сделать ее чрезвычайно несправедливой.pВ этом случае мы будем использовать информативный прериор.

Для этих двух сценариев наши предварительные убеждения будут следующими:

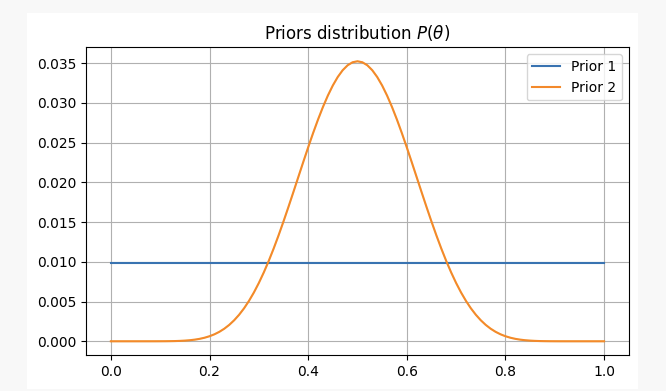
После того, как мы подбросили монету 10 раз, мы получили две головы.p?

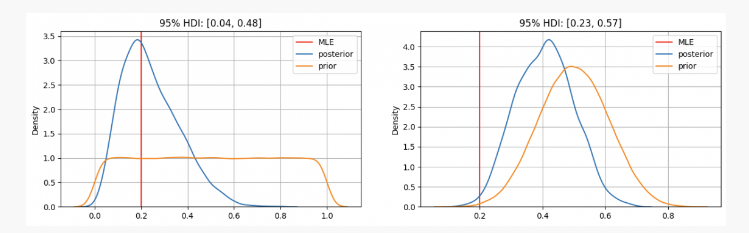
Как вы можете видеть, в первом случае, наше предварительное распределение параметраpсосредоточена на максимальной вероятности оценки (MLE)p=0.2, который является методом, аналогичным тому, который используется школой частот.

С другой стороны, в случаях, когда есть высокая уверенность, что параметрpВ этом случае истинный неизвестный параметр будет находиться в пределах 95% доверительного интервала между 0,23 и 0,57.

Поэтому в первом случае вы с уверенностью скажете своему другу, что эта монета не справедлива, но в другом случае вы скажете, что вы не уверены, справедлива она или нет.

Как вы можете видеть, даже когда мы сталкиваемся с идентичными доказательствами (две головы из десяти бросков), при различных предыдущих убеждениях результаты могут сильно варьироваться; одно преимущество байесовской статистики над традиционными методами заключается здесь: как и научная методология, она позволяет нам обновлять наши убеждения, объединяя их с новыми наблюдениями и доказательствами.

Окончание

В сегодняшней статье мы рассмотрели происхождение байесовской статистики и ее основных авторов.quantdare.com.