В предыдущей статье (https://www.fmz.com/digest-topic/4187) мы представили стратегии парной торговли и продемонстрировали, как использовать данные и математический анализ для создания и автоматизации торговых стратегий.

Сбалансированная стратегия длинных и коротких позиций на рынке акций является естественным расширением стратегии парной торговли, применимой к корзине торговых целей. Он особенно подходит для торговых рынков со множеством разновидностей и взаимосвязей, таких как рынок цифровых валют и рынок товарных фьючерсов.

Основные принципы

Сбалансированная стратегия длинных и коротких позиций заключается в одновременном открытии длинных и коротких позиций по корзине торговых целей. Как и в парной торговле, определите, какие инвестиционные цели дешевые, а какие дорогие. Разница в том, что стратегия сбалансированного капитала с длинными и короткими позициями сортирует все инвестиционные цели в пул выбора акций, чтобы определить, какие инвестиционные цели относительно дешевые. Или дорогие. Затем он откроет длинную позицию по n верхним инвестициям в соответствии с рейтингом и короткую позицию по n нижним инвестициям на равную сумму (общая стоимость длинных позиций = общей стоимости коротких позиций).

Помните, мы говорили ранее, что парная торговля — это рыночно-нейтральная стратегия? То же самое справедливо и для сбалансированной стратегии длинных и коротких позиций, поскольку равные объемы длинных и коротких позиций гарантируют, что стратегия останется нейтральной по отношению к рынку (не подверженной колебаниям рынка). Стратегия также статистически надежна: ранжируя инвестиции и занимая несколько позиций, вы можете подвергнуть свою модель ранжирования многократным рискам, а не только единовременному риску. Все, на что вы делаете ставку, — это качество вашей рейтинговой схемы.

Что такое схема ранжирования?

Схема ранжирования — это модель, которая назначает приоритет каждой инвестиционной цели на основе ее ожидаемой эффективности. Факторами могут быть факторы стоимости, технические индикаторы, модели ценообразования или комбинация всего вышеперечисленного. Например, вы можете использовать показатель импульса для ранжирования списка инвестиций, следующих за трендом: инвестиции с самым высоким импульсом, как ожидается, продолжат демонстрировать хорошие результаты и получат самые высокие рейтинги; инвестиции с самым низким импульсом будут демонстрировать наихудшие результаты и имеют самую низкую доходность.

Успех этой стратегии почти полностью зависит от используемой схемы ранжирования, то есть ваша схема ранжирования способна отделить высокоэффективные инвестиции от низкоэффективных инвестиций, лучше реализуя доходность целевой стратегии долгосрочных и краткосрочных инвестиций. Поэтому очень важно разработать схему ранжирования.

Как составить план ранжирования?

Как только у нас появится схема ранжирования, мы, очевидно, захотим извлечь из нее прибыль. Мы делаем это, вкладывая одинаковую сумму денег в длинные позиции по инвестициям с самым высоким рейтингом и короткие позиции по инвестициям с самым низким рейтингом. Это гарантирует, что стратегия будет зарабатывать деньги только пропорционально качеству ее рейтингов и будет «нейтральной по отношению к рынку».

Предположим, вы ранжируете все инвестиции m, имеете n долларов для инвестирования и хотите занять в общей сложности 2p (где m>2p) позиций. Если ожидается, что инвестиции с рангом 1 покажут наихудшие результаты, то ожидается, что инвестиции с рангом m покажут наилучшие результаты:

• Вы расставляете инвестиционные цели следующим образом: 1, …, p и короткие инвестиционные цели 2/2p USD

• Вы расставляете инвестиционные цели следующим образом: m-p,……,m, и открываете длинную позицию на n/2p долларов инвестиционных целей.

Уведомление:Поскольку цена инвестиционной цели из-за скачков цен не всегда будет делить n/2p поровну, а некоторые инвестиционные цели должны приобретаться целыми числами, будут некоторые неточные алгоритмы, и алгоритм должен быть максимально приближен к этому числу. Для запуска стратегии с n = 100000 и p = 500 мы видим:

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

Это может вызвать большие проблемы для цен с дробными значениями больше 100 (например, на рынках товарных фьючерсов), поскольку вы не можете открывать позиции с дробными значениями цен (на рынке криптовалют такой проблемы не существует). Мы смягчаем это за счет сокращения сделок с дробной ценой или увеличения капитала.

Давайте рассмотрим гипотетический пример.

• Создание нашей исследовательской среды на платформе Inventor Quantitative

Прежде всего, чтобы работать гладко, нам нужно построить нашу исследовательскую среду. В этой статье мы используем Inventor Quantitative Platform (FMZ.COM) для построения исследовательской среды, в основном для того, чтобы мы могли использовать удобный и быстрый API Интерфейс и инкапсуляция этой платформы позже. Полная система Docker.

В официальном названии Inventor Quantitative Platform эта система Docker называется хост-системой.

Более подробную информацию о том, как развертывать хосты и роботов, можно найти в моей предыдущей статье: https://www.fmz.com/bbs-topic/4140

Читатели, желающие приобрести собственный хост для развертывания сервера облачных вычислений, могут обратиться к этой статье: https://www.fmz.com/bbs-topic/2848

После успешного развертывания сервиса облачных вычислений и хост-системы мы установим самый мощный инструмент Python: Anaconda.

Чтобы реализовать все необходимые для этой статьи программные среды (зависимые библиотеки, управление версиями и т. д.), проще всего использовать Anaconda. Это пакетная экосистема Python для обработки и анализа данных, а также менеджер зависимостей.

Информацию о способе установки Anaconda см. в официальном руководстве Anaconda: https://www.anaconda.com/distribution/

В этой статье также будут использоваться numpy и pandas — две очень популярные и важные библиотеки в научных вычислениях на Python.

Для вышеприведенной базовой работы вы также можете обратиться к моей предыдущей статье, в которой рассказывается, как настроить среду Anaconda и две библиотеки numpy и pandas. Подробности см.: https://www.fmz.com/digest- тема/4169

Мы генерируем случайные инвестиции и случайные факторы и ранжируем их. Предположим, что наши будущие доходы фактически зависят от значений этих факторов.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

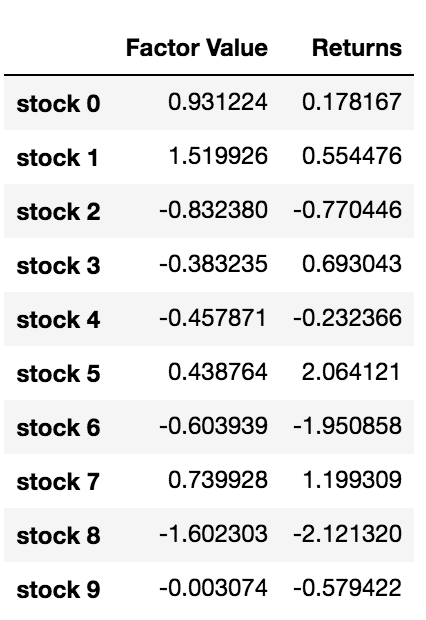
Теперь, когда у нас есть значения факторов и доходности, мы можем увидеть, что произойдет, если мы ранжируем инвестиции на основе значений факторов, а затем откроем длинные и короткие позиции.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

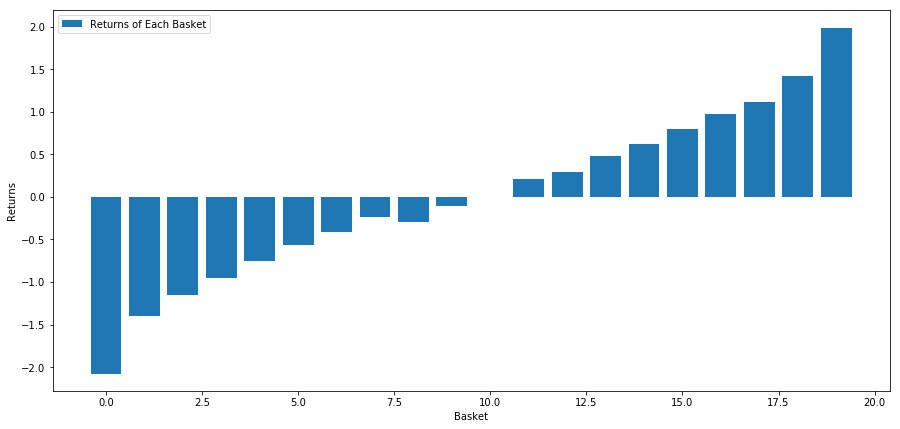
Наша стратегия заключается в том, чтобы занять длинную позицию по первой по рангу инвестиционной цели в корзине инвестиционных целей и короткую позицию по десятой по рангу инвестиционной цели. Преимущества этой стратегии:

basket_returns[number_of_baskets-1] - basket_returns[0]

Результат: 4.172

Вложите свои деньги в нашу модель ранжирования, чтобы отделить высокоэффективные инвестиции от малоэффективных.

В оставшейся части статьи мы обсудим, как оценивать схемы ранжирования. Преимущество зарабатывания денег на арбитраже на основе рейтинга заключается в том, что он не подвержен влиянию рыночного хаоса, а наоборот, может извлечь из него выгоду.

Давайте рассмотрим реальный пример.

Мы загружаем данные по 32 акциям из разных секторов индекса S&P 500 и пытаемся ранжировать их.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Давайте используем нормализованный индикатор импульса за месячный период в качестве основы для ранжирования.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Теперь мы проанализируем поведение наших акций и посмотрим, как они ведут себя на рынке с учетом выбранных нами факторов ранжирования.

Анализ данных

Поведение акций

Давайте посмотрим, как выбранная нами корзина акций ведет себя в нашей модели рейтинга. Для этого давайте рассчитаем недельную форвардную доходность для всех акций. Затем мы можем рассмотреть корреляцию 1-недельной форвардной доходности каждой акции с предыдущим 30-дневным импульсом. Акции, которые показывают положительную корреляцию, следуют за трендом, а акции, которые показывают отрицательную корреляцию, возвращаются к среднему значению.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

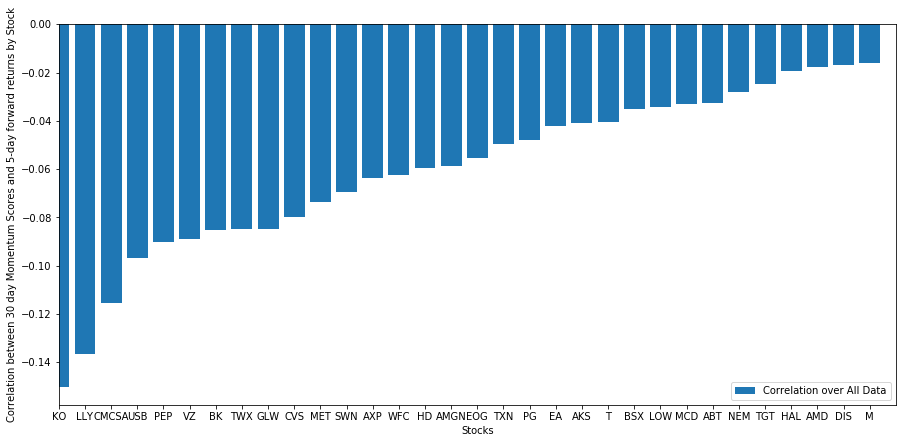
Все наши акции в той или иной степени подразумевают возврат! (По-видимому, выбранная нами вселенная работает именно так) Это говорит нам о том, что если акция имеет высокий рейтинг в анализе импульса, мы должны ожидать, что на следующей неделе она покажет худшие результаты.

Корреляция между рейтингом Momentum Score и доходностью

Далее нам нужно рассмотреть корреляцию между нашим рейтинговым баллом и общей форвардной доходностью рынка, то есть связь между прогнозом ожидаемой доходности и нашими факторами ранжирования. Могут ли более высокие уровни корреляции предсказать худшую относительную доходность или наоборот?

Для этого мы рассчитываем дневную корреляцию между 30-дневным импульсом и 1-недельной форвардной доходностью для всех акций.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

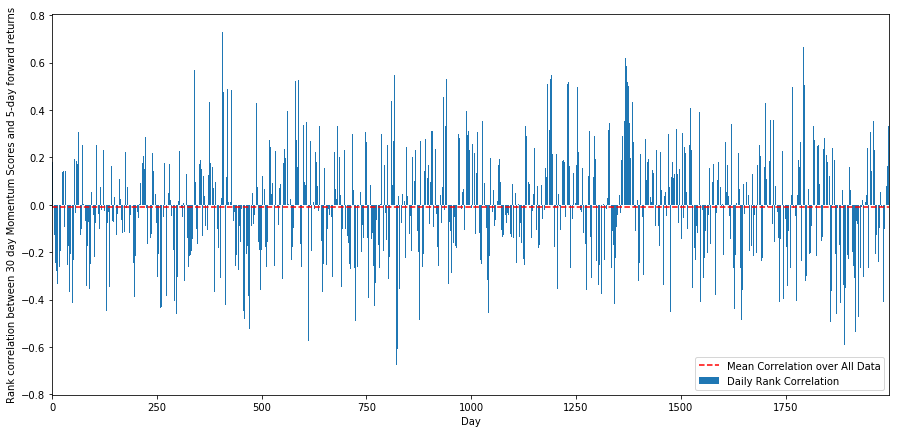
Дневная корреляция довольно шумная, но очень слабая (что и ожидалось, поскольку мы говорили, что все акции будут означать возврат). Мы также рассматриваем среднюю месячную корреляцию форвардной доходности за 1 месяц.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

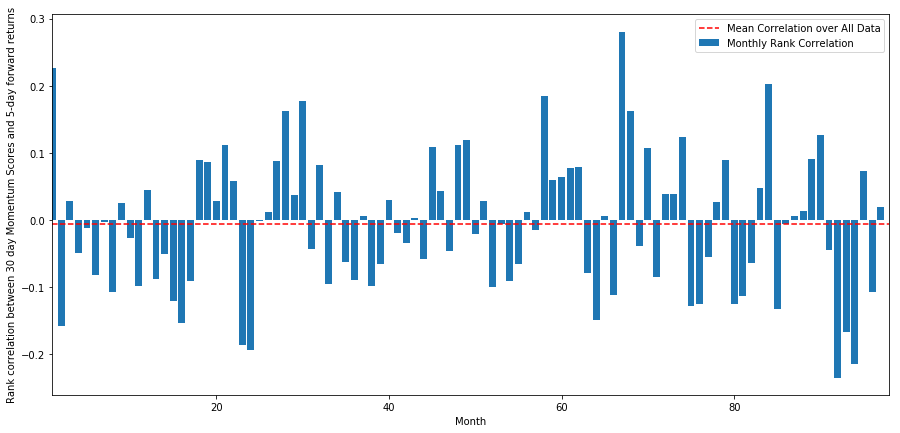
Мы видим, что средняя корреляция снова слегка отрицательная, но также сильно варьируется от месяца к месяцу.

Средняя доходность корзины акций

Мы рассчитали доходность корзины акций, взятых из нашего рейтинга. Если мы ранжируем все акции, а затем разделим их на n групп, какова будет средняя доходность каждой группы?

Первым шагом является создание функции, которая будет выдавать среднюю доходность и фактор ранжирования для каждой корзины за каждый месяц.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

При ранжировании акций на основе этого показателя мы рассчитываем среднюю доходность для каждой корзины. Это должно дать нам хорошее представление об их отношениях на протяжении длительного периода времени.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

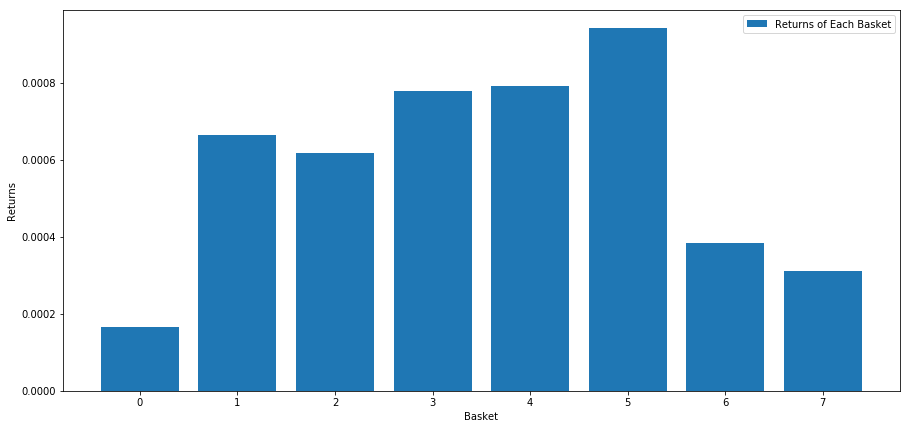
Похоже, нам удается отделить успешных от неудачных.

Консистенция спреда (базы)

Конечно, это всего лишь среднестатистические отношения. Чтобы понять, насколько последовательны отношения и готовы ли мы заключить сделку, нам следует со временем менять свой подход и отношение к ним. Далее мы рассмотрим их месячные спреды (базис) за предыдущие два года. Мы можем увидеть больше изменений и провести дополнительный анализ, чтобы определить, является ли этот показатель импульса пригодным для торговли.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

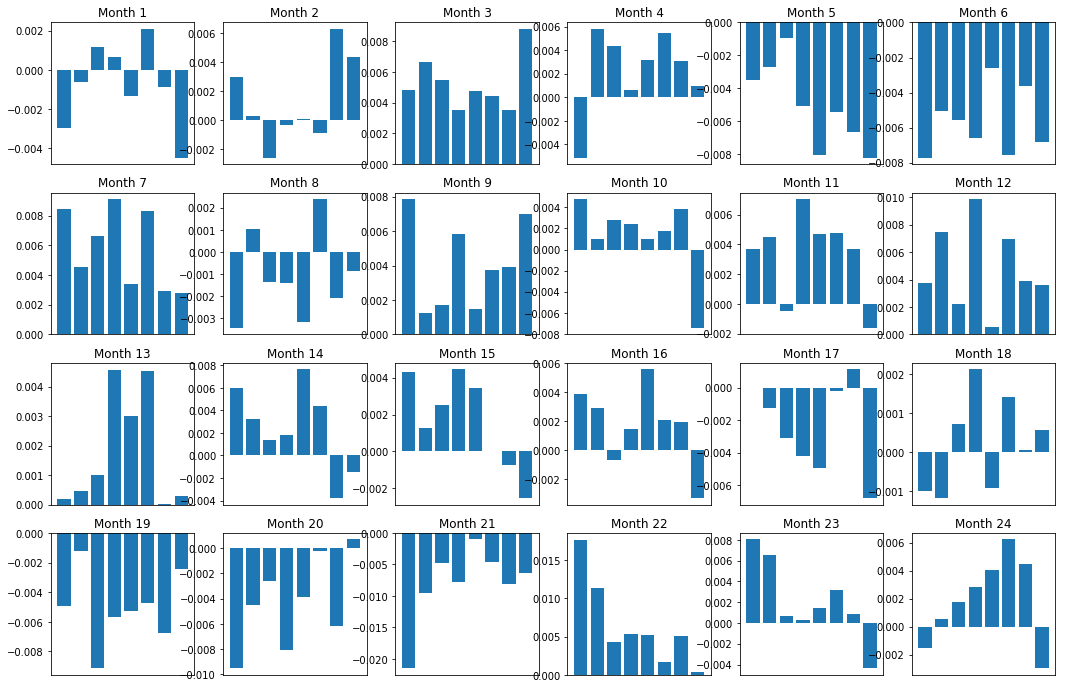
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

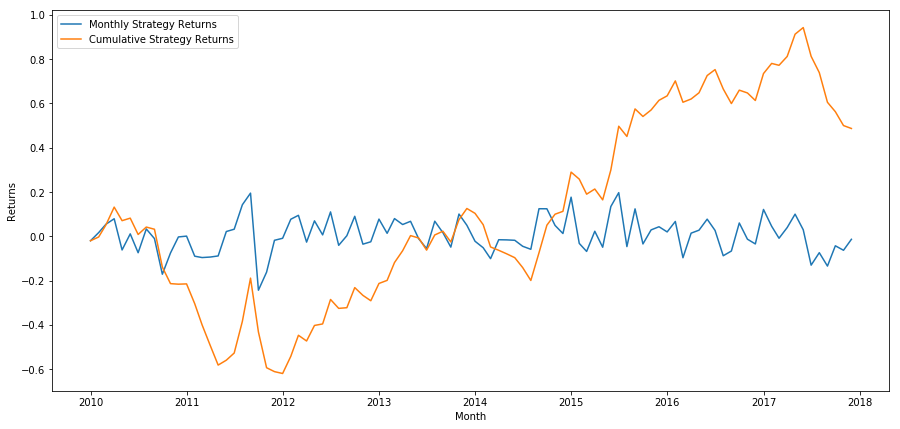
Наконец, давайте посмотрим на доходность, если бы мы открывали длинную позицию по последней корзине и короткую позицию по первой корзине каждый месяц (предполагая равное распределение капитала по каждой ценной бумаге).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Годовая доходность: 5,03%

Мы видим, что у нас очень слабая схема ранжирования, которая лишь скромно отличает высокоэффективные акции от низкоэффективных. Кроме того, в этой схеме рейтинга нет единообразия, и она существенно меняется от месяца к месяцу.

Поиск правильной схемы ранжирования

Чтобы реализовать сбалансированную стратегию длинно-коротких позиций, вам на самом деле нужно только определить схему ранжирования. Все, что происходит после этого, — механическое. Как только у вас появится сбалансированная стратегия по длинным и коротким позициям, вы сможете менять местами различные факторы ранжирования, не меняя ничего больше. Это очень удобный способ быстрой реализации ваших идей, не беспокоясь о необходимости каждый раз вносить изменения в весь код.

Схему ранжирования можно взять практически из любой модели. Это не обязательно должна быть факторная модель, основанная на стоимости, это может быть метод машинного обучения, который прогнозирует доходность на месяц вперед и ранжирует ее на основе этого.

Выбор и оценка схем ранжирования

Схема ранжирования является преимуществом стратегии сбалансированного капитала с длинными и короткими позициями, а также ее наиболее важным компонентом. Выбор хорошей схемы ранжирования — это систематический проект, и простых ответов здесь нет.

Хорошей отправной точкой будет выбор существующих известных технологий и попытка их незначительной модификации для получения более высокой отдачи. Здесь мы обсудим несколько отправных точек:

• Клонировать и настроить: Выберите что-то, что часто обсуждается, и посмотрите, сможете ли вы немного изменить это в свою пользу. Как правило, публичные факторы больше не будут иметь торговых сигналов, поскольку они были полностью выведены с рынка путем арбитража. Однако иногда они могут направить вас в правильном направлении.

• Модель ценообразования: Любая модель, прогнозирующая будущую доходность, может быть фактором и потенциально может использоваться для ранжирования вашей корзины торговых целей. Вы можете взять любую сложную модель ценообразования и преобразовать ее в схему ранжирования.

• Факторы, основанные на цене (технические индикаторы): Факторы, основанные на цене, подобные тем, которые мы обсуждали сегодня, берут информацию об исторической цене каждой акции и используют ее для генерации значения фактора. Примерами могут служить индикаторы скользящей средней, индикаторы импульса или индикаторы волатильности.

• Регресс и импульс: Стоит отметить, что некоторые факторы полагают, что если цены движутся в одном направлении, то они продолжат двигаться в этом направлении. Некоторые факторы прямо противоположны. Обе модели являются действительными для разных временных интервалов и активов, и важно изучить, основано ли базовое поведение на импульсе или регрессии.

• Фундаментальные факторы (основанные на ценности): Здесь используется комбинация фундаментальных значений, таких как P/E, дивиденды и т. д. Фундаментальная стоимость содержит информацию, связанную с реальными фактами о компании, и поэтому может быть более значимой, чем цена, во многих отношениях.

В конечном итоге разработка предсказателей — это гонка вооружений, в которой вы пытаетесь быть на шаг впереди. Факторы являются предметом арбитража на рынке и имеют определенный срок службы, поэтому вам необходимо постоянно работать над тем, чтобы определить, насколько сильно обесценились ваши факторы и какие новые факторы можно использовать для их замены.

Другие соображения

• Частота ребалансировки

Каждая рейтинговая система прогнозирует доходность за несколько разный период времени. Возврат к среднему значению на основе цены может быть прогнозным на период в несколько дней, в то время как факторные модели на основе стоимости могут быть прогнозными на период в несколько месяцев. Очень важно определить временной горизонт, который должна прогнозировать модель, и подтвердить его статистически, прежде чем приступать к реализации стратегии. Вы определенно не хотите переобучать, пытаясь оптимизировать частоту ребалансировки; вы неизбежно найдете тот, который случайным образом превзойдет другие. Как только вы определили временной горизонт, который предсказывает ваша схема ранжирования, попробуйте ребалансировать примерно с этой частотой, чтобы Получите максимальную отдачу от своей модели.

• Капиталовложение и транзакционные издержки

Каждая стратегия имеет минимальные и максимальные требования к капиталу, при этом минимальный порог обычно определяется транзакционными издержками.

Торговля слишком большим количеством акций приведет к высоким транзакционным издержкам. Предположим, вы хотите купить 1000 акций, каждая ребалансировка потребует затрат в несколько тысяч долларов. Ваша капитальная база должна быть достаточно высокой, чтобы транзакционные издержки составляли лишь небольшую часть прибыли, получаемой от вашей стратегии. Например, если ваш капитал составляет 100 000 долларов США, а ваша стратегия приносит 1% (1000 долларов США) в месяц, то весь этот доход будет съеден транзакционными издержками. Для реализации этой стратегии и получения прибыли от более чем 1000 акций вам понадобятся миллионы долларов капитала.

Минимальный порог активов зависит в основном от количества торгуемых акций. Однако максимальная емкость также очень высока, и сбалансированные стратегии длинных и коротких позиций на рынке акций позволяют торговать сотнями миллионов долларов, не теряя при этом своего преимущества. Это верно, потому что стратегия перебалансируется относительно редко. Общая сумма активов, деленная на количество торгуемых акций, даст очень низкую стоимость в долларах за акцию, и вам не придется беспокоиться о том, что ваш торговый объем будет двигать рынок. Допустим, вы торгуете 1000 акций, это 100 000 000 долларов. Если бы вы ежемесячно ребалансировали весь свой портфель, вы бы торговали акциями на сумму всего 100 000 долларов в месяц, что недостаточно для того, чтобы занять значительную долю рынка для большинства ценных бумаг.