Сортировка FMEX обеспечивает оптимальную оптимизацию количества заказов
 0
0
 2180
2180

Крах FMEX доставил массу неприятностей многим людям, но недавно компания разработала план перезапуска и сформулировала правила, аналогичные правилам первоначального майнинга, чтобы разблокировать долги. Была представлена аналитическая статья по майнингу транзакций: https://www.fmz.com/bbs-topic/5834. Также имеются возможности для оптимизации сортировочной добычи. Хотя люди не должны дважды попадать в одну и ту же яму, те, у кого есть претензии к FMEX, могут пожелать обратиться к ней. Также могут быть опубликованы конкретные стратегии в реальном времени, которые можно будет запустить на количественной платформе FMZ.
Правила разблокировки сортировки FMEX
Определим каждые 5 минут каждого дня как цикл разблокировки сортировки, и каждому циклу будет выделена 1⁄288 квоты разблокировки сортировки пары транзакций в этот день. В каждом цикле выбирается случайный момент времени, чтобы сделать снимок ордеров на покупку и продажу торговой пары, где:
- Купить 1 На основе пропорции суммы заказа пользователя, 1⁄4 суммы возврата периода разблокировки выделяется на этот рейтинг
- Продажа 1 Согласно пропорции суммы заказа пользователя, 1⁄4 суммы возврата периода разблокировки выделяется на этот рейтинг
- Для 4 уровней от покупки 2 до покупки 5 на каждый уровень будет выделена 1⁄40 суммы возврата за период разблокировки в соответствии с долей суммы заказа пользователя на каждом уровне.
- Для заказов на 4 уровнях от продажи 2 до продажи 5 будет выделена 1⁄40 суммы возврата за период разблокировки рейтинга в соответствии с долей суммы заказа пользователя на каждом уровне.
- Для пяти заказов от Buy 6 до Buy 10 на каждый заказ будет выделена 1⁄50 суммы возврата за период разблокировки в соответствии с пропорцией суммы заказа в каждом заказе.
- Для пяти уровней ордеров на продажу с 6 по 10 на каждый уровень будет выделена 1⁄50 суммы возврата за период разблокировки в соответствии с долей суммы ордера пользователя на каждом уровне.
- Для пяти заказов от Buy 11 до Buy 15 на каждый заказ будет выделена 1⁄100 суммы возврата за период разблокировки в соответствии с пропорцией суммы заказа в каждом заказе.
- Для пяти ордеров от Sell 11 до Sell 15 на каждый ордер будет выделена 1⁄100 суммы возврата за период разблокировки в соответствии с пропорцией суммы ордера в каждом ордере.
Общий доход от разблокировки рейтинга пользователя в определенной торговой паре в один и тот же день представляет собой сумму сумм, возвращенных пользователю за разблокировку рейтинга в каждом цикле торговой пары.
Сортировка для разблокировки преимуществ
Во-первых, общий доход от сортировки и разблокировки составляет:
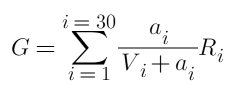
Здесь i представляет одну из позиций, всего позиций для обеих сторон 30, a — объем отложенного ордера, R — сумма разблокируемого возврата, а V — общее количество существующих ордеров.
В отличие от разблокировки транзакции, размещение заказа не имеет стоимости. Здесь R нужно учитывать только относительный размер, и нет необходимости учитывать абсолютную сумму, выраженную в USDT. Если мы определим общее количество отложенных ордеров, то встанет вопрос, как распределить ордера по разным позициям, чтобы максимизировать прибыль G. Очевидно, что простой поиск местоположения с наименьшим объемом заказов и размещение всех заказов там не является оптимальным решением. Например, есть три позиции с 10 существующими ордерами, и их R одинаковый. Мы устанавливаем общий объем ордера 30. Если мы выберем только одну позицию для размещения ордера, окончательная общая прибыль составит 0,75R. 10, Конечная прибыль составляет 1,5R, что показывает, что иногда прибыль от рассредоточенных ордеров выше. Так как же распределить средства?
Оптимизация сортировки разблокировки
Наконец, наши цели и ограничения оптимизации таковы:
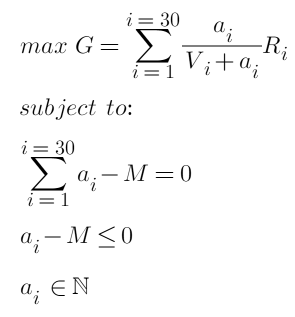
Где M — общий объем заказа. Это задача квадратичной выпуклой оптимизации с неравенствами, которая удовлетворяет условию KTT и имеет целочисленное решение. Используя соответствующий пакет и решатель выпуклой оптимизации, можно будет напрямую получить результаты и вернуть оптимальный объем заказа для каждой позиции. Но это явно не тот ответ, который нам нужен. Нам нужно упростить задачу и получить конкретные шаги решения.
Давайте начнем с простого примера.
Рассмотрим только два уровня. Текущие суммы заказов составляют 10 и 20 (называемые первым и вторым уровнями соответственно). Их квоты разблокировки составляют R. Общее количество стратегических заказов составляет 30. Как их следует распределить? максимально увеличена ли разблокированная сумма средств? Этот вопрос кажется простым, но трудно сделать правильный вывод без расчета. Читатели могут сначала подумать об ответе сами.
Сценарий 1:
Найдите минимальную позицию ордера и разместите все ордера там, общая прибыль G=30/(30+10)=0,75R. Это также самое простое решение, которое можно придумать.
Сценарий 2:
Каждый раз выделяется 1 юань и направляется в то место, которое может принести наибольшую прибыль, то есть в место с наименьшим количеством отложенных ордеров. Затем первый юань будет выделен на первый уровень, а объем заказа первого уровня станет 10+1. Второй юань также будет выделен на первый уровень… и так далее, пока общая сумма не составит 10 юаней. распределяется на первый уровень. В это время один будет выбран случайным образом, и когда общее количество отложенных ордеров на первом уровне превысит 20, он будет распределен на второй уровень. В результате 20 юаней выделяется на первый уровень, а 10 юаней — на второй уровень, а их окончательные заказы составляют 30 юаней. Общая прибыль G=20⁄30+10⁄30=R. Это решение намного лучше решения 1 и его легче рассчитать.
Сценарий 3:
Мы можем предположить, что первый уровень выделен a, а второй уровень - 30-a. Тогда мы можем напрямую перечислить уравнение и найти его производную как 0 (процесс здесь не указан, он похож на статью о разблокировке транзакций ), и вычисляем окончательный результат. Формула:
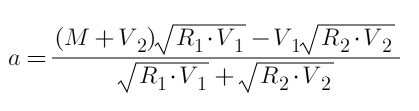
Подставим целое число и получим a=15. Общая прибыль G=15⁄25+15⁄35=1.0286R, что лучше, чем Вариант 2. Поскольку он напрямую выводится из формулы, это оптимальное решение. Читатели могут проверить его.
Результат может отличаться от того, что вы ожидали. Очевидно, что распределение каждого доллара в Плане 2 является оптимальным решением в текущих обстоятельствах. Почему это не является общим оптимальным решением? Такая ситуация очень распространена. Локальный оптимум не обязательно является общим оптимумом, поскольку до распределения заказы уже имеют инвестированные средства, а общая эффективность должна учитывать невозвратные издержки. Наша цель на каждом этапе оптимизации — максимизировать общую эффективность, а не максимизировать отдельное преимущество.
Конкретный план оптимизации
Наконец, мы начали реальную осуществимую операцию. Давайте упростим задачу, выделяя по 1 юаню каждый раз. Сначала давайте измерим эффективность. Производная может отражать вклад каждого a в G. Этот вклад учитывает кумулятивную стоимость, а не выгоду от одного распределения. Чем больше значение, тем больше общий вклад в конечную выгоду . Очевидно, согласно графику функции, при a=1 эффективность максимальна от существования до несуществования, а затем постепенно уменьшается.
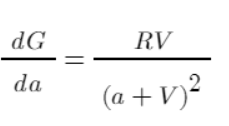
Взяв за основу простой пример, приведенный выше, мы можем рассчитать эффективность распределения средств и перечислить их в таблице:
| фонды | 1 | 2 |
|---|---|---|
| 1 | 0.0826 | 0.0454 |
| 2 | 0.069 | 0.0413 |
| 3 | 0.0592 | 0.0378 |
| 4 | 0.051 | 0.0347 |
| 5 | 0.0444 | 0.032 |
| … | … | … |
|12 | 0.0207 |0.0195| |13 | 0.0189 |0.0184| |14 | 0.0174 |0.0173| |15 | 0.016 |0.0163| |16 | 0.0148 |0.0154| |17 | 0.0137 |0.0146| |18 | 0.0128 |0.0139|
Согласно таблице, первый юань выделяется на первый уровень, второй юань выделяется на первый уровень… пятый юань выделяется на второй уровень… и так далее, и, наконец, 15 юаней выделяются на первый уровень и 15 юаней на второй уровень. Юаней, что является оптимальным решением, которое мы рассчитали на основе уравнения. Конкретно для 30-й передачи алгоритм тот же, а конкретные шаги таковы:
- 1. Сначала проверьте все передачи. Если V=0, то a=1, и больше средства не будут выделены.
- 2. Распределите общие средства на N частей и каждый раз выбирайте механизм распределения.
- 3. Рассчитайте эффективность каждой передачи = RV/pow(a+V,2), где a представляет собой накопленные средства, выделенные на позицию + средства, выделенные на этот раз.
- 4. Выделите средства на наиболее эффективное снаряжение и случайным образом выберите то, эффективность которого одинакова.
- 5. Повторяйте 3-4, пока средства не будут выделены.
Если наш общий объем заказа большой, то слишком неэффективно распределять каждый доллар за раз. Мы можем разделить средства на 100 частей и распределять по одной части за раз. Поскольку это всего лишь простой расчет и сортировка, алгоритм очень эффективный. В частности, на уровне исполнения все еще есть возможности для оптимизации, например, разделения наших заказов на 100, чтобы каждый раз при внесении корректировок нам нужно было только перераспределять заказы, а не отменять их все. Вы также можете самостоятельно установить значение R и придать больший вес тем, которые далеки от рынка. Если есть совпадения между разблокировкой сортировки и разблокировкой отложенного ордера, вы можете рассмотреть их вместе и т. д.
Эта статья является оригинальной статьей FMZ Quantitative Platform. Пожалуйста, укажите источник при переводе: https://www.fmz.com/bbs-topic-new/5843