Моделирование и анализ волатильности биткоина на основе модели ARMA-EGARCH

Недавно я сделал анализ волатильности биткойна, который является словесным и спонтанным. Поэтому я просто делюсь некоторыми моими пониманиями и кодом следующим образом. Мои способности ограничены, и код не очень совершенен. Если есть какая-либо ошибка, пожалуйста, укажите и исправьте ее напрямую.

1. Краткое описание временных рядов финансов

Временные ряды финансов - это набор моделей стохастических процессов, основанных на переменной, наблюдаемой в временном измерении. Переменной обычно является ставка доходности активов. Поскольку ставка доходности независима от масштаба инвестиций и имеет статистический характер, более ценным является анализ инвестиционных возможностей базовых финансовых активов.

Здесь смело предполагается, что уровень доходности Биткоина соответствует характеристикам уровня доходности общих финансовых активов, то есть это слабо гладкий ряд, который можно продемонстрировать путем тестирования согласованности нескольких образцов.

1.1 Препараты, импортируемые библиотеки, функции инкапсулирования

Конфигурация исследовательской среды завершена. Библиотека, необходимая для последующих вычислений, импортируется сюда. Поскольку она записывается периодически, она может быть излишней. Пожалуйста, очистите ее самостоятельно.

В [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

Выход[1]: {Ставка: 10000.0, СмороженнаяСтавка: 0.0, Стоки: 0.0, СмороженныеСтоки: 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

В [17]:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

Давайте начнем с краткого понимания исторических данных Биткоина.

С статистической точки зрения, мы можем взглянуть на некоторые характеристики данных Биткоина. Принимая в качестве примера описание данных за последний год, коэффициент доходности рассчитывается простым способом, то есть цена закрытия вычитается логарифмически. Формула выглядит следующим образом: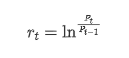

В [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

Выход[3]: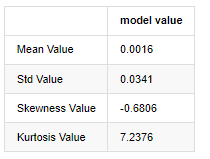

Особенность толстых жирных хвостов заключается в том, что чем короче временная шкала, тем более значительна особенность. Куртоз увеличивается с увеличением частоты передачи данных, и особенность будет очень очевидна в высокочастотных данных.

Взяв в пример ежедневные данные о цене закрытия с 1 января 2019 года по настоящее время, мы проводим описательный анализ его логарифмической нормы доходности, и можно увидеть, что простой ряд нормы доходности Биткоина не соответствует нормальному распределению, и он имеет очевидную характеристику толстых жирных хвостов.

Среднее значение последовательности составляет 0,0016, стандартное отклонение - 0,0341, искаженность - 0,6819, куртоз - 7,2243, что намного выше нормального распределения и имеет характеристику толстых жирных хвостов.

В [4]:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

Выход[4]:

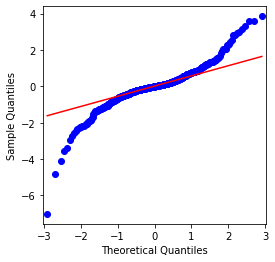
Можно видеть, что QQ-графика идеальна, а логарифмическая серия возврата для Биткоина не соответствует нормальному распределению из результатов, и она имеет явную характеристику толстых жирных хвостов.

Далее рассмотрим эффект агрегации волатильности, то есть финансовые временные ряды часто сопровождаются большей волатильностью после большей волатильности, в то время как меньшая волатильность обычно сопровождается меньшей волатильностью.

Кластеризация волатильности отражает положительные и отрицательные эффекты обратной связи волатильности и сильно коррелирует с характеристиками жирных хвостов.Эконометрически это означает, что временные ряды волатильности могут быть автокоррелированными, т.е. волатильность текущего периода может иметь некоторую связь с предыдущим периодом, вторым предыдущим периодом или даже третьим предыдущим периодом.

В [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

Выход[5]:

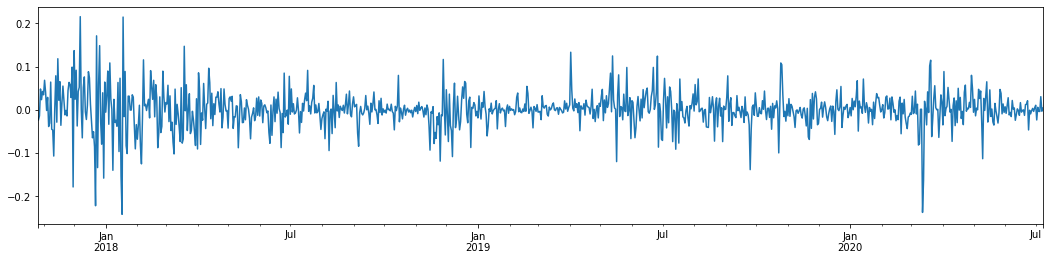
Если взять ежедневный логарифмический показатель доходности биткойна за последние 3 года и сопоставить его, можно четко увидеть феномен скопления волатильности. После бычьего рынка биткойна в 2018 году он был в стабильной позиции большую часть времени. Как мы можем видеть справа, в марте 2020 года, когда глобальные финансовые рынки рухнули, также произошел скачок ликвидности биткойна, причем доходность упала почти на 40% за день с резкими отрицательными колебаниями.

Одним словом, из интуитивного наблюдения мы можем видеть, что за большим колебанием будет следовать плотное колебание с большой вероятностью, что также является агрегирующим эффектом волатильности.

1-3. Подготовка данных

Чтобы подготовить набор выборки для обучения, сначала мы устанавливаем эталонную выборку, в которой логарифмическая ставка доходности является эквивалентной наблюдаемой волатильности.

Метод повторного отбора проб основан на почасовых данных.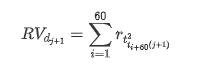

В [4]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

Выход[4]: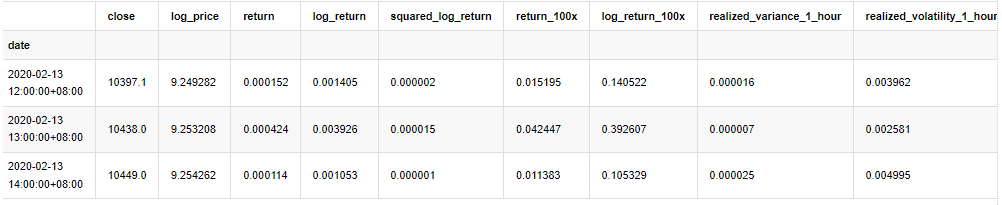

Приготовьте данные за пределами выборки таким же образом

В [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

Для понимания основных данных выборки проводится простой описательный анализ следующим образом:

В [9]:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

Выход[9]:

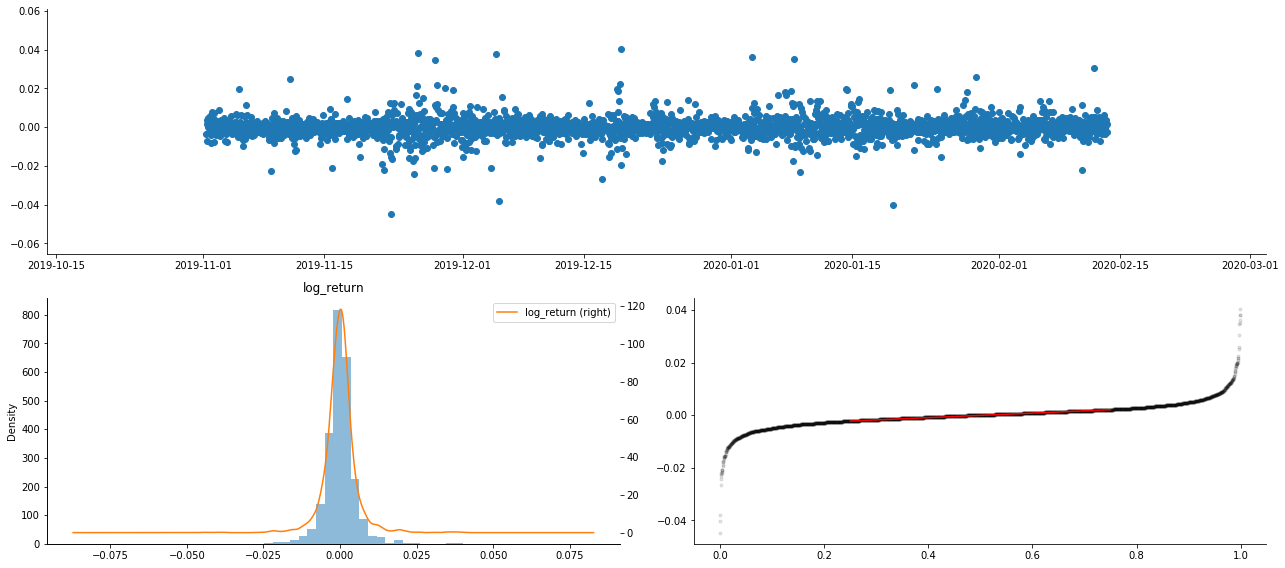
В результате в графике временных рядов логарифмической доходности наблюдается очевидная агрегация волатильности и эффект кредитного плеча.

Наклонность в диаграмме распределения логарифмических результатов меньше 0, что указывает на то, что результаты в выборке слегка отрицательны и предвзяты вправо.

Склонность распределения данных меньше 1, что указывает на то, что результаты внутри выборки слегка положительные и слегка уклоняются вправо.

Теперь, когда мы достигли этой точки, давайте сделаем еще один статистический тест. В [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

Выход[7]:

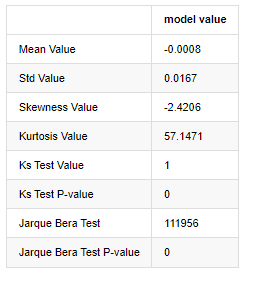
Используются статистические данные тестов Колмогорова - Смирнова и Ярке - Беры соответственно. Первоначальная гипотеза характеризуется значительной разницей и нормальным распределением. Если значение P меньше критического значения уровня доверия 0,05%, первоначальная гипотеза отклоняется.

Можно увидеть, что значение куртоза больше 3, что показывает характеристики толстых жировых хвостов. Значения P KS и JB меньше, чем доверительный интервал. Предположение о нормальном распределении отвергается, что доказывает, что коэффициент возврата BTC не имеет характеристик нормального распределения, а эмпирическое исследование имеет характеристики толстых жировых хвостов.

Сравнение реализованной и наблюдаемой волатильности

Для наблюдений мы объединяем квадрат_логи_возврат (логарифмическая доходность в квадрате) и реализованную_вариантность (реализованная вариантность).

В [11]:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

Выход[11]:

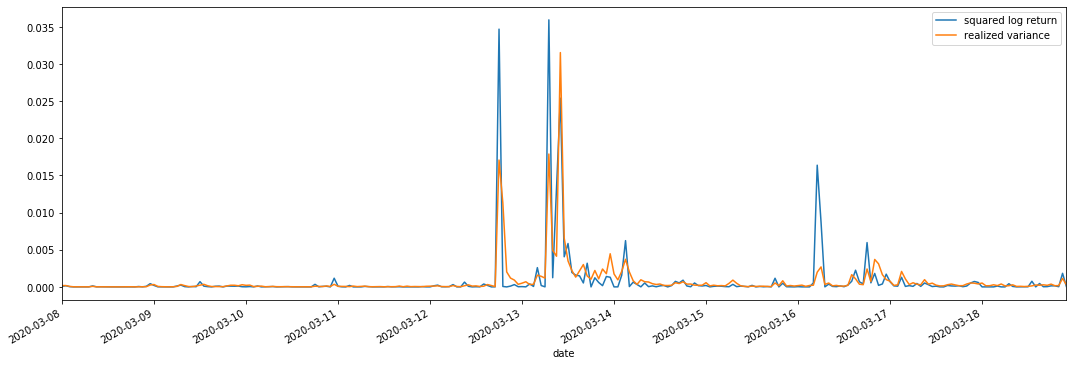
Можно увидеть, что когда диапазон реализованной вариантности больше, то волатильность диапазона ставки доходности также больше, а реализованная ставка доходности более плавная.

С чисто теоретической точки зрения RV ближе к реальной волатильности, в то время как краткосрочная волатильность сглаживается из-за того, что волатильность внутридневная относится к данным за одну ночь, поэтому с точки зрения наблюдения волатильность внутридневная более подходит для более низкой частоты волатильности фондового рынка.

2. Гладкость временных рядов

Если это нестационарный ряд, его необходимо приблизительно скорректировать к стационарному ряду. Общий способ - это обработка различий. Теоретически, после многократного различия, нестационарный ряд можно приблизить к стационарному ряду. Если ковариантность выборочного ряда стабильна, ожидание, вариантность и ковариантность его наблюдений не изменятся со временем, что указывает на то, что выборочный ряд более удобен для выводов в статистическом анализе.

При этом используется единый тест, а именно тест ADF. Для наблюдения за значимостью тест ADF использует тест t. В принципе, если серия не показывает очевидную тенденцию, сохраняются только постоянные элементы. Если серия имеет тенденцию, уравнение регрессии должно включать как постоянные элементы, так и элементы временного тренда. Кроме того, для оценки на основе информационных критериев можно использовать критерии AIC и BIC. Если требуется формула, то она выглядит следующим образом: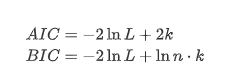

В [8]:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

Вне[8]: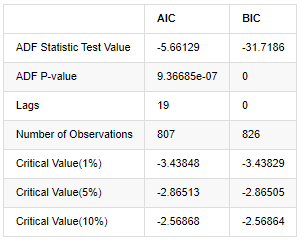

Первоначальное предположение заключается в том, что в рядах нет единого корня, то есть альтернативное предположение заключается в том, что ряд стационарный.

Идентификация модели и определение порядка

Для того чтобы установить уравнение среднего значения, необходимо провести тест автокорреляции на последовательности, чтобы убедиться, что термин ошибки не имеет автокорреляции.

В [19]:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

Выход[19]:

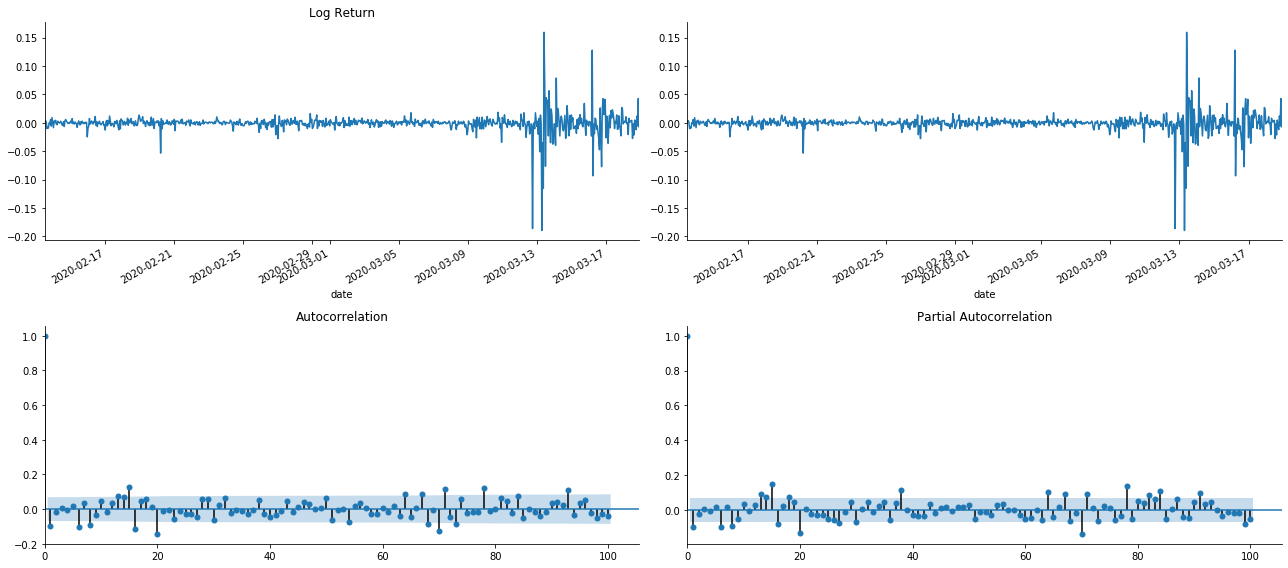
В то время эта картина дала мне вдохновение. Действительно ли рынок недействителен? Чтобы проверить, мы сделаем анализ автокорреляции на обратном ряду и определим порядок задержки модели.

Обычно используемый коэффициент корреляции измеряет корреляцию между ним и самим собой, то есть корреляцию между r(t) и r (t-l) в определенное время в прошлом: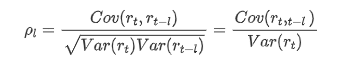

Тогда давайте сделаем количественный тест. Первоначальное предположение состоит в том, что все коэффициенты автокорреляции равны 0, то есть в рядах нет автокорреляции. Формула статистики теста написана следующим образом: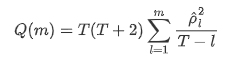

Для анализа было взято десять коэффициентов автокорреляции:

В [9]:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

Выход[9]: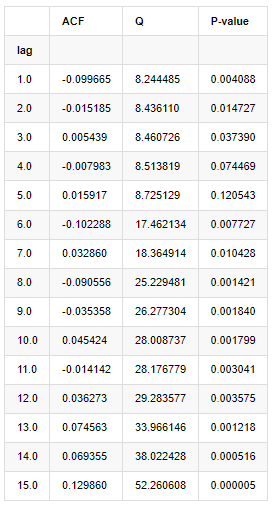

Согласно статистике испытаний Q и P-значения, мы можем видеть, что функция автокорреляции ACF постепенно становится 0 после порядка 0.

4. Моделирование ARMA

Модели AR и MA довольно просты. Проще говоря, Markdown слишком устал, чтобы писать формулы. Если вам интересно, пожалуйста, проверьте их сами. Модель AR (авторегрессия) в основном используется для моделирования временных рядов. Если серия прошла тест ACF, то есть коэффициент автокорреляции с интервалом 1 является значительным, то есть данные во времени могут быть полезны для прогнозирования времени t.

Модель MA (движущаяся средняя) использует случайные интерференции или предсказания ошибок прошлых q периодов для линейного выражения текущего значения предсказания.

Для полного описания динамической структуры данных необходимо увеличить порядок моделей AR или MA, но такие параметры сделают расчет более сложным.

Поскольку временные ряды цен обычно не стационарны, и эффект оптимизации метода разницы на стационарность был обсужден ранее, модель ARIMA (p, d, q) (сумма авторегрессивной скользящей средней) добавляет обработку разницы порядка d на основе применения существующих моделей к серии.

Одним словом, единственное отличие между моделью АРИМА и процессом построения модели АРМА заключается в том, что если после анализа стационарности получены нестабильные результаты, модель будет делать квадратную разницу в серии напрямую, а затем выполнять тест на стационарность, а затем определять порядок p и q, пока серия не стабилизируется. После построения модели и ее оценки будет сделан последующий прогноз, исключая шаг возвращения, чтобы сделать разницу. Однако разница в цене второго порядка бессмысленна, поэтому АРМА является лучшим выбором.

Выбор порядка

Далее, мы можем выбрать порядок непосредственно по информационному критерию, здесь мы попробуем это с термодинамической диаграммы AIC и BIC.

В [10]:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

Выход[10]: Наилучший параметр AIC: (0, 1, 1) Наилучший параметр BIC: (0, 1, 1) Наилучший параметр HQIC: (0, 1, 1) Лучший парам выбран: (0, 1, 1)

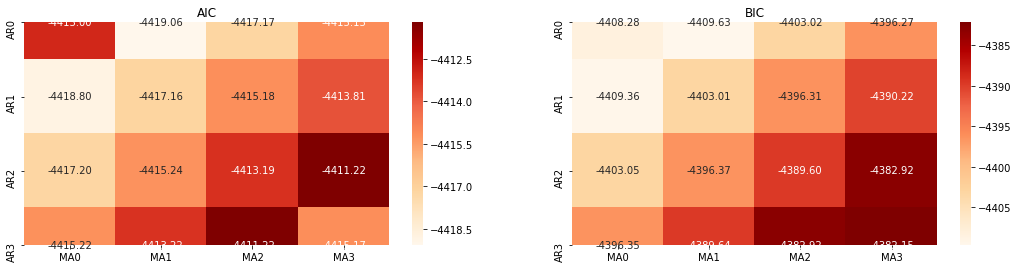
Очевидно, что оптимальная комбинация параметров первого порядка для логарифмической цены (0,1,1), что просто и просто. Log_return (логарифмическая скорость возврата) выполняет ту же операцию. Оптимальное значение AIC - (4,3), а оптимальное значение BIC - (0,1). Таким образом, оптимальная комбинация параметров для log_return (логарифмическая скорость возврата) - (0,1).

4-2 Моделирование и сопоставление ARMA

Квартальные коэффициенты не требуются, но SARIMAX богаче свойствами, поэтому было решено выбрать эту модель для моделирования и, кстати, провести описательный анализ следующим образом:

В [11]:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

Выход[11]: Результаты модели государственного пространства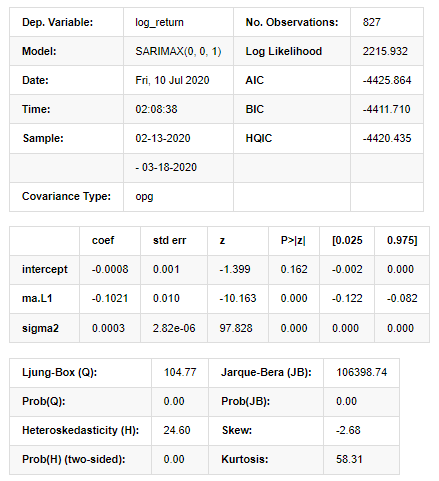

Предупреждения: [1] Матрица ковариантности, рассчитанная с использованием внешнего произведения градиентов (сложный шаг). В [27]:

model_results.plot_diagnostics(figsize=(18, 10));

Выход[27]:

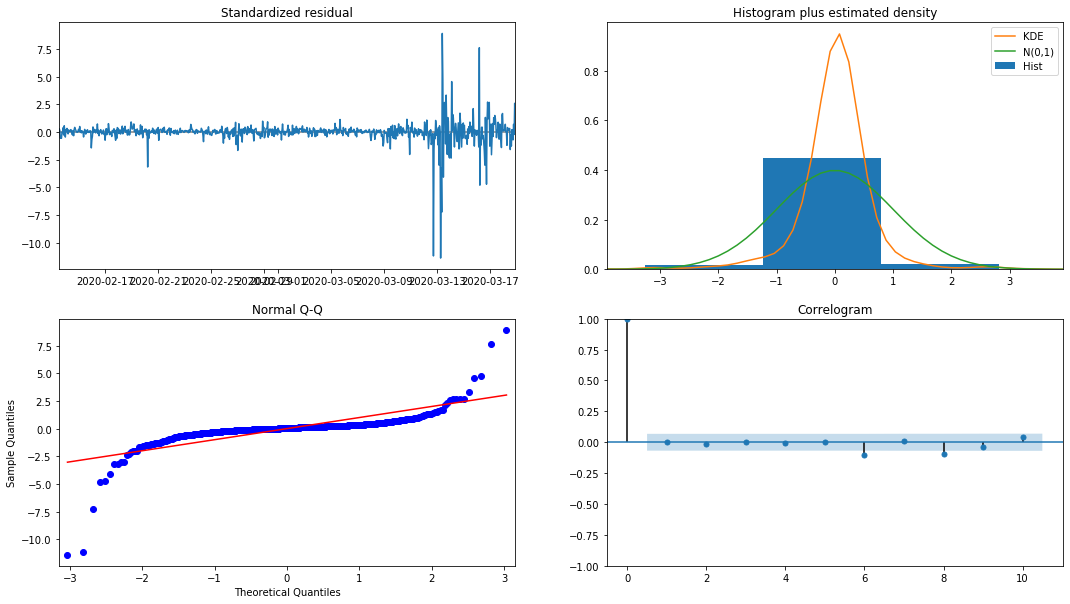
Плотность вероятности KDE в гистограмме далеко от нормального распределения N (0,1), что указывает на то, что остаток не является нормальным распределением.

В то же время необходимо проверить, может ли модель использоваться.

Испытание модели

Эффект совпадения остатка не идеален, поэтому мы провели тест Дурбина Уотсона на нем. Первоначальная гипотеза теста заключается в том, что последовательность не имеет автокорреляции, а последовательность альтернативной гипотезы является стационарной. Кроме того, если значения P тестов LB, JB и H меньше критического значения уровня доверия 0,05%, первоначальная гипотеза будет отвергнута.

В [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
root_test

Выход[12]: Испытание гетероскедастичности остатков (breakvar): stat=24,598, p=0.000

Нормальность испытаний остатков (жаркебера): stat=106398.739, p=0.000

Серийная корреляция остатков испытания (ljungbox): stat=104,767, p=0.000

Испытание Дурбина-Уотсона на остатки: d=2,00 (Примечание: 2 означает отсутствие последовательной корреляции, 0=pos, 4=neg)

Испытание для всех корней AR за пределами единичного круга (>1): верно

Испытание для всех корней MA за пределами единичного круга (>1): верно

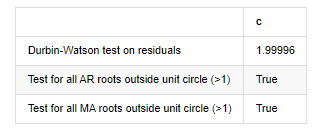
В [13]:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

Выход[13]:

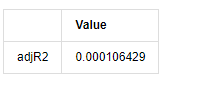
Если статистика теста Дарбина Уотсона равна 2, подтверждает, что серия не имеет корреляции, и ее статистическое значение распределяется между (0,4). Ближе к 0 означает, что положительная корреляция высока, в то время как близко к 4 означает, что отрицательная корреляция высока. Здесь она примерно равна 2.

В [14]:

model_results.params

Выход[14]: перехват -0.000817 ma.L1 -0.102102 Сигма2 0,000275 dтип: плавающий64

Подводя итог, этот параметр установки порядка может в основном удовлетворять требованиям моделирования временных рядов и последующего моделирования волатильности, но эффект соответствия таков-то.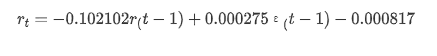

Прогноз модели

Далее обученная модель сопоставляется вперед. statsmodels предоставляет статические и динамические варианты сопоставления и прогнозирования. Разница заключается в том, используется ли значение наблюдения в следующем этапе прогнозирования или значение прогноза, генерируемое в предыдущем этапе, используется итеративно. Эффекты прогнозирования log_return (логитмическая скорость возврата) следующие:

В [37]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Выход[37]:

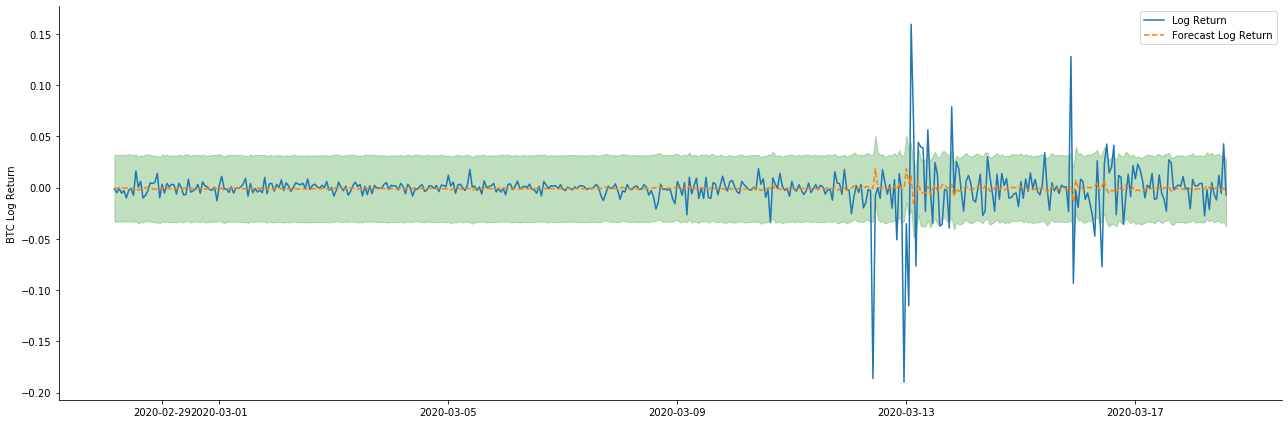
Видно, что эффект приспособления статического режима на выборку отличный, данные выборки могут быть почти охвачены 95% доверительным интервалом, а динамический режим немного неконтролируемый.

Итак, давайте посмотрим на эффект совпадения данных в динамическом режиме:

В [38]:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Выход[38]:

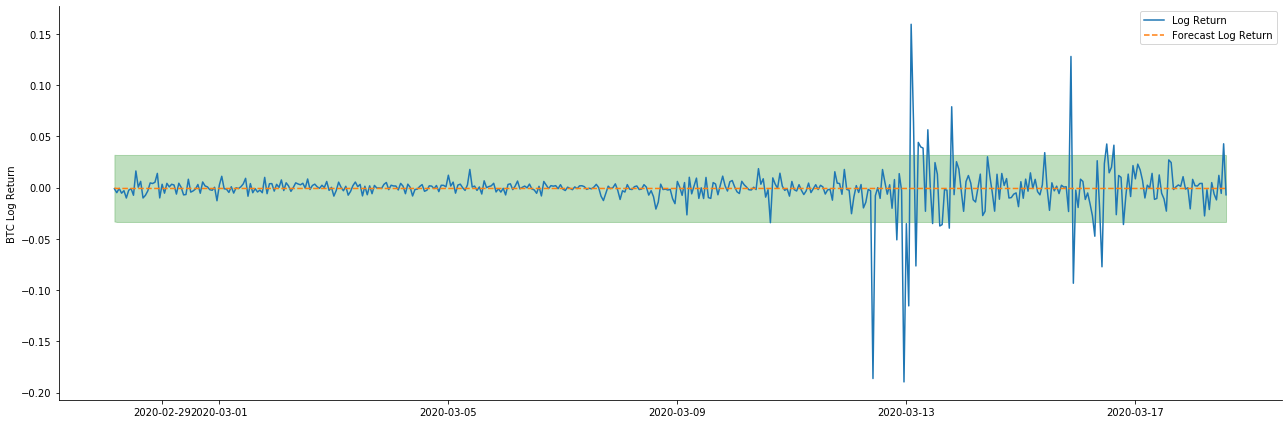
Можно увидеть, что эффект соответствия двух моделей на выборке превосходный, и среднее значение может быть почти покрыто 95%-ным доверительным интервалом, но статическая модель, очевидно, более подходящая.

В [41]:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Выход[41]:

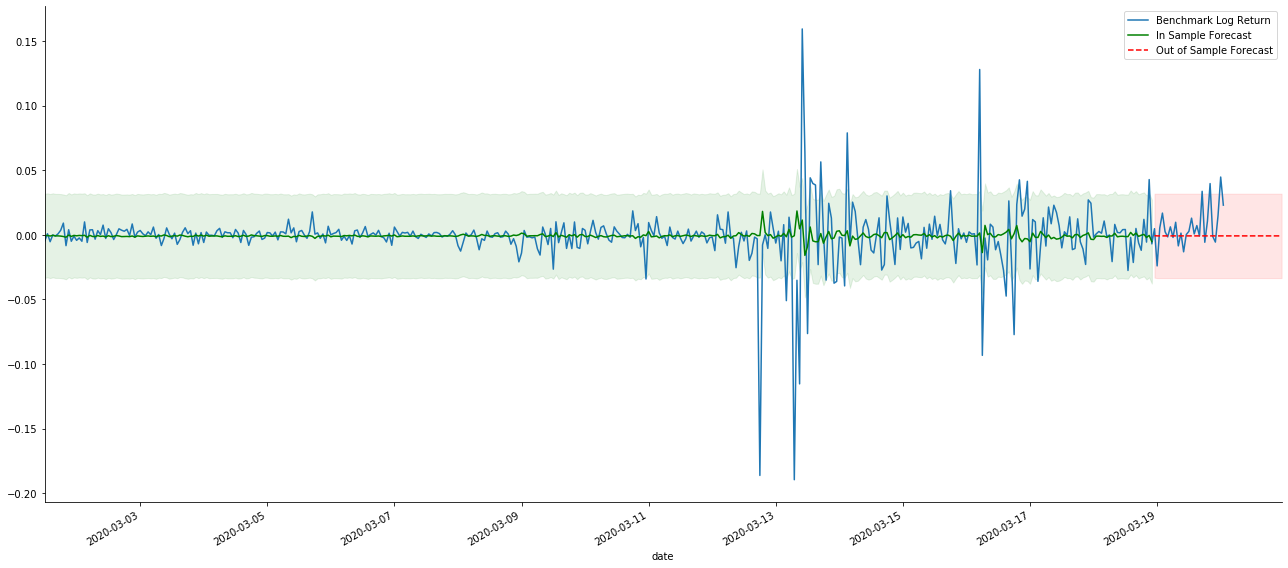
Поскольку совпадение данных в выборке является прогрессивным предсказанием, когда количество информации в выборке достаточно, статическая модель склонна к чрезмерному совпадению, в то время как динамической модели не хватает надежных зависимых переменных, и эффект становится все хуже и хуже после итерации.

Если мы перевернем прогноз доходности на log_price (логарифмическая цена), совпадение показывается на рисунке ниже:

В [42]:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

Выход[42]:

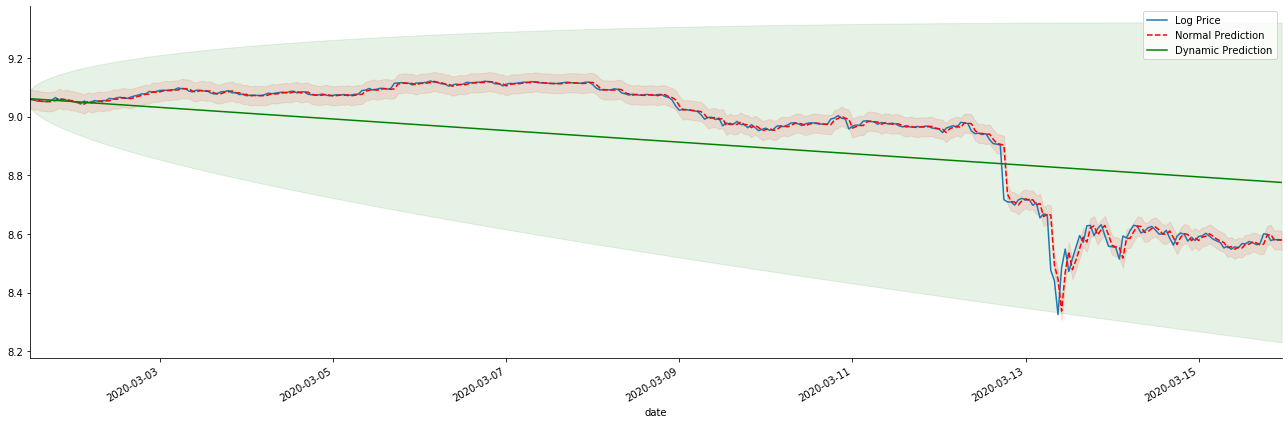
Легко увидеть совпадающие преимущества статической модели и крайнюю разницу между динамической и статической моделью в долгосрочном прогнозировании. Красная пунктирная линия и розовый диапазон... Вы не можете сказать, что прогноз этой модели неверен. В конце концов, она полностью охватывает тенденцию скользящей средней, но... имеет ли это смысл?

На самом деле, сама модель ARMA не ошибается, потому что проблема заключается не в самой модели, а в объективной логике самих вещей. Модель временных рядов может быть установлена только на основе корреляции между предыдущими и последующими наблюдениями. Поэтому невозможно моделировать серию белого шума. Поэтому вся предыдущая работа основана на смелом предположении, что серия показателей доходности BTC не может быть независимой и идентично распределенной.

В целом, серии показателей доходности являются сериями мартингейловских различий, что означает, что показатели доходности непредсказуемы, а предположение о слабой эффективности соответствующего рынка сохраняется.

Однако совпадающая остаточная последовательность также является последовательностью мартингейловских различий. Последовательность мартингейловских различий может быть не независимой и идентично распределенной, но условная вариантность может зависеть от прошлого значения, поэтому автокорреляция первого порядка исчезла, но все еще существует автокорреляция более высокого порядка, которая также является важным условием для моделирования и наблюдения волатильности.

Если такая логика верна, то предпосылка построения различных моделей волатильности также верна. Так что для ряда показателей доходности, если слабая эффективность рынка удовлетворена, то среднее значение должно быть трудно предсказать, но вариантность предсказуема.

Наконец, давайте просто оценить эффект предсказания: с ошибкой в качестве критерия оценки показатели внутри и вне выборки следующие:

В [15]:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

Выход[15]: Ошибка среднего квадратного корня (RMSE): 0,0184 Ошибка среднего квадратного корня (RMSE): 0,0167 Средняя абсолютная процентная ошибка (MAPE): 2,25e+03 Средняя абсолютная процентная ошибка (MAPE): 395

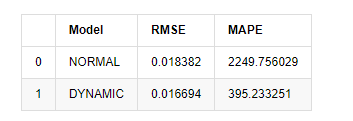
Можно увидеть, что статическая модель немного лучше динамической модели с точки зрения совпадения ошибок между прогнозируемым значением и реальным значением. Она хорошо соответствует логарифмическому уровню возврата биткойна, что в основном соответствует ожиданиям. Динамическому прогнозу не хватает более точной переменной информации, а ошибка также увеличивается итерацией, поэтому эффект прогнозирования плохой. MAPE больше 100%, поэтому фактическое качество соответствия обеих моделей не идеально.

В [18]:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

Выход[18]:

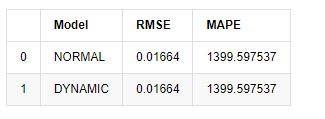
Поскольку следующее предсказание за пределами выборки зависит от результатов предыдущего шага, эффективной является только динамическая модель.

Подводя итог, статическая модель модели ARMA подходит для сопоставления внутривыборочного показателя доходности биткойна. Краткосрочное предсказание показателя доходности может эффективно покрывать доверительный интервал, но долгосрочное предсказание очень сложно, что удовлетворяет слабой эффективности рынка. После тестирования показатель доходности в пределах выборочного интервала удовлетворяет предпосылке последующего наблюдения за волатильностью.

5. Эффект ARCH

Эффект модели ARCH - это серийная корреляция условной последовательности гетероцедастичности. Тест смеси Ljung Box используется для проверки корреляции остаточных квадратных рядов, чтобы определить, есть ли эффект ARCH. Если тест эффекта ARCH пройден, то есть серия имеет гетероцедастичность, следующий шаг моделирования GARCH может быть выполнен для совместной оценки среднего уравнения и уравнения волатильности. В противном случае модель должна быть оптимизирована и скорректирована, например, дифференциальная обработка или взаимные серии.

Мы готовим несколько наборов данных и глобальных переменных здесь:

В [33]:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

Выход[33]:

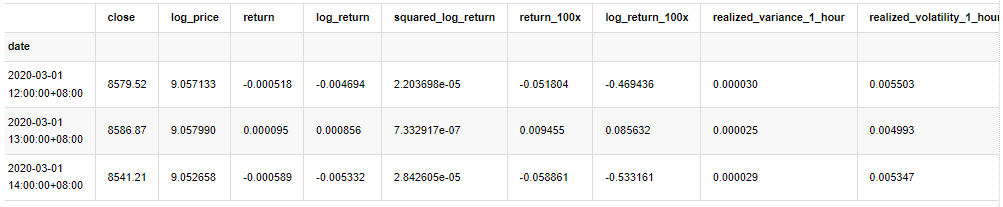
В [22]:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

Выход[22]: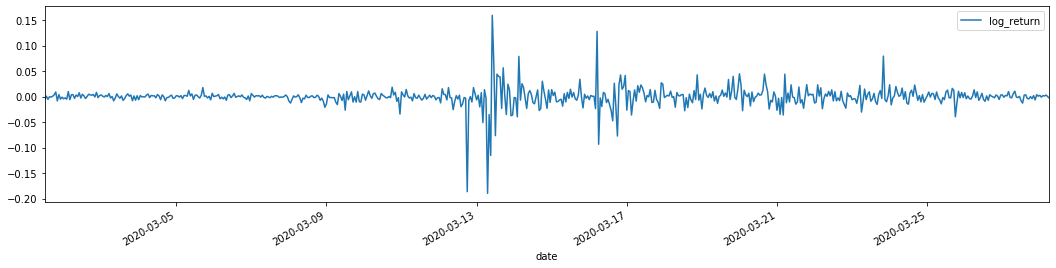

Логарифмические показатели возврата показаны выше. Далее нам нужно проверить эффект ARCH выборки. Мы устанавливаем остаточный ряд в выборке на основе ARMA. Некоторые серии и квадратный ряд остаточного и остаточного вычисляются сначала:

В [20]:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

Выход[20]:

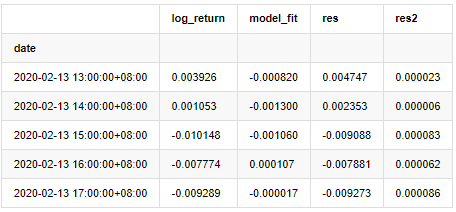
Затем графикуется остаточный ряд выборки.

В [69]:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

Выход[69]:

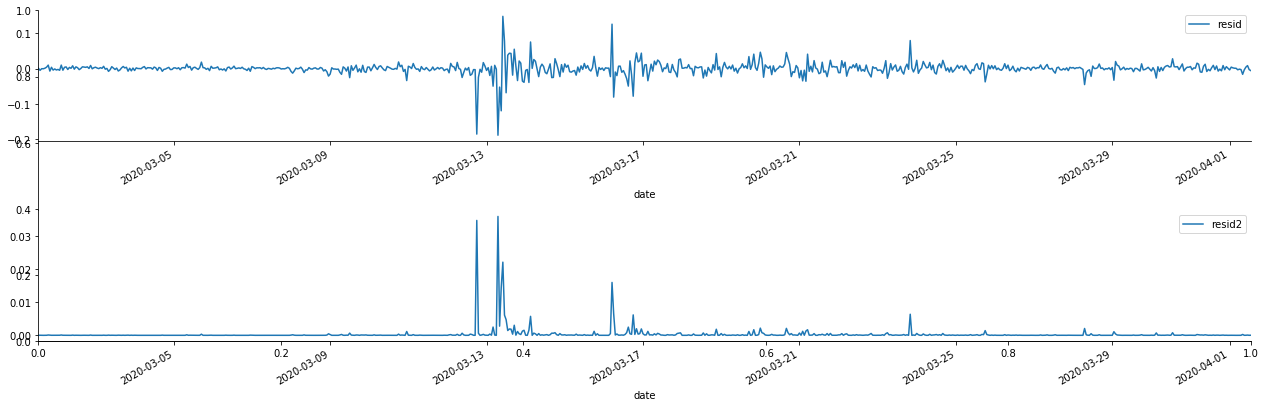
Можно увидеть, что остаточный ряд имеет явные характеристики агрегации, и можно первоначально судить, что ряд имеет эффект ARCH.

В [70]:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

Выход[70]:

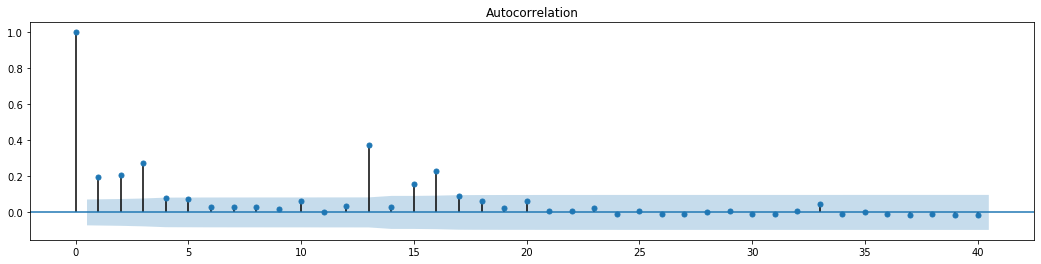
Первоначальное предположение для теста смешивания рядов заключается в том, что ряд не имеет корреляции. Можно увидеть, что соответствующие значения P первых 20 порядков данных меньше критического значения уровня доверия 0,05%. Поэтому первоначальное предположение отвергается, то есть остаток ряда имеет эффект ARCH. Модель вариантности может быть установлена с помощью модели типа ARCH, чтобы соответствовать гетероцедастичности остаточного ряда и предсказать волатильность.

6. Моделирование GARCH

Прежде чем выполнять моделирование GARCH, мы должны иметь дело с жирной хвостовой частью ряда. Поскольку термин ошибки ряда в гипотезе должен соответствовать нормальному распределению или t-распределению, и мы ранее проверили, что серия урожая имеет жирный хвостовой распределение, поэтому нам нужно описать и дополнить эту часть.

В моделировании GARCH элемент ошибки предоставляет варианты нормального распределения, t-распределения, GED (Generalized Error Distribution) и skewed Students t-распределения.

Связанные

Больше