Торговля парами на основе технологии, основанной на данных

Торговля парами на основе технологии, основанной на данных

Торговля парами является хорошим примером формулирования торговых стратегий на основе математического анализа.

Основные принципы

Предположим, у вас есть пара инвестиционных целей X и Y, которые имеют некоторые потенциальные связи. Например, две компании производят одни и те же продукты, такие как Pepsi Cola и Coca Cola. Вы хотите, чтобы соотношение цен или базовые спрэды (также известные как разница в ценах) обоих оставались неизменными с течением времени. Однако из-за временных изменений спроса и предложения, таких как большой заказ на покупку/продажу инвестиционной цели и реакция на важные новости одной из компаний, разница в ценах между двумя парами может время от времени отличаться. В этом случае один инвестиционный объект движется вверх, а другой движется вниз относительно друг друга. Если вы хотите, чтобы это несогласие вернулось к нормальному с течением времени, вы можете найти торговые возможности (или возможности арбитража). Такие возможности арбитража можно найти везде на рынке цифровой валюты или на внутреннем рынке товарных фьючерсов, таких как отношения между BTC и безопасными гаваньями; отношения между со

Когда возникает временная разница в цене, вы продаете инвестиционный объект с отличными показателями (повышающийся инвестиционный объект) и покупаете инвестиционный объект с плохими показателями (падающий инвестиционный объект). Вы уверены, что процентная маржа между двумя инвестиционными объектами в конечном итоге упадет из-за падения инвестиционного объекта с отличными показателями или роста инвестиционного объекта с плохими показателями или обоих. Ваша сделка будет приносить деньги во всех этих похожих ситуациях. Если инвестиционные объекты движутся вверх или вниз вместе, не изменяя разницу в цене между ними, вы не будете делать или терять деньги.

Таким образом, торговля парами является нейтральной для рынка стратегией торговли, позволяющей трейдерам получать прибыль практически от любых рыночных условий: тенденции роста, тенденции снижения или горизонтальной консолидации.

Объясните понятие: две гипотетические инвестиционные цели

• Построить нашу исследовательскую среду на платформе FMZ Quant

Прежде всего, для того, чтобы работать беспрепятственно, нам необходимо создать нашу исследовательскую среду.FMZ.COM) для создания нашей исследовательской среды, в основном для использования удобного и быстрого интерфейса API и хорошо упакованной системы Docker этой платформы позже.

В официальном названии платформы FMZ Quant эта система Docker называется системой Docker.

Пожалуйста, ознакомьтесь с моей предыдущей статьей о том, как развернуть докер и робота:https://www.fmz.com/bbs-topic/9864.

Читатели, которые хотят приобрести собственный сервер облачных вычислений для развертывания докеров, могут обратиться к этой статье:https://www.fmz.com/digest-topic/5711.

После успешного развертывания сервера облачных вычислений и системы докеров, следующим мы установим самый большой артефакт Python: Anaconda.

Чтобы реализовать все соответствующие программные среды (библиотеки зависимостей, управление версиями и т. д.), необходимые в этой статье, самый простой способ - использовать Anaconda.

Для установки Anaconda, пожалуйста, обратитесь к официальному руководству Anaconda:https://www.anaconda.com/distribution/.

В этой статье также будут использованы numpy и панды, две популярные и важные библиотеки в научном вычислении Python.

Вышеуказанная основная работа также может относиться к моим предыдущим статьям, в которых представлено, как настроить среду Anaconda и библиотеки numpy и pandas.https://www.fmz.com/bbs-topic/9863.

Далее, давайте используем код для реализации двух гипотетических инвестиционных целей:

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Да, мы также будем использовать matplotlib, очень известную библиотеку графиков в Python.

Давайте сгенерируем гипотетическую инвестиционную цель X, и смоделируем и наметим ее ежедневную доходность через нормальное распределение.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

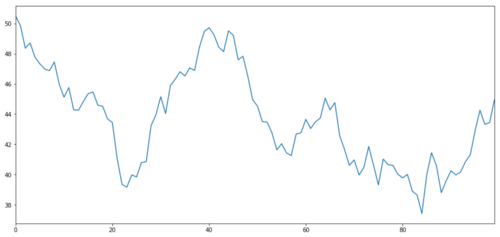
Х объекта инвестиций моделируется для того, чтобы составить график его ежедневной доходности по нормальному распределению

Теперь мы генерируем Y, который сильно интегрирован с X, поэтому цена Y должна быть очень похожа на изменение X. Мы моделируем это, беру X, перемещая его вверх и добавляя какой-то случайный шум, извлеченный из нормального распределения.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

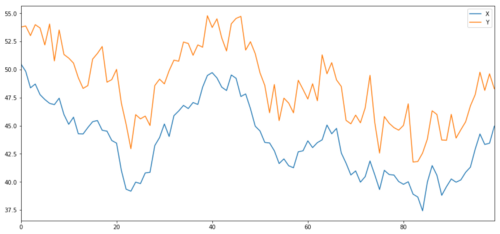
X и Y объекта инвестиций в коинтеграцию

Коинтеграция

Коинтеграция очень похожа на корреляцию, что означает, что соотношение между двумя сериями данных изменится близко к среднему значению.

Y = X + e

где - это постоянное соотношение и e - шум.

Для пар, торгующих между двумя временными рядами, ожидаемое значение соотношения с течением времени должно сходиться со средним значением, то есть они должны быть соинтегрированы.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

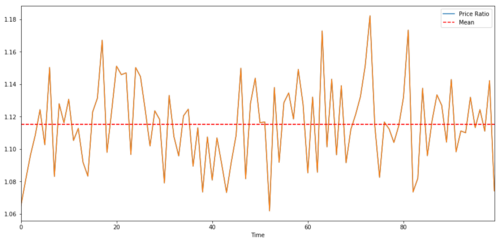
Соотношение и средняя стоимость между двумя интегрированными целевыми ценами инвестиций

Испытание коинтеграции

Удобный метод тестирования - использовать statsmodels.tsa.stattools. Мы увидим очень низкое значение p, потому что мы создали два серии данных искусственно, которые максимально интегрированы.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Результат: 1.81864477307e-17

Примечание: корреляция и коинтеграция

Корреляция и коинтеграция, хотя и похожи в теории, не одно и то же. Давайте посмотрим на примеры соответствующих, но не коинтегрированных рядов данных и наоборот.

X.corr(Y)

Результат: 0,951

Как и ожидалось, это очень высокое число. Но что насчет двух связанных, но не соинтегрированных рядов? Простой пример - это ряд двух отклоняющихся данных.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

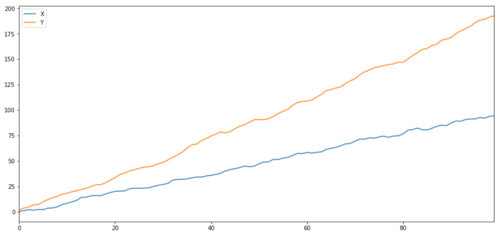
Две связанные серии (не интегрированные вместе)

Коэффициент корреляции: 0,998 P-значение теста соинтеграции: 0,258

Простыми примерами коинтеграции без корреляции являются последовательности нормального распределения и квадратные волны.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

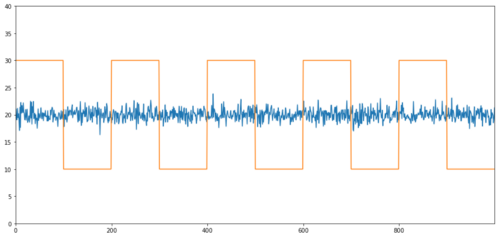
Корреляция: 0,007546 Значение P испытания соинтеграции: 0,0

Корреляция очень низкая, но значение p показывает идеальную коинтеграцию!

Как проводить торговлю парами?

Поскольку два совместно интегрированных временных ряда (например, X и Y выше) стоят друг против друга и отклоняются друг от друга, иногда базовые спреды высоки или низки. Мы проводим пару торговли, покупая один инвестиционный объект и продавая другой. Таким образом, если две инвестиционные цели падают или растут вместе, мы не будем ни зарабатывать деньги, ни терять деньги, то есть мы нейтральны на рынке.

Возвращаясь к вышеизложенному, X и Y в Y = X + e, так что соотношение (Y / X) движется вокруг его среднего значения . Мы зарабатываем деньги через соотношение реверсии среднего значения. Для этого мы обратим внимание на случай, когда X и Y далеко друг от друга, то есть значение слишком высокое или слишком низкое:

• Увеличение соотношения: это когда соотношение очень маленькое и мы ожидаем, что оно увеличится.

• Соотношение шорта: это когда соотношение очень большое и мы ожидаем, что оно уменьшится.

Пожалуйста, обратите внимание, что у нас всегда есть позиция хеджирования: если субъект торговли покупает потери, короткая позиция будет приносить деньги, и наоборот, поэтому мы защищены от общей тенденции рынка.

Если X и Y объекта торговли движутся относительно друг друга, мы будем делать деньги или терять деньги.

Использовать данные для поиска торговых объектов с аналогичным поведением

Лучший способ сделать это - начать с субъекта торговли, который вы подозреваете может быть коинтеграцией и провести статистический тест.многократная предвзятость.

Многократное предвзятое сравнениеотносится к увеличенной вероятности неправильного получения важных значений p при выполнении многих тестов, потому что нам нужно выполнять большое количество тестов. Если мы выполним 100 тестов на случайных данных, мы должны увидеть 5 значений p ниже 0,05. Если вы хотите сравнить n торговых целей для коинтеграции, вы будете выполнять n (n-1) / 2 сравнения, и вы увидите много неправильных значений p, которые увеличатся с увеличением ваших тестовых образцов. Чтобы избежать этой ситуации, выберите несколько торговых пар и у вас есть причина определить, что они могут быть коинтеграцией, а затем проверить их отдельно. Это значительно уменьшитмногократная предвзятость.

Поэтому давайте попробуем найти некоторые торговые цели, которые показывают коинтеграцию. Давайте возьмем корзину крупных американских технологических акций в индексе S&P 500 в качестве примера. Эти торговые цели работают в похожих сегментах рынка и имеют цены коинтеграции. Мы сканируем список торговых объектов и тестируем коинтеграцию между всеми парами.

возвращенная матрица результатов теста коинтеграции, матрица p-значения и все пары с p-значением менее 0,05.Этот метод склонен к многократному сравнению, так что на самом деле, они должны провести вторую проверку.В этой статье, для удобства нашего объяснения, мы предпочитаем игнорировать этот момент в примере.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Примечание: Мы включили рыночный показатель (SPX) в данные - рынок управляет потоком многих торговых объектов. Обычно вы можете найти два торговых объекта, которые кажутся соединенными; но на самом деле они не соединяются друг с другом, а с рынком. Это называется смешивающей переменной. Важно проверить участие рынка в любом отношениях, которые вы найдете.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Теперь давайте попробуем использовать наш метод для поиска коинтегрированных торговых пар.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

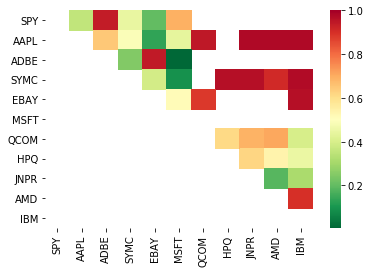
Похоже, что ADBE и MSFT соединены. Давайте посмотрим на цену, чтобы убедиться, что это действительно имеет смысл.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

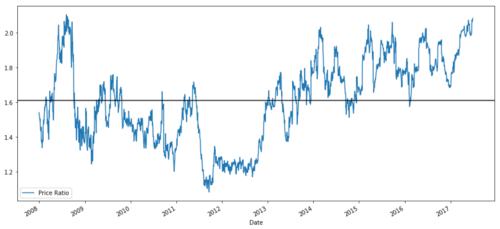
График соотношения цен между MSFT и ADBE с 2008 по 2017 год

Это соотношение действительно выглядит как стабильное среднее. Абсолютные соотношения не являются статистически полезными. Более полезно стандартизировать наши сигналы, обращаясь с ними как с Z Score. Z Score определяется как:

Показатель Z (значение) = (значение среднее значение) / стандартное отклонение

Предупреждение

Фактически, мы обычно пытаемся расширить данные на предпосылке, что данные распределены нормально. Однако многие финансовые данные не распределены нормально, поэтому мы должны быть очень осторожны, чтобы не просто предположить нормальность или какое-либо конкретное распределение при создании статистики. Истинное распределение соотношений может иметь эффект жирного хвоста, и эти данные, которые имеют тенденцию быть крайними, сбивают с толку нашу модель и приводят к огромным потерям.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

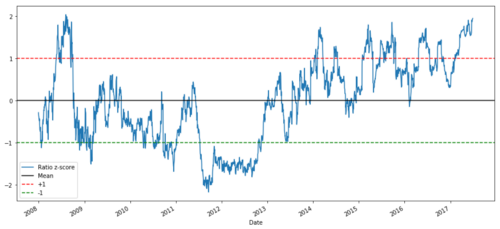
Соотношение цен Z между MSFT и ADBE с 2008 по 2017 год

Теперь нам легче наблюдать движение соотношения близко к среднему значению, но иногда легко иметь большую разницу от среднего значения.

Теперь, когда мы обсудили базовые знания стратегии торговли парами и определили предмет совместной интеграции на основе исторической цены, давайте попробуем разработать торговый сигнал.

• Сбор достоверных данных и очистка данных;

• Создание функций из данных для идентификации торговых сигналов/логики;

• Функции могут быть скользящими средними или данными о ценах, корреляциями или соотношениями более сложных сигналов - объединяют их для создания новых функций;

• Используйте эти функции для генерации торговых сигналов, то есть, какие сигналы покупают, продают или короткую позицию наблюдать.

К счастью, у нас есть платформа FMZ Quant (fmz.comДля разработчиков стратегии это большое благословение: мы можем посвятить свои силы и время разработке логики стратегии и расширению функций.

В платформе FMZ Quant есть инкапсулированные интерфейсы для различных основных бирж. Что нам нужно сделать, так это назвать эти интерфейсы API. Остальная часть логики реализации была завершена профессиональной командой.

Для того, чтобы завершить логику и объяснить принцип в этой статье, мы представим эти основные логики подробно.

Давайте начнем:

Шаг 1: Задайте свой вопрос

Здесь мы пытаемся создать сигнал, чтобы сказать нам, будет ли соотношение покупать или продавать в следующий момент, то есть наша переменная предсказания Y:

Y = соотношение покупать (1) или продавать (-1)

Y ((t) = Sign ((Ratio ((t+1) Ratio ((t))

Обратите внимание, что нам не нужно предсказывать фактическую целевую цену сделки или даже фактическое значение коэффициента (хотя мы можем), но только направление коэффициента на следующем этапе.

Шаг 2: Сбор достоверных и точных данных

FMZ Quant - ваш друг! Вам нужно только указать объект транзакции, который будет торговаться, и источник данных, который будет использоваться, и он извлечет необходимые данные и очистит их для разделения дивидендов и объектов транзакций.

По дням торгов за последние 10 лет (около 2500 точек данных) мы получили следующие данные с помощью Yahoo Finance: цена открытия, цена закрытия, самая высокая цена, самая низкая цена и объем торгов.

Шаг 3: Разделите данные

Не забывайте об этом очень важном этапе в тестировании точности модели.Мы используем следующие данные для обучения/валидации/испытания.

• Обучение 7 лет ~ 70%

• Испытание ~ 3 года 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

В идеале, мы также должны создавать наборы проверки, но мы не будем делать этого сейчас.

Шаг 4: Инженерия характеристик

Какими могут быть связанные функции? Мы хотим предсказать направление изменения коэффициента. Мы видели, что наши две торговые цели соинтегрированы, поэтому это соотношение имеет тенденцию смещаться и возвращаться к среднему значению. Похоже, что наши характеристики должны быть некоторыми мерами среднего коэффициента, и разница между текущим значением и средним значением может генерировать наш торговый сигнал.

Мы используем следующие функции:

• коэффициент скользящей средней за 60 дней: измерение скользящей средней;

• коэффициент пятидневного скользящего среднего: измерение текущего значения среднего;

• стандартное отклонение в 60 дней;

• Показатель Z: (5d MA - 60d MA) / 60d SD.

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

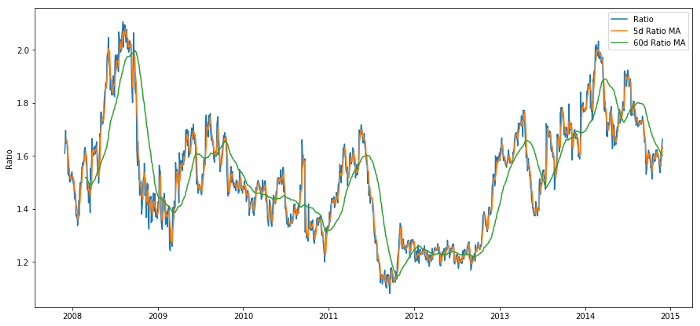
Соотношение цен между 60d и 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

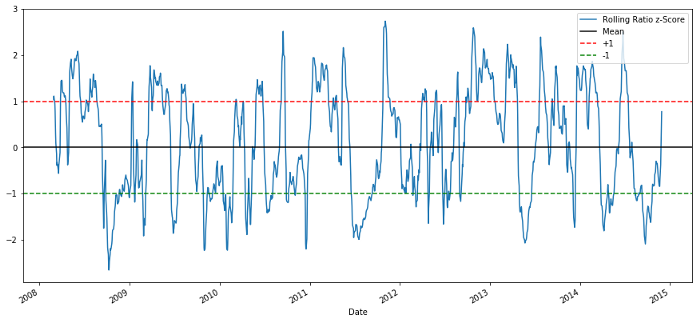
60-5 Z Показатель коэффициентов цен

Показатель Z от значения скользящей средней выявляет свойство регрессии среднего значения соотношения!

Шаг 5: Выбор модели

Давайте начнем с очень простой модели. Если посмотреть на график Z-баллов, мы увидим, что если Z-балл слишком высокий или слишком низкий, он вернется. Давайте используем +1/-1 в качестве порога для определения слишком высокого и слишком низкого, а затем мы можем использовать следующую модель для генерации торговых сигналов:

• Когда z ниже -1.0, соотношение покупается (1), потому что мы ожидаем, что z вернется к 0, поэтому соотношение увеличивается;

• Когда z выше 1,0, соотношение продается (- 1), потому что мы ожидаем, что z вернется к 0, поэтому соотношение уменьшается.

Шаг 6: Обучение, проверка и оптимизация

Наконец, давайте посмотрим на фактическое влияние нашей модели на фактические данные.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

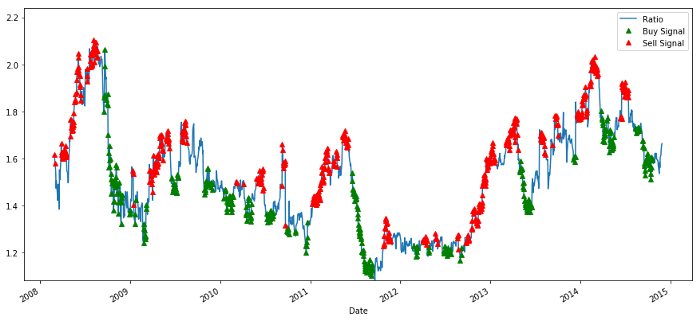
Сигнал соотношения цены покупки и продажи

Сигнал кажется разумным. Мы, кажется, продаем, когда он высокий или увеличивается (красные точки) и покупаем его обратно, когда он низкий (зеленые точки) и уменьшается. Что это означает для фактического предмета нашей сделки?

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

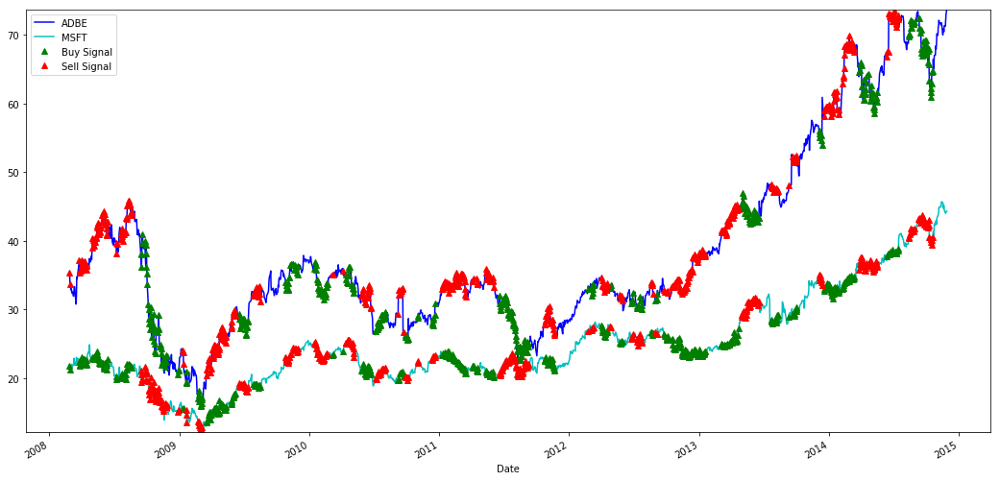
Сигналы на покупку и продажу акций МСФТ и АДБЕ

Обратите внимание на то, как мы иногда получаем прибыль на коротких ногах, иногда на длинных ногах, а иногда и то и другое.

Мы удовлетворены сигналом обучающих данных. Давайте посмотрим, какой вид прибыли может генерировать этот сигнал. Когда соотношение низкое, мы можем сделать простой обратный тестер, купить соотношение (купить 1 ADBE акции и продать соотношение x MSFT акции), и продать соотношение (продать 1 ADBE акции и купить x соотношение MSFT акции), когда оно высокое, и рассчитать PnL транзакции этих соотношений.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Результат: 1783,375

Итак, эта стратегия, кажется, выгодна! Теперь мы можем еще больше оптимизировать, изменив скользящее среднее временное окно, изменив пороги покупки/продажи и закрытия позиций, и проверить улучшение производительности данных проверки.

Мы также можем попробовать более сложные модели, такие как логистическая регрессия и SVM, чтобы предсказать 1/- 1.

Теперь, давайте продвинем эту модель, которая приводит нас к:

Шаг 7: обратная проверка данных испытания

Опять же, платформа FMZ Quant использует высокопроизводительный двигатель обратного тестирования QPS / TPS, чтобы действительно воспроизвести историческую среду, устранить распространенные ловушки количественного обратного тестирования и вовремя обнаружить недостатки стратегий, чтобы лучше помочь реальным инвестициям бота.

Для того чтобы объяснить принцип, в этой статье все еще выбирается показать основную логику. В практическом применении мы рекомендуем читателям использовать платформу FMZ Quant. В дополнение к экономии времени, важно улучшить уровень допуска ошибок.

Мы можем использовать вышеприведенную функцию, чтобы просмотреть PnL данных теста.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

Результат: 5262 868

Эта модель проделала отличную работу, она стала нашей первой простой моделью торговли парами.

Избегайте чрезмерного приспособления

Прежде чем завершить дискуссию, я хотел бы обсудить, в частности, о перенастройке. Перенастройка является самой опасной ловушкой в торговых стратегиях. Алгоритм перенастройки может очень хорошо работать в бэкстестесте, но не работает на новых невидимых данных - что означает, что он на самом деле не показывает никакой тенденции данных и не имеет реальной способности к прогнозированию.

В нашей модели мы используем прокатные параметры для оценки и оптимизации длины временного окна. Мы можем решить просто повторить все возможности, разумный промежуток времени и выбрать продолжительность времени в соответствии с лучшей производительностью нашей модели. Давайте напишем простую петлю, чтобы набрать длину временного окна в соответствии с pnl данных обучения и найти лучшую петлю.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Теперь мы исследуем производительность модели на данных теста, и мы обнаруживаем, что эта длина временного окна далеко не оптимальна! Это потому, что наш первоначальный выбор явно перегрузил данные выборки.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Очевидно, что данные выборки, подходящие для нас, не всегда дадут хорошие результаты в будущем.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

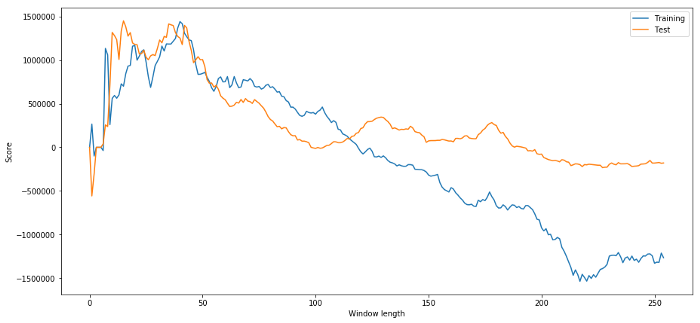
Мы видим, что любая вещь от 20 до 50 является хорошим выбором для окна времени.

Чтобы избежать перенастройки, мы можем использовать экономические рассуждения или характер алгоритма для выбора длины временного окна. Мы также можем использовать фильтр Калмана, который не требует от нас указания длины; Этот подход будет описан позже в другой статье.

Следующий шаг

В этой статье мы предлагаем несколько простых методов введения, чтобы продемонстрировать процесс разработки торговых стратегий. На практике следует использовать более сложную статистику.

• Экспонент Хёрста;

• период полураспада средней регрессии, выведенный из процесса Орнштейна-Уленбека;

• Калманский фильтр.

Связанные

Больше