Марковская цепь вероятность переходного состояния количественная торговая стратегия

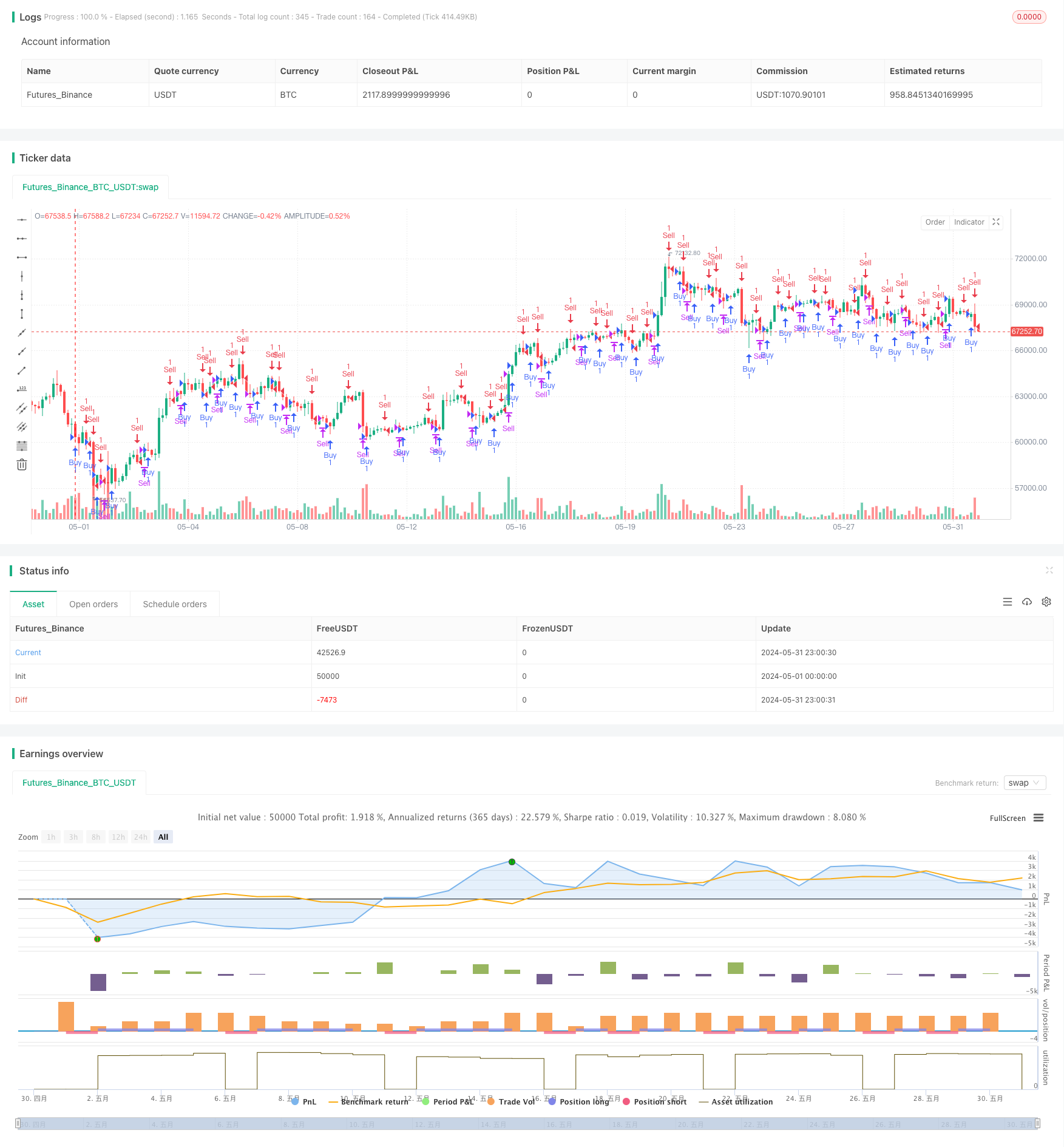
Обзор

Стратегия количественного трейдинга с преобразованием состояния в вероятность Марковской цепочки - это инновационный метод трейдинга, основанный на модели Марковской цепочки. Стратегия использует вероятность преобразования состояния в Марковской цепочке для прогнозирования движения рынка и принятия торговых решений на основе этого.

Уникальность данного метода заключается в том, что он учитывает не только текущее состояние рынка, но и динамику перехода между состояниями рынка. Благодаря введению вероятностных моделей, стратегия может лучше улавливать неопределенность и волатильность рынка, что позволяет принимать более гибкие и адаптивные торговые решения в различных рыночных условиях.

Стратегический принцип

1. Определение состояния: стратегия определяет состояние рынка в трех типах - бычьем (высокий), медленном (низкий) и горизонтальном (устойчивый). Эти состояния определяются путем сравнения текущей ценой закрытия с предыдущей ценой закрытия.

2. Вероятность преобразования: стратегия использует 9 входных параметров для определения вероятности преобразования между различными состояниями. Например,prob_bull_to_bullВероятность сохранения бычьего рынка.

3. Логика преобразования состояния: стратегия использует упрощенную логику преобразования для моделирования процесса преобразования состояния в цепочке Марковых. Она использует счетчикtransition_counterДля моделирования вероятностного преобразования.

4. Генерирование торговых сигналов: на основе текущего состояния стратегия генерирует сигналы о покупке, продаже или устранении позиций. Когда состояние бычьего рынка, стратегия начинает делать больше; когда состояние медвежьего рынка, стратегия начинает делать пусто; когда состояние горизонтального, стратегия устраняет все позиции.

Стратегические преимущества

1. Вероятностная модель: с помощью внедрения модели цепочки Маркова стратегия лучше улавливает случайность и неопределенность рынка, что трудно достичь традиционными методами технического анализа.

2. Гибкость: стратегия может быть адаптирована к различным рыночным условиям путем корректировки параметров вероятности конверсии, что делает ее более адаптивной.

3. Рассмотрение нескольких состояний: по сравнению с простой стратегией отслеживания тенденций, эта стратегия учитывает три состояния рынка (вверх, вниз, поперечно), что позволяет более полно понять динамику рынка.

4. Управление рисками: стратегия включает в себя определенные механизмы управления рисками, которые помогают контролировать потенциальные потери, путем ликвидации позиций в положении поперечного диска.

5. Интерпретируемость: Несмотря на использование вероятностной модели, логика стратегии относительно проста и понятна, что позволяет трейдерам понять и адаптироваться.

Стратегический риск

1. Чувствительность к параметрам: эффективность стратегии сильно зависит от установленных параметров конверсионной вероятности. Неправильная настройка параметров может привести к ошибочным торговым сигналам.

2. Отсталость: Поскольку стратегия основана на оценке состояния по цене закрытия, может существовать определенная отсталость, которая может пропустить важные переломные моменты в быстро меняющихся рынках.

3. Слишком большое упрощение: хотя модель Марковской цепочки позволяет зафиксировать некоторые рыночные динамики, она все же является упрощением сложных финансовых рынков и может игнорировать некоторые важные рыночные факторы.

4. Частые сделки: в зависимости от частого изменения состояния, стратегия может генерировать слишком много торговых сигналов, увеличивая стоимость сделки.

5. Рыночная адаптивность: в некоторых рыночных условиях (например, в долгосрочных трендовых рынках или в рынках с высокой волатильностью) стратегия может не работать.

Направление оптимизации стратегии

1. Введение большего количества состояний: можно рассмотреть возможность введения большего количества состояний рынка, таких как сильные и слабые, чтобы более точно изобразить динамику рынка.

2. Вероятность динамической корректировки: можно разработать механизм, который динамически корректирует вероятность конверсии в зависимости от недавнего рыночного поведения, чтобы сделать стратегию более адаптивной.

3. Интеграция с другими техническими показателями: можно интегрировать традиционные технические показатели, такие как скользящие средние и RSI, в логику оценки состояния, повышая точность прогноза.

4. Логика оценки состояния: можно использовать более сложную логику для оценки состояния рынка, например, учитывая изменения цены за несколько временных периодов.

5. Внедрение стоп-стоп: включение в стратегию механизма стоп-стоп для дальнейшего контроля риска и блокировки прибыли.

6. Отзыв и оптимизация параметров: проведение крупномасштабных отзывов о стратегии, оптимизация параметров вероятности конверсии с использованием методов, таких как генетические алгоритмы.

7. Учитывайте расходы на транзакции: учитывайте расходы на транзакции в логике стратегии, чтобы избежать чрезмерной частоты транзакций.

Подвести итог

Стратегия количественного трейдинга с вероятностным преобразованием состояния Марковской цепи - это инновационный метод трейдинга, который искусно сочетает вероятностные модели с традиционным техническим анализом. Посредством моделирования процесса преобразования состояния рынка, стратегия способна одновременно улавливать рыночные тенденции, учитывая рыночную случайность и неопределенность.

Несмотря на риски, связанные с чувствительностью к параметрам и возможным чрезмерным упрощением, его гибкость и интерпретируемость делают его потенциальным инструментом торговли. С дальнейшей оптимизацией, такой как введение большего количества состояний, динамической вероятности корректировки, интеграции других технических показателей, стратегия может лучше работать в реальных сделках.

Для трейдеров эта стратегия дает новые идеи о том, как использовать вероятностные модели для понимания и прогнозирования рыночных действий. Однако в практическом применении все еще требуется осторожность, а также полное отсчет и оценка риска, а также соответствующая корректировка в зависимости от конкретных торговых видов и рыночных условий.