اس مضمون میں ، ہم اورنسٹین-اوہلنبیک کے عمل کا جائزہ لیں گے ، اس کے ریاضیاتی فارمولے کی وضاحت کریں گے ، اس کو پیتھون کے ساتھ لاگو کریں گے اور اس کی نقالی کریں گے ، اور مقداری مالیاتی اور سسٹم ٹریڈنگ میں کچھ عملی ایپلی کیشنز پر تبادلہ خیال کریں گے۔ ہم ایک اعلی درجے کے بے ترتیب عمل کے ماڈل ، جسے اورنسٹین-اوہلنبیک (OU) عمل کہا جاتا ہے ، کا استعمال کریں گے ، جس کا استعمال واپسی ٹائم سیریز کو ماڈل کرنے کے لئے کیا جاسکتا ہے جو مساوات کی واپسی کا مظاہرہ کرتا ہے۔ یہ خاص طور پر مشتق قیمتوں میں سود کی شرح ماڈلنگ اور جب تجارت کی جاتی ہے تو سسٹم ٹریڈنگ کے لئے الگورتھم کے لئے مفید ہے۔

اورنسٹین-اولنبیک عمل کیا ہے؟

اورنسٹین-اولنبیک عمل ایک مسلسل وقت بے ترتیب عمل ہے جس کا استعمال اوسط قیمت کی واپسی کے عمل کو ماڈلنگ کرنے کے لئے کیا جاتا ہے۔ اس کا مطلب یہ ہے کہ معیاری بے ترتیب گھومنے یا براؤن کی نقل و حرکت کے برعکس جو لامحدود طور پر ڈرفٹ ہوسکتی ہے ، OU عمل اکثر وقت کے ساتھ ساتھ طویل مدتی اوسط پر واپس آجاتا ہے۔ ریاضی کے لحاظ سے ، OU عمل اس خاص طور پر بے ترتیب تفریحی مساوات (SDE) کا حل ہے جو اس اوسط قیمت کی واپسی کے عمل کو کنٹرول کرتا ہے۔ OU عمل کا SDE مندرجہ ذیل فارمولا کے ذریعہ دیا گیا ہے:

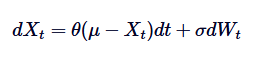
اس میں Xt وقت t پر بے ترتیب عمل کی نمائندگی کرتا ہے، μ طویل مدتی اوسط ہے، θ اوسط ریٹرن ریٹرن ہے،δ اتار چڑھاؤ ہے، اور DWt ویانر عمل یا معیاری براؤن تحریک ہے۔

تاریخی پس منظر اور اطلاق

اورنسٹین-اُلنبیک عمل کو ابتدائی طور پر 1930 میں لیونارڈ اورنسٹین اور جارج یوجین اُلنبیک نے اس مقصد کے لیے تجویز کیا تھا کہ وہ پارٹیکلز کی رفتار کو ماڈل کریں جو کشش کے ساتھ براؤن تحریک میں ہیں۔ وقت گزرنے کے ساتھ ساتھ اس کی افادیت فزکس سے کہیں زیادہ پھیل گئی ہے اور اس کا اطلاق حیاتیات، کیمسٹری، معاشیات اور فنانس جیسے مختلف شعبوں میں ہوتا ہے۔

کوانٹم فنانس میں ، OU عمل خاص طور پر اس رجحان کی ماڈلنگ کے لئے مفید ہے جس میں اوسط قیمت کی واپسی کا مظاہرہ کیا جاتا ہے۔ اس کی نمایاں مثالوں میں سود کی شرح ، زر مبادلہ کی شرح اور مالیاتی منڈیوں کی اتار چڑھاؤ شامل ہیں۔ مثال کے طور پر ، مقبول شرح سود کا ماڈل ، واسکک ماڈل ، OU عمل سے براہ راست اخذ کیا گیا ہے۔

کوانٹم فنانس میں اہمیت

اورنسٹین-اُلنبیک عمل کوئنٹی فنانس میں اہم ہے کیونکہ: اس کی میڈین ریگریشن کی نوعیت اس کو مالیاتی متغیرات کے ماڈلنگ کے لیے قدرتی انتخاب بناتی ہے جو بے ترتیب گھومنے کی بجائے مستحکم طویل مدتی میڈین کے ارد گرد اتار چڑھاؤ کا مظاہرہ کرتے ہیں۔ یہ خصوصیت شرح سود کے ماڈلنگ کے لیے اہم ہے، جہاں میڈین ریگریشن مرکزی بینک کے طویل مدتی مستحکم شرح سود کے اثرات کی عکاسی کرتی ہے۔

اس کے علاوہ ، OU عمل کو اثاثوں کی قیمتوں کا تعین کرنے والے ماڈل (بشمول مشتقات کی قیمتوں کا تعین) اور خطرے کے انتظام کی حکمت عملی میں بھی استعمال کیا جاتا ہے۔ یہ زیادہ پیچیدہ ماڈلز کے لئے تعمیراتی بلاکس کے طور پر بھی کام کرسکتا ہے ، مثال کے طور پر ، کاکس-انگرسول-روس (CIR) ماڈل ، جو OU عمل کو غیر منفی قیمت والی شرح سود کے ماڈلنگ کے لئے بڑھا دیتا ہے۔

اہم خصوصیات اور حواس

Ornstein-Uhlenbeck عمل کی اہم خصوصیات کا خلاصہ اس طرح کیا جا سکتا ہے:

• اوسط واپسی:OU عمل طویل مدتی اوسط پر واپس جانے کا رجحان رکھتا ہے۔ یہ براؤن کی نقل و حرکت جیسے عمل کے برعکس ہے ، جس میں اس رجحان کا مظاہرہ نہیں کیا گیا ہے۔
• عدم استحکامپیرامیٹرδ کنٹرول کے عمل میں بے ترتیب یا اتار چڑھاؤ کی سطح ≠ جتنا زیادہ اتار چڑھاؤ ہوتا ہے ، اس سے پہلے کہ اس عمل کو واپس آنے سے پہلے اوسط سے زیادہ انحراف ہوتا ہے ≠
• واپسی کی رفتار:پیرامیٹر θ عمل کی واپسی کی اوسط کی رفتار کا تعین کرتا ہے۔ θ قدر جتنی زیادہ ہوگی ، واپسی کی اوسط کی رفتار اتنی ہی تیز ہوگی۔
• استحکام:OU عمل ہموار ہے، جس کا مطلب یہ ہے کہ اس کی شماریاتی خصوصیات وقت کے ساتھ تبدیل نہیں ہوتی ہیں۔ یہ مالیاتی شعبے میں مستحکم نظام کی ماڈلنگ کے لئے ضروری ہے۔

بصری طور پر ، آپ اورنسٹین-اولنبیک کے عمل کو اوسط کے ارد گرد کھینچنے والی گٹھیا کے طرز عمل کی ماڈلنگ کے طور پر دیکھ سکتے ہیں۔ اگرچہ یہ عمل بے ترتیب اتار چڑھاؤ کی وجہ سے اوسط سے ہٹ سکتا ہے ، لیکن گٹھیا کے کھینچنے والی گٹھیا ((اوسط کی واپسی کی طرح) اس بات کو یقینی بناتا ہے کہ یہ آخر میں اوسط پر واپس آجائے گا۔

دیگر بے ترتیب عمل کے مقابلے میں

چونکہ OU عمل مختلف مالیاتی مظاہر کی ماڈلنگ کے ساتھ قریب سے وابستہ ہے ، لہذا اس کا اکثر دوسرے بے ترتیب عملوں (جیسے براؤن تحریک اور جیومیٹرک براؤن تحریک (GBM)) کے ساتھ موازنہ کیا جاتا ہے۔ براؤن کی نقل و حرکت کے برعکس (براؤن کی نقل و حرکت میں واپسی کی اوسط قیمت کا رجحان نہیں ہے) ، OU عمل میں نمایاں اوسط واپسی کا عمل ہے۔ اس سے یہ متغیرات کے ارد گرد مستحکم متوازن اتار چڑھاو کے منظر نامے کی ماڈلنگ کے لئے موزوں ہے۔

عام طور پر اسٹاک کی قیمتوں کا ماڈلنگ کرنے کے لئے استعمال ہونے والے جی بی ایم کے مقابلے میں اور اس میں بہاؤ اور اتار چڑھاؤ کے عناصر شامل ہیں ، او یو عمل میں اشاریہ نمو نہیں دکھائی دیتی ہے ، بلکہ اس کی اوسط قیمت کے گرد اتار چڑھاؤ ہوتا ہے۔ جی بی ایم وقت کے ساتھ بڑھتی ہوئی تعداد کے ماڈلنگ کے لئے زیادہ موزوں ہے ، جبکہ او یو عمل متغیرات کے ماڈلنگ کے لئے بہترین موزوں ہے جو اوسط قیمت کی واپسی کی خصوصیات کو ظاہر کرتا ہے۔

کوانٹم فنانس کی مثالیں

Ornstein-Uhlenbec عمل مالیاتی شعبے میں وسیع پیمانے پر استعمال ہوتا ہے ، خاص طور پر ماڈلنگ کے منظرناموں میں جہاں اوسط قدر کی واپسی ایک اہم خصوصیت ہے۔ ذیل میں ، ہم کچھ عام استعمال کے معاملات پر تبادلہ خیال کریں گے۔

شرح سود ماڈلنگ

OU عمل کا ایک نمایاں اطلاق شرح سود کی ماڈلنگ کے لئے ہے ، خاص طور پر واسکک ماڈل کے فریم ورک میں۔ واسکک ماڈل فرض کرتا ہے کہ شرح سود OU عمل کی پیروی کرتی ہے ، یعنی وقت کے ساتھ ساتھ شرح سود طویل مدتی اوسط پر واپس آجاتی ہے۔ یہ خصوصیت شرح سود کے طرز عمل کو درست طریقے سے ماڈل کرنے کے لئے ضروری ہے ، کیونکہ شرح سود لامحدود طور پر نہیں ہلتی ہے ، بلکہ معاشی حالات سے متاثر ہونے والی اوسط سطح کے قریب ہلتی ہے۔

اثاثوں کی قیمتوں کا تعین

اثاثوں کی قیمتوں میں ، خاص طور پر مقررہ آمدنی والی سیکیورٹیز میں ، OU عمل عام طور پر بانڈ کی واپسی کی شرح کے ارتقاء کی مشابہت کے لئے استعمال کیا جاتا ہے۔ OU عمل کی اوسط واپسی کی نوعیت اس بات کو یقینی بناتی ہے کہ واپسی کی شرح اس کی تاریخی اوسط سے زیادہ دور نہیں ہوگی ، جو کہ مشاہدہ شدہ مارکیٹ کے طرز عمل کے مطابق ہے۔ اس سے OU عمل بانڈ اور دیگر شرح سود حساس آلات کی قیمتوں کا تعین کرنے کے لئے ایک قیمتی آلہ بن جاتا ہے۔

جوڑی ٹریڈنگ حکمت عملی

جوڑی ٹریڈنگ ایک مارکیٹ غیر جانبدار حکمت عملی ہے جس میں دو متعلقہ اثاثوں میں آفسیٹ پوزیشن قائم کرنا شامل ہے۔ اس معاملے میں ، OU عمل خاص طور پر مفید ہے کیونکہ یہ دو اثاثوں کے مابین قیمت کے فرق کی ماڈلنگ کرسکتا ہے ، اور یہ فرق عام طور پر اوسط واپسی ہے۔ OU عمل کا استعمال کرتے ہوئے قیمت کے فرق کی ماڈلنگ کے ذریعہ ، تاجر منافع بخش اندراج اور باہر نکلنے کی تصدیق کرسکتا ہے جب قیمت اس کی اوسط سے ہٹ جاتی ہے ، اور اوسط واپسی کی پیش گوئی کرتا ہے ، اور اس طرح تجارتی سگنل تیار کرتا ہے۔

مثال کے طور پر ، اگر دو فیوچر کے مابین قیمت کا فرق کسی حد سے تجاوز کرنے تک پھیل جاتا ہے تو ، تاجر بہترین کارکردگی کا مظاہرہ کرنے والے فیوچر کو کالعدم کردیں گے اور خراب کارکردگی کا مظاہرہ کرنے والے فیوچر کو زیادہ کردیں گے ، امید ہے کہ قیمت کا فرق اپنی تاریخی اوسط سطح پر واپس آجائے گا ، اور اس طرح واپسی کی صورت میں منافع کمائے گا۔

Ornstein-Uhlenbeck SDE کا حل

اورنسٹین-اوہلنبیک کے عمل کے لئے تفریقی مساوات کی فارمولا اس کے حل کی بنیاد ہے۔ اس ایس ڈی ای کو حل کرنے کے لئے ہم نے انٹیگریٹڈ فیکٹرنگ کا استعمال کیا ہے۔ آئیے ایس ڈی ای کو دوبارہ لکھیں:

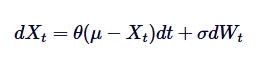
سب سے پہلے ، ہم دونوں اطراف کو 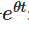کے انٹیگریٹڈ فیکٹر سے ضرب دیتے ہیں:

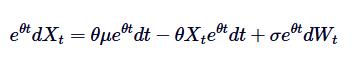
براہ کرم نوٹ کریں کہ اگر ہم 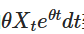کو دونوں اطراف میں شامل کریں تو بائیں طرف کو ضرب کے فرق کے طور پر ظاہر کیا جاسکتا ہے:

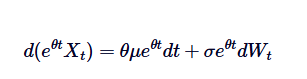
ہم 0 سے t تک دونوں اطراف کو بڑھا کر حاصل کرتے ہیں:

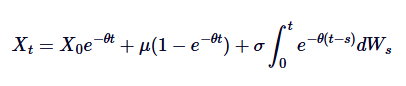
یہ اورنسٹین-اوہلنبیک ایس ڈی ای کا عمومی جواب ہے۔

مندرجہ بالا نکات کے واضح حل کے کئی اہم معنی ہیں۔ پہلا / اپ لوڈ / اثاثہ / 28e1d566f8ac15287edf3.png ابتدائی قدر کا وقت کے ساتھ ساتھ زوال ظاہر کرتا ہے ، جس سے ظاہر ہوتا ہے کہ عمل کس طرح آہستہ آہستہ بھول جاتا ہے۔ دوسرا / اپ لوڈ / اثاثہ / 28df8a8a50df8d8362d7c.png ظاہر کرتا ہے کہ عمل وقت کے ساتھ ساتھ اوسط قدر کی طرف بڑھتا ہے۔ تیسرا عنصر بے ترتیب کو متعارف کراتا ہے ، جس میں ویانر کے عمل کی انٹیگریشن بے ترتیب اتار چڑھاؤ کی وضاحت کرتی ہے۔

اس حل میں یقین کی اوسط واپسی کے عمل اور براؤن تحریک سے چلنے والے بے ترتیب اجزاء کے مابین توازن پر زور دیا گیا ہے۔ اس حل کو سمجھنا OU کے عمل کو مؤثر طریقے سے ماڈل کرنے کے لئے ضروری ہے ، جیسا کہ ذیل میں بیان کیا گیا ہے۔

دوسرے بے ترتیب عمل کے ساتھ روابط

Ornstein-Uhlenbeck عمل دوسرے مشہور بے ترتیب عملوں (بشمول براؤن تحریک اور واسکک ماڈل) کے ساتھ کئی اہم روابط ہیں۔

براؤن تحریک کے ساتھ تعلقات

اورنسٹین-اوہلنبیک عمل کو براؤن کی تحریک کا میڈین ریٹرن ورژن سمجھا جاسکتا ہے۔ براؤن کی تحریک ایک ایسے عمل کی وضاحت کرتی ہے جس میں آزاد اضافے کے ساتھ رجحان ہوتا ہے اور اس میں کوئی میڈین ریٹرن نہیں ہوتا ہے ، جبکہ OU عمل براؤن کی تحریک کو ڈرفٹ کی اصطلاحات کو تبدیل کرکے میڈین ریٹرن متعارف کراتا ہے ، جس سے عمل کو مرکزی قدر میں واپس لایا جاتا ہے۔ ریاضیاتی طور پر ، اگر ہم اس کی ترتیب دیں توθ = 0 ، OU عمل کو معیاری براؤن کی تحریک میں کم کیا جائے گا جس میں لہر لگی ہوئی ہے:

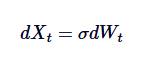
اس طرح، براؤن کی تحریک OU عمل کی ایک خاص مثال ہے، جس میں اوسط واپسی کی غیر موجودگی کے مطابق ہے.

واسکک ماڈل کے ساتھ تعلقات

Vasicek ماڈل وسیع پیمانے پر شرح سود ماڈلنگ کے لئے استعمال کیا جاتا ہے، بنیادی طور پر شرح سود کے ارتقاء میں Ornstein-Uhlenbeck عمل کا اطلاق. Vasicek ماڈل فرض کرتا ہے کہ شرح سود OU عمل کی پیروی کرتی ہے، جہاں SDE کی تعریف کی جاتی ہے:

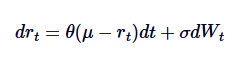
اس میں ، rt مختصر مدت کے سود کی شرح کی نمائندگی کرتا ہے ، پیرامیٹرز θ ، μ اورδ کی تشریح OU کے عمل میں کی جانے والی تشریح سے ملتی جلتی ہے۔ واسکک ماڈل سود کی شرح کے راستے میں اوسط واپسی پیدا کرنے کے قابل ہے ، جو مالی ماڈلنگ میں اس کے اہم فوائد میں سے ایک ہے۔

ان تعلقات کو سمجھنے سے یہ سمجھنے میں مدد ملتی ہے کہ OU عمل مختلف ماحول میں کس طرح استعمال ہوتا ہے ، خاص طور پر مالیاتی شعبے میں۔ ہم ذیل میں استعمال کی مثالوں پر تبادلہ خیال کرتے ہوئے ان روابط کے عملی معنی پر غور کریں گے۔

Ornstein-Uhlenbeck پروسیس کو پیتھون کے ساتھ ماڈل کریں

اس سیکشن میں ، ہم بات کریں گے کہ پیتھون کا استعمال کرتے ہوئے اورنسٹین-اوہلنبیک ((OU) عمل کو کیسے ماڈل کیا جائے۔ اس میں OU عمل کی وضاحت کرنے والے بے ترتیب مائکرو ڈفریجریشن مساوات (SDE) کو الگ تھلگ کرنے کے لئے Euler-Maruyama کی علیحدگی کا استعمال کرنا شامل ہے۔

ایس ڈی ای کی تقسیم

آئیے ایس ڈی ای کے ریاضی کے فارمولے پر ایک نظر ڈالیں اور ہر اصطلاح کا خلاصہ کریں:

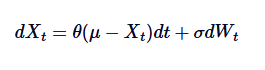
میں

• Xt وقت t پر عمل کی قیمت ہے
• θ میڈین ویلیو ریگریشن کی رفتار ہے۔
• μ عمل کی طویل مدتی اوسط ہے۔
• δ اتار چڑھاؤ کی شرح پیرامیٹرز ہے.
• dWt ویانر پروسیس ((معیاری براؤن تحریک) کا اضافہ ظاہر کرتا ہے۔

اس عمل کو کمپیوٹر پر ماڈل کرنے کے لیے ہمیں مسلسل وقت SDE کو ڈسچارج کرنے کی ضرورت ہے۔ ایک عام طریقہ Euler-Maruyama ڈسچارج کرنا ہے، جو کہ چھوٹے ڈسچارج وقت کے قدموں کی لمبائی کو مدنظر رکھتے ہوئے مسلسل عمل کو قریب تر کرتا ہے۔ اورنسٹین-Uhlenbeck عمل کی ڈسچارج شکل مندرجہ ذیل سے دی گئی ہے:

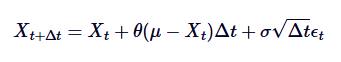
ان میں 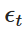ایک بے ترتیب متغیر ہے جو معیاری عمودی تقسیم سے نکالا گیا ہے (یعنی 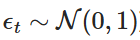) ۔ اس انضمام نے ہمیں وقت کے ساتھ ساتھ Xt کی قدر کا حساب لگانے کی اجازت دی ہے ، اس طرح OU عمل کے طرز عمل کی نقالی ہوتی ہے۔

پیتھون کا نفاذ

اب ہم پیتھون کے ساتھ Ornstein-Uhlenbeck عمل کو لاگو کرتے ہیں.

سب سے پہلے ہم NumPy اور Matplotlib کو معیاری انداز میں درآمد کرتے ہیں۔ اس کے بعد ہم OU ماڈل کے لئے تمام پیرامیٹرز کی وضاحت کرتے ہیں۔ اس کے بعد ، ہم پہلے سے N لمبائی کا ایک NumPy صف تفویض کرتے ہیں تاکہ OU کا راستہ حساب کرنے کے بعد اس میں شامل کیا جاسکے۔ پھر ہم N-1 کو تکرار کرتے ہیں (مرحلہ 1 میں ابتدائی شرط X0 دی گئی ہے) ، بے ترتیب اضافے کا ڈبلیو ڈبلیو ماڈل کرتے ہیں ، اور پھر OU کے راستے کی اگلی تکرار کو مندرجہ بالا ریاضی کے فارمولے کے مطابق شمار کرتے ہیں۔ آخر میں ، Matplotlib کا استعمال کرتے ہوئے راستے کی تاریخ کا نقشہ بنائیں۔

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

نقشے کے نتائج مندرجہ ذیل ہیں:

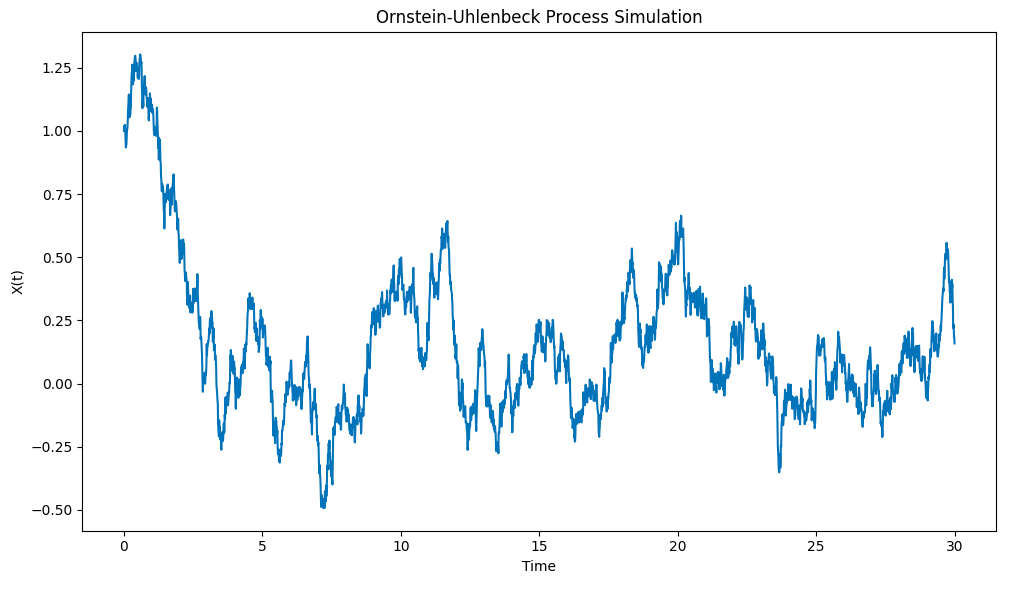
پیتھون کے ساتھ Ornstein-Uhlenbeck عمل کی نقالی

نوٹ کریں کہ یہ عمل کس طرح ابتدائی حالات سے X0 = 1 تک اوسط μ = 0 تک تیزی سے کھینچتا ہے ، اور پھر جب یہ اس اوسط سے ہٹ جاتا ہے تو ، یہ اس اوسط پر واپس آنے کا رجحان ظاہر کرتا ہے۔

خلاصہ اور بعد کے اقدامات

اس مضمون میں ، ہم نے اورنسٹین-اوہلنبیک کے عمل کا جائزہ لیا ، اس کے ریاضیاتی فارمولے کی وضاحت کی ، اور پیتھون کا ایک بنیادی نفاذ فراہم کیا جس میں مستقل وقت SDE کے الگ الگ ورژن کی نقالی کی گئی تھی۔ اس کے بعد کے مضامین میں ، ہم OU عمل پر مبنی زیادہ پیچیدہ SDE کی تحقیقات کریں گے اور دیکھیں گے کہ ان کو سسٹم ٹریڈنگ اور مشتق قیمتوں کا تعین کرنے والی ایپلی کیشنز میں کس طرح استعمال کیا جاسکتا ہے۔

مکمل کوڈ

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

اصل مقالے کا لنک: https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/