کیلی فارمولا - پوزیشن کنٹرول کے لیے ایک طاقتور ٹول

** فرض کریں کہ آپ کے جیتنے کا امکان 60٪ ہے اور آپ کے ہارنے کا امکان 40٪ ہے۔ جب آپ جیتتے ہیں تو آپ کی خالص منافع کی شرح 100٪ ہے اور جب آپ ہار جاتے ہیں تو آپ کا نقصان 100٪ ہے۔ یعنی ، اگر آپ جیت جاتے ہیں تو ، آپ ہر 1 ڈالر جیت سکتے ہیں ، اور اگر آپ ہار جاتے ہیں تو ، آپ ہر 1 ڈالر کھو دیں گے۔

• 1، اس سلاٹ کے لئے، ہر شرط پر متوقع واپسی 60 فیصد ہے.*1-40%*1 = 20٪، امید کی واپسی مثبت ہے۔ یعنی یہ ایک ایسا تعطل ہے جس میں ڈاکوؤں کا فائدہ ہے ، اور اس میں بہت بڑا فائدہ ہے۔

تو پھر ہم کس طرح شرط لگائیں؟

اگر ہم سنجیدگی سے غور نہ کریں تو ہم سوچیں گے کہ چونکہ میں ہر شرط پر 20 فیصد منافع کی توقع کرتا ہوں تو مجھے زیادہ سے زیادہ منافع حاصل کرنے کے لئے ہر شرط پر زیادہ سے زیادہ رقم لگانا چاہئے۔ اس تناسب کی زیادہ سے زیادہ قیمت 100 فیصد ہے۔

لیکن بظاہر ہر کھیل میں 100 فیصد سرمایہ لگانا غیر معقول ہے ، کیونکہ ایک بار جب کوئی کھیل ہار جاتا ہے تو ، تمام سرمایہ ختم ہوجاتا ہے ، اگلے کھیل میں حصہ نہیں لے سکتا ، صرف خاموشی سے باہر نکل سکتا ہے۔ اور طویل عرصے سے ، ایک بار ہارنے والا یہ واقعہ ناگزیر ہے ، لہذا طویل عرصے سے یہ یقینی طور پر دیوالیہ ہوجائے گا۔

تو اس سے یہ نتیجہ اخذ کیا جاتا ہے کہ جب تک کہ ایک بیعانہ کی صورت میں ایک ہی وقت میں اس کی پوری رقم ضائع ہونے کا امکان موجود ہے ، چاہے یہ بہت چھوٹا ہو ، تو اس کی پوزیشن کبھی بھی پوری نہیں ہوگی۔ کیونکہ طویل عرصے میں، چھوٹا امکان واقعہ ضرور ہوتا ہے، اور حقیقی زندگی میں، چھوٹا امکان واقعہ کے واقعے کی اصل امکان اس کے نظریاتی امکان سے کہیں زیادہ ہے. یہ فنانس میں چربی کے اثر ہے.

• 2۔ پھر سے تعطل کی طرف لوٹتے ہیں۔ اگر ہر بار 100 فیصد شرط لگانا غیر معقول ہے تو پھر 99 فیصد شرط لگانا کیسا؟ اگر ہر بار 99 فیصد شرط لگائی جائے تو نہ صرف یہ ضمانت دی جاسکتی ہے کہ آپ کبھی دیوالیہ نہیں ہوں گے ، بلکہ اگر آپ خوش قسمت ہیں تو آپ کو بہت زیادہ منافع مل سکتا ہے۔

کیا یہ حقیقت ہے؟

ہم اس مسئلے کا نظریاتی طور پر تجزیہ نہیں کریں گے، ہم ایک تجربہ کر سکتے ہیں۔ ہم اس تعطل کا مشاہدہ کریں گے، اور ہر بار 99 فیصد شرط لگائیں گے، اور دیکھیں گے کہ کیا ہوتا ہے۔

اس تجربے کو ایکسل میں کیا جا سکتا ہے۔ ذیل میں تصویر ملاحظہ کریں:

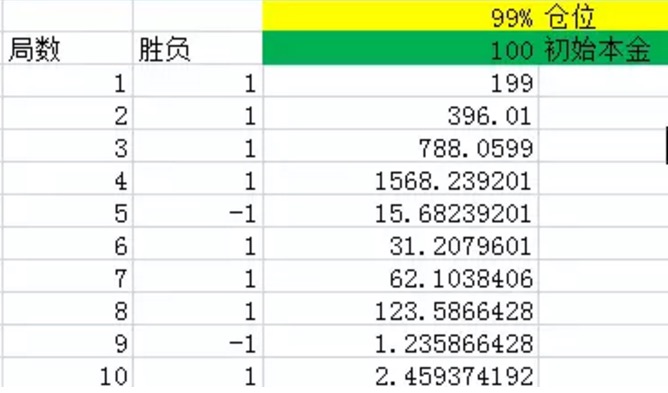تصویر 1

جیسا کہ اوپر کی تصویر میں دکھایا گیا ہے ، پہلا کالم اسٹیج کی تعداد کو ظاہر کرتا ہے۔ دوسرا کالم جیتنے کے لئے ہے ، اور ایکسل 60٪ امکان کے مطابق 1 پیدا کرے گا ، یعنی 60٪ امکان خالص منافع 1 ، 40٪ امکان خالص منافع -1 پیدا کرے گا۔ تیسرا کالم ہر اسٹیج کے اختتام پر تمام فنڈز کو نشان زد کرتا ہے۔ اس تجربے میں ہر شرط کی پوزیشن 99٪ ہے ، اور ابتدائی سرمایہ 100 ہے ، جو زرد اور سبز رنگ میں ہے۔

جیسا کہ آپ اس گراف سے دیکھ سکتے ہیں ، 10 کھیلوں کے بعد ، 10 کھیلوں میں جیتنے کے امکانات 8 ہیں ، جو 60٪ سے زیادہ ہیں ، اور صرف دو بار ہار گئے ہیں۔ لیکن اس کے باوجود ، آخری رقم صرف 2.46 ڈالر رہ گئی ، جو بنیادی طور پر ضائع ہوگئی ہے۔

اور جب میں اس کو بڑھاتا ہوں، ایک ہزار، دو ہزار، تین ہزار… تو آپ دیکھ سکتے ہیں کہ آخر میں، آپ کے پاس جو پیسہ ہے وہ بنیادی طور پر صفر کی طرف جاتا ہے۔

اور چونکہ یہ 99 فیصد بھی کام نہیں کرتا ہے، تو آئیے ہم کچھ دوسرے تناسب کے ساتھ کوشش کریں، جیسا کہ ذیل میں دکھایا گیا ہے: اس سے ظاہر ہوتا ہے کہ جب پوزیشن کو 99 فیصد سے کم کیا جاتا ہے، تو 90 فیصد، 80 فیصد، 70 فیصد، 60 فیصد، اور اسی طرح کے 10 کھیلوں کے نتائج بالکل مختلف ہوتے ہیں. اس سے ظاہر ہوتا ہے کہ پوزیشنوں میں کمی کے ساتھ، 10 کھیلوں کے بعد فنڈز میں اضافہ ہوتا ہے.

اگر آپ یہاں دیکھتے ہیں تو آپ کو پتہ چل جائے گا کہ یہ مسئلہ اتنا سادہ نہیں ہے۔ یہاں تک کہ اگر یہ ایک بہت بڑا سودا ہے جس میں جعلی کھلاڑیوں کا غلبہ ہے ، تو یہ بھی نہیں ہے کہ ہر وقت جیت لیا جائے گا۔

تو ، طویل مدتی منافع کو زیادہ سے زیادہ کرنے کے لئے کس طرح شرط لگائیں؟

کیا اس کا مطلب یہ ہے کہ اس کا تناسب جتنا کم ہو گا اتنا ہی بہتر ہو گا جیسا کہ اوپر دکھایا گیا ہے؟

تو پھر یہ بہترین تناسب کیا ہے؟

کیا آپ کو لگتا ہے کہ آپ کیلی فارمولے کے ذریعے اس مسئلے کا حل تلاش کر سکتے ہیں؟

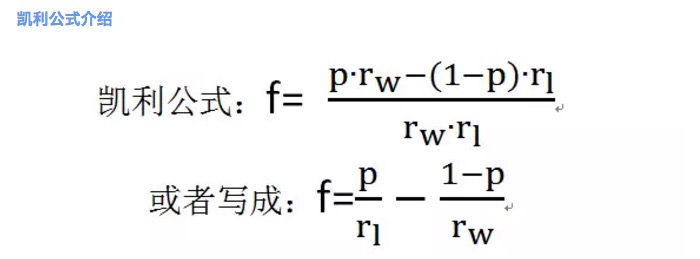تصویر 2

جہاں f بہترین شرط کا تناسب ہو۔ p جیتنے کا امکان ہے۔ rw جیتنے پر خالص واپسی کی شرح ہے۔ مثال کے طور پر ، 1 میں rw = 1۔ rl ہارنے پر خالص نقصان کی شرح ہے۔ مثال کے طور پر ، 1 میں rl = 1۔ نوٹ کریں کہ یہاں rl> 0 ہے۔

کیلی فارمولے کے مطابق، یہ حساب لگایا جا سکتا ہے کہ باکس 1 میں سب سے زیادہ شرط کا تناسب 20 فیصد ہے۔

ہم اس نتیجے کو سمجھنے کے لئے کچھ تجربات کر سکتے ہیں۔

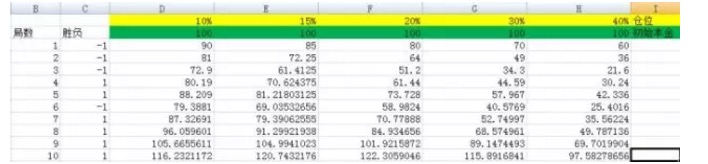تصویر نمبر 3

جیسا کہ تصویر میں دکھایا گیا ہے ، ہم نے پوزیشن کو 10٪ ، 15٪ ، 20٪ ، 30٪ ، 40٪ مقرر کیا ہے۔ ان کے مطابق کالموں کی تعداد بالترتیب D ، E ، F ، G ، H ہے۔

اور جب میں نے یہ تجربہ 3000 بار کیا تو میں نے محسوس کیا کہ میں نے اپنے آپ کو ایک ہی جگہ پر پایا۔ اور جب میں نے یہ تجربہ پانچ ہزار بار کیا تو میں نے محسوس کیا کہ میں نے ایک ہزار بار یہ تجربہ کیا ہے۔ اس سے آپ دیکھ سکتے ہیں کہ F کالم کے مساوی نتائج سب سے زیادہ ہیں، اور دیگر کالموں کے مقابلے میں دباؤ جڑ ایک مقداری نہیں ہے۔ اور F کالم کے مساوی پوزیشن کا تناسب 20٪ ہے۔

کیلی فارمولے کی طاقت آپ کو نظر آرہی ہے۔ اوپر کے تجربے میں، اگر آپ نے بدقسمتی سے تناسب کو 40 فیصد منتخب کیا، یعنی H کالم، تو پھر 5000 گھماؤ کے بعد، آپ کا اصل پیسہ اگرچہ 100 سے 22799985.75 ہو گیا، بہت زیادہ منافع ہوا۔ لیکن 20 فیصد تناسب کے نتیجے کے مقابلے میں، یہ واقعی کوئی پیسہ نہیں جیتنے کے مترادف ہے۔

یہ علم کی طاقت ہے

• کیلی فارمولا کو سمجھنا

کیلی کے فارمولے کی ریاضیاتی استنباط اور اس کی پیچیدگی ، بہت اعلی اور گہری ریاضیاتی علم کی ضرورت ہے ، لہذا یہاں اس پر بحث کرنے کا کوئی فائدہ نہیں ہے۔ یہاں میں کچھ تجربات کے ذریعے کیلی کے فارمولے کے بارے میں آپ کی ذہنی تفہیم کو گہرا کروں گا۔

ہم ایک بار پھر ایک کھیل دیکھیں۔ کھیل 2: آپ کے ہارنے اور جیتنے کا امکان 50٪ ہے، مثال کے طور پر سکے پھینکنا۔ جیتنے پر خالص منافع کی شرح 1 ہے، یعنی rw = 1، اور ہارنے پر خالص نقصان کی شرح 0.5 ہے، یعنی rl = 0.5۔ یعنی جب آپ ہر ایک ڈالر جیتتے ہیں تو آپ 1 ڈالر جیت سکتے ہیں، اور جب آپ ہارتے ہیں تو آپ کو صرف 5 سین ادا کرنا پڑتا ہے۔

اس کے علاوہ ، یہ بھی واضح ہے کہ اسکرین شاٹ 2 میں 0.25 کی متوقع آمدنی ہے ، اور یہ ایک ایسا اسکرین شاٹ ہے جس میں ہیکرز کا بہت بڑا فائدہ ہے۔

کیلی فارمولے کے مطابق ، ہم ہر کھیل کے لئے بہترین بیٹنگ تناسب حاصل کرسکتے ہیں:

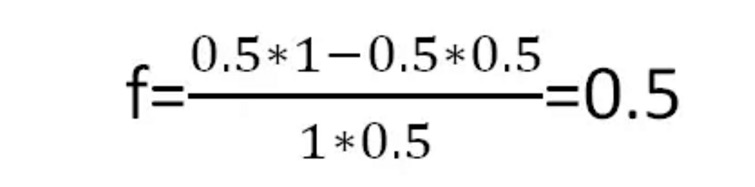تصویر 4

اس کا مطلب یہ ہے کہ ہر بار جب آپ آدھے پیسے کی شرط لگاتے ہیں تو ، آپ کو طویل مدتی میں زیادہ سے زیادہ منافع ملتا ہے۔

اور میں آپ کو بتاتا ہوں کہ آپ کے تجربے کے مطابق اوسط شرح نمو کا تصور کیا ہے۔

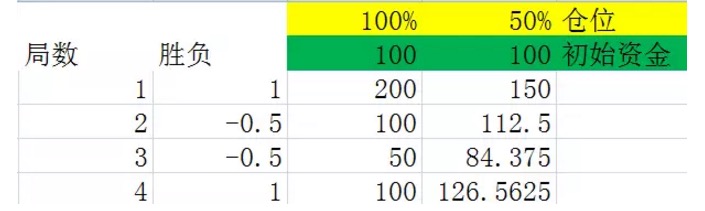
ہم نے تجربہ 2.1 کے ساتھ شروع کیا ہے، یہ دو تصاویر ہیں:

تصویر 5

یہ دونوں گرافس مشابہت لٹکن 2 کے تجربات ہیں، دوسرے کالم میں جیتنے والے کالم میں، تجربات کا 50٪ امکان پیدا ہوتا ہے 1، منافع 100٪ کا مطلب ہے ‬ 50٪ امکان پیدا ہوتا ہے -0.5، نقصان 50٪ کا مطلب ہے ‬ تیسرے اور چوتھے کالم میں پوزیشن 100٪ اور 50٪ کے تحت ہر لٹکن کے بعد اپنے پاس موجود رقم ‬

دونوں گرافوں کا محتاط موازنہ کرنے سے یہ نتیجہ اخذ کیا جاسکتا ہے کہ ایک ہی انگوٹی کی تعداد کے بعد ، حتمی نتیجہ صرف ان انگوٹیوں میں جیتنے والے انگوٹیوں کی تعداد اور ہارنے والے انگوٹیوں کی تعداد سے متعلق ہے ، اور ان انگوٹیوں میں جیتنے والے انگوٹیوں اور ہارنے والے انگوٹیوں کی ترتیب سے کوئی تعلق نہیں ہے۔ مثال کے طور پر ، پچھلے دو گرافوں میں بھی 4 انگوٹیوں کا انعقاد کیا گیا تھا ، اسی طرح ہر گراف میں دو جیتنے والے دو انگوٹیوں کو کھو دیا گیا تھا ، لیکن پہلے گراف کی ہار جیت کی جیت تھی ، اور دوسرے گراف کی ہار جیت کی جیت تھی۔ ان کے حتمی نتائج ایک جیسے ہیں۔

یقینا یہ نتیجہ بہت آسان ثابت ہوتا ہے (ضرب اور تبادلہ کا قانون ، ابتدائی طلباء کر سکتے ہیں) ، لیکن یہاں یہ ثابت نہیں ہوتا ہے ، مندرجہ بالا دو مثالیں آپ کو اچھی طرح سے سمجھنے کے لئے کافی ہیں۔

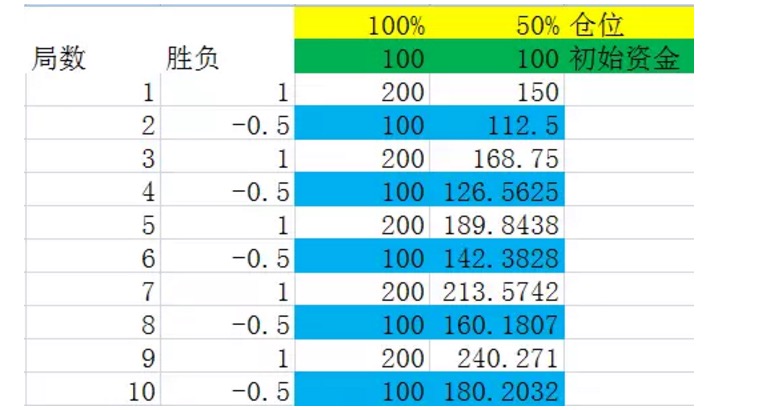
تو چونکہ حتمی نتیجہ جیت اور ہار کے تسلسل سے کوئی تعلق نہیں رکھتا، تو ہم فرض کرتے ہیں کہ سست 2 تجربے 2.2 کی طرح ہی چلتا ہے، جیسا کہ ذیل میں دکھایا گیا ہے:

تصویر 6

ہم فرض کرتے ہیں کہ جیت اور ہار کا تبادلہ ہوتا ہے ، کیونکہ نتیجہ 1 یہ ہے کہ طویل مدتی میں ، اس سے نتائج پر کوئی اثر نہیں پڑتا ہے۔

تصویر کو خود دیکھنے سے پہلے ہم ایک تعریف کرتے ہیں۔ فرض کریں کہ کچھ سلاخوں کو ایک مجموعہ کے طور پر سمجھا جائے ، جس میں مختلف نتائج کی فریکوئنسی اس کے امکانات کے برابر ہے ، اور اس مجموعہ کی سلاخوں کی تعداد سبھی کو پورا کرنے والے مجموعہ میں سلاخوں کی کم سے کم تعداد ہے ، تو ہم اس مجموعہ کو سلاخوں کا ایک مجموعہ کہتے ہیں۔ مثال کے طور پر اوپر دیئے گئے تجربے میں ، سلاخوں کا ایک مجموعہ دو سلاخوں کی سلاخوں کی نمائندگی کرتا ہے ، جس میں سے ایک جیت جاتا ہے اور ایک ہار جاتا ہے۔

مندرجہ بالا چارٹ میں نیلے رنگ کے نشان والے نمبروں کو قریب سے دیکھیں ، وہ ایک جمود کا اختتام ہیں۔ آپ دیکھیں گے کہ یہ نمبروں میں مستقل طور پر اضافہ ہوتا رہتا ہے۔ جب پوزیشن 100٪ ہے تو ، نیلے رنگ کے نشان والے نمبروں میں اضافہ کی شرح 0٪ ہے ، یعنی جمود کے ایک سیٹ کے بعد اصل رقم میں 0٪ اضافہ۔ یہ بھی اس بات کی وضاحت کرتا ہے کہ جب ہر بار پوزیشن بھر جاتی ہے تو ، جمود 2 میں درمیانی مدت میں منافع بخش نہیں ہوتا ہے۔ جب پوزیشن 50٪ ہے (یعنی کیلی فارمولے سے حاصل ہونے والا بہترین تناسب) ، تو نیلے رنگ کے نشان والے نمبروں میں اضافہ کی شرح 12.5٪ ہے ، یعنی جمود کے ایک سیٹ کے بعد اصل رقم میں 12.5٪ اضافہ ہوا ہے۔

یہ ایک عام قانون ہے کہ ہر بریک اپ کے بعد ترقی کی شرح پوزیشن سے متعلق ہے۔ اور ہر بریک اپ کے بعد ترقی کی شرح جتنی زیادہ ہوگی ، طویل مدتی میں حتمی منافع اتنا ہی زیادہ ہوگا۔

ہر جمود کے بڑھنے کی شرح کے مطابق ہر جمود کی اوسط شرح کا حساب لگایا جا سکتا ہے g. اوپر کے گراف میں، ہر جمود کے گروپ میں دو جمود شامل ہیں، تو ہر جمود کی اوسط شرح

تصویر 7

طویل مدت میں ، سرمایہ کو زیادہ سے زیادہ بڑھانا چاہتے ہیں ، دراصل صرف اس بات کو یقینی بنائیں کہ r زیادہ سے زیادہ ہو ، یعنی g کو زیادہ سے زیادہ کریں۔ اور بہترین شرط کا تناسب f دراصل max ((g) کے حل کی طرف سے بھی نکلا ہے۔

• کیلی فارمولہ کے دیگر نتائج

کیلی لیجنڈ

کیلی فارمولہ ابتدائی طور پر اے ٹی اینڈ ٹی بیل لیبارٹریز کے ماہر طبیعیات جان لیری کیلی کے لئے بنایا گیا تھا ، جو اپنے ساتھی کلاڈ ایرووڈ شینون کی طویل فاصلے پر ٹیلیفون لائنوں کے بارے میں تحقیق پر مبنی تھا۔ کیلی نے شینون کی معلوماتی نظریہ کو کس طرح لاگو کرنے کے بارے میں مسئلہ حل کیا جب ایک جواری کے پاس اندرونی معلومات ہوتی ہیں۔ جواری بہترین شرط لگانے کی رقم کا فیصلہ کرنا چاہتا ہے ، اور اس کی اندرونی معلومات کو کامل ہونے کی ضرورت نہیں ہے (کوئی خبر نہیں) ، یعنی اسے مفید فائدہ حاصل کرنے دیتا ہے۔ کیلی کا فارمولہ بعد میں شینون کے ایک اور ساتھی ایڈورڈ سوپ نے بیس پوائنٹس اور اسٹاک مارکیٹ میں لاگو کیا تھا۔ ساؤپ نے کام کے باقی حصوں کو استعمال کیا ، اور کئی مہینوں کے سخت حساب کتاب کے ذریعے ، ایک ریاضیاتی مقالہ لکھا جس کا عنوان تھا 21 پوائنٹ پر جیتنے کی ترجیحی حکمت عملی۔ انہوں نے اپنے علم کا استعمال کیا ، اور راتوں رات جیتنے والے نے نیواڈا رینو شہر کے تمام جوئے بازی کے اڈوں پر حملہ کیا ، اور کامیابی سے 21 پوائنٹ پر جیتنے والی میز سے دسیوں ہزار ڈالر جیت لئے۔ وہ امریکی وال اسٹریٹ کوانٹومیٹڈ ٹریڈنگ ہیج فنڈ کے باپ دادا بھی تھے۔ انہوں نے 70 کی دہائی میں پہلا کوانٹومیٹڈ ٹریڈنگ ہیج فنڈ بنایا تھا۔ 1962 میں شائع ہونے والے اس کے کالم نے جوکر کو شکست دی ، جو فنانس کی ایک کلاسیکی کتاب بن گئی۔

نقطہ نظر کا استعمال

کیلی فارمولے سے حقیقی زندگی میں پیسہ کیسے کمایا جائے؟ اس کا مطلب یہ ہے کہ ہم ایک ایسا جمود پیدا کر رہے ہیں جو کیلی فارمولے کی شرائط پر پورا اترتا ہے۔ میرے خیال میں یہ جمود مالیاتی منڈیوں سے ہی پیدا ہوتا ہے۔ میں نے حال ہی میں ٹریڈنگ سسٹم کے بارے میں تحقیق کی ہے کہ ایک اچھے ٹریڈنگ سسٹم کے لئے سب سے اہم کیا ہے؟ ایک مثبت منافع کی توقع کے ساتھ خرید و فروخت کا قاعدہ 10 فیصد اہمیت کا حامل ہے ، جبکہ ایک اچھا فنڈ کنٹرول کا طریقہ 40 فیصد اہمیت کا حامل ہے ، اور باقی 50 فیصد لوگوں کے نفسیاتی کنٹرول پر قابو پانے کا ہے۔ اور کیلی فارمولا میرے لئے ایک ایسا آلہ ہے جس سے میں اپنے پیسے کی پوزیشن پر قابو پا سکتا ہوں۔ مثال کے طور پر ، میں نے پہلے ایک اسٹاک ٹریڈنگ سسٹم کا مطالعہ کیا ، جو ہر ہفتے ایک تجارت کرتا ہے ، ہر ہفتے تجارت کی کامیابی کا امکان 0.8 ہے ، اور ناکامی کا امکان 0.2 ہے۔ جب کامیاب ہوتا ہے تو 3٪ کمائی کی جاسکتی ہے ((کمشن ، پرنٹ ٹیکس کٹوتی) ، اور ہر ناکامی پر 5٪ نقصان ہوتا ہے۔ کیلی فارمولا جاننے سے پہلے ، میں اندھا پنڈال ٹریڈنگ کر رہا تھا ، اور مجھے نہیں معلوم تھا کہ میری پوزیشن غلط ہے ، نفسیاتی طور پر بہت ہی غلط ہے۔ کیلی فارمولا کے استعمال کے بعد ، حساب کتاب کی بہترین پوزیشن 9.33 ہونی چاہئے ، یعنی اگر قرض کی شرح سود 0 ہے تو ، سب سے تیز رفتار سے زیادہ سرمایہ کاری کی شرح حاصل کرنے کے لئے لیوریجڈ ٹریڈنگ کا استعمال کرنا چاہئے ، اس فارمولے کے حساب سے ہر تجارت میں اوسطا شرح نمو r کے برابر ہے جو 7.44٪ ہے ، اور ہر تجارت میں اوسط سرمایہ کاری کی شرح نمو r کے برابر ہے۔ 1.35 ((یعنی اصل آمدنی کی توقع کی جاتی ہے۔) تجربے کے بعد ، میں بھی پتہ چلا کہ لیوریجڈ ٹریڈنگ یقینا کیلی فارمولا عملی استعمال میں اتنا آسان نہیں ہوسکتا ہے ، اور بہت سی مشکلات پر قابو پانے کی ضرورت ہے۔ مثال کے طور پر لیورڈ ایکسچینج کے لئے درکار فنڈز کی لاگت ، مثال کے طور پر حقیقت میں فنڈز لامحدود طور پر تقسیم نہیں ہوتے ہیں ، مثال کے طور پر مالیاتی منڈیوں میں اتنا آسان نہیں ہے جتنا اوپر ذکر کیا گیا ہے۔ لیکن اس کے باوجود ، کیلی فارمولا ہمیں آگے بڑھنے کا راستہ دکھاتا ہے۔