8 مشین لرننگ الگورتھم کا موازنہ
 0
0
 6825
6825
8 مشین لرننگ الگورتھم کا موازنہ
یہ مضمون بنیادی طور پر مندرجہ ذیل عام طور پر استعمال ہونے والے الگورتھم کے موافقت کے منظرناموں اور ان کے فوائد اور نقصانات کا جائزہ لے رہا ہے۔
مشین لرننگ کے بہت سے الگورتھم ہیں ، درجہ بندی ، رجعت ، گروپنگ ، سفارشات ، تصویری شناخت کے شعبوں میں ، اور اسی طرح کے ، مناسب الگورتھم تلاش کرنا واقعی آسان نہیں ہے ، لہذا عملی استعمال میں ، ہم عام طور پر ایلیویشن لرننگ کے طریقوں کو استعمال کرتے ہوئے تجربہ کرتے ہیں۔
عام طور پر شروع میں ہم عام طور پر تسلیم شدہ الگورتھم کا انتخاب کرتے ہیں ، جیسے ایس وی ایم ، جی بی ڈی ٹی ، اڈابوسٹ ، اور اب گہری سیکھنے میں بہت دلچسپی ہے ، نیورل نیٹ ورکس بھی ایک اچھا انتخاب ہیں۔
اگر آپ کو درستگی کی فکر ہے تو ، بہترین طریقہ یہ ہے کہ الگورتھم کو ایک ایک کرکے جانچیں ، موازنہ کریں ، اور پھر پیرامیٹرز کو ایڈجسٹ کریں تاکہ یہ یقینی بنایا جاسکے کہ ہر الگورتھم بہترین حل تک پہنچتا ہے ، اور آخر میں بہترین انتخاب کریں۔
لیکن اگر آپ کو صرف آپ کے مسئلے کو حل کرنے کے لئے کافی اچھا الگورتھم تلاش کر رہے ہیں، یا یہاں کچھ تجاویز ہیں، تو ذیل میں الگورتھم کے فوائد اور نقصانات کا تجزیہ کریں، جو الگورتھم کے فوائد اور نقصانات کی بنیاد پر، یہ آسان ہے کہ ہم اسے منتخب کریں.
- ## فرق اور فرق
اعداد و شمار میں، ایک ماڈل کی اچھی یا بری حالت کو اس کے انحرافات اور فرق سے ماپا جاتا ہے، تو آئیے پہلے ہم اس کے انحرافات اور فرق کو عام کریں:
انحراف: یہ پیش گوئی کی قیمت (یعنی تخمینہ) کی توقع E اور اصل قیمت Y کے درمیان فرق کی وضاحت کرتا ہے۔ انحراف جتنا بڑا ہے ، اتنا ہی حقیقی اعداد و شمار سے دور ہے۔
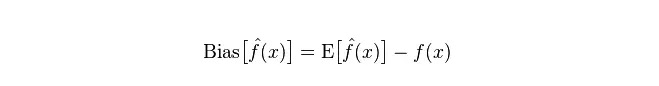
فاصلے: یہ وضاحت کرتا ہے کہ پی کی پیشن گوئی کی قیمت میں تبدیلی کی حد ، اور اس کی شدت ، پی کی پیشن گوئی کی قیمت کا فاصلہ ہے ، یعنی اس کی متوقع قیمت ای سے فاصلہ ہے۔ فاصلہ جتنا بڑا ہے ، اعداد و شمار کی تقسیم اتنی ہی بکھری ہوئی ہے۔
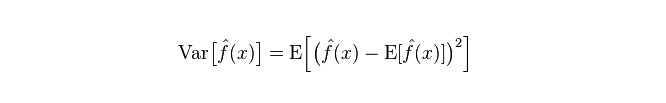
ماڈل کی حقیقی غلطی دونوں کا مجموعہ ہے، جیسا کہ ذیل میں دکھایا گیا ہے:
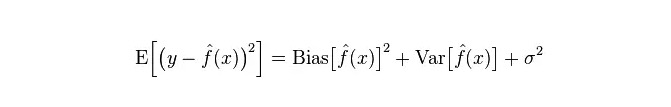
اگر یہ ایک چھوٹا تربیتی سیٹ ہے تو ، اعلی انحراف / کم انحراف کے درجہ بندی کرنے والے (مثال کے طور پر ، سادہ بیجسی این بی) کم انحراف / اعلی انحراف کے بڑے درجہ بندی کے مقابلے میں زیادہ فائدہ مند ہیں (مثال کے طور پر ، کے این این) ، کیونکہ مؤخر الذکر زیادہ فٹ ہوجاتا ہے۔
تاہم ، آپ کے ٹریننگ سیٹ میں اضافے کے ساتھ ، ماڈل اصل اعداد و شمار کی پیش گوئی کرنے کی صلاحیت میں بہتر ہوتا ہے ، اور اس میں کمی واقع ہوتی ہے۔ اس وقت کم انحراف / اعلی انحراف کے درجہ بندی کرنے والے آہستہ آہستہ اپنا فائدہ ظاہر کرتے ہیں (کیونکہ ان میں کم تدریجی غلطی ہوتی ہے) ، اس وقت اعلی انحراف کے درجہ بندی کرنے والے اس وقت درست ماڈل فراہم کرنے کے لئے ناکافی ہوجاتے ہیں۔
یقینا، آپ یہ بھی سوچ سکتے ہیں کہ یہ پیداواری ماڈل (NB) اور فیصلہ کن ماڈل (KNN) کے درمیان فرق ہے.
- ## اس کے علاوہ ، یہ بھی معلوم ہوتا ہے کہ بیزس کے بارے میں کیا کہا جاتا ہے کہ وہ ایک اعلی یا کم فاصلہ والا شخص ہے۔
اس کے بعد، مندرجہ ذیل بیانات ہیں:
سب سے پہلے ، فرض کریں کہ آپ کو تربیت اور ٹیسٹ سیٹ کا رشتہ معلوم ہے۔ آسان الفاظ میں ، ہم تربیت کے سیٹ پر ایک ماڈل سیکھنے جارہے ہیں ، اور پھر ٹیسٹ سیٹ حاصل کرنے کے لئے ، ٹیسٹ سیٹ کی غلطی کی شرح کے مطابق اثر انداز ہونا چاہئے۔
لیکن اکثر اوقات ہم صرف یہ فرض کر سکتے ہیں کہ ٹیسٹ سیٹ اور ٹریننگ سیٹ ایک ہی ڈیٹا ڈسٹری بیوشن کے مطابق ہیں، لیکن ہمیں اصل ٹیسٹ ڈیٹا نہیں ملتا۔ اس وقت صرف ٹریننگ کی غلطی کی شرح کو دیکھتے ہوئے ٹیسٹ کی غلطی کی شرح کی پیمائش کیسے کی جائے؟
چونکہ ٹریننگ کے نمونے بہت کم ہیں ((کم از کم کافی نہیں ہیں) ، لہذا ٹریننگ سیٹ کے ذریعہ حاصل کردہ ماڈل ہمیشہ حقیقی طور پر درست نہیں ہوتا ہے۔ ((اگر ٹریننگ سیٹ پر 100٪ درستگی بھی ہے تو ، اس کا مطلب یہ نہیں ہے کہ اس نے حقیقی اعداد و شمار کی تقسیم کو نقشہ کیا ہے ، یہ جاننا کہ حقیقی اعداد و شمار کی تقسیم کو نقشہ کرنا ہمارا مقصد ہے ، نہ کہ صرف ٹریننگ سیٹ کے محدود اعداد و شمار کے نقطہ کو نقشہ کرنا) ۔
اور ، عملی طور پر ، ٹریننگ کے نمونے میں اکثر شور کی غلطی بھی ہوتی ہے ، لہذا اگر ٹریننگ سیٹ پر کمال کے لئے بہت زیادہ کوشش کی جائے اور ایک بہت ہی پیچیدہ ماڈل استعمال کیا جائے تو ، اس سے ماڈل ٹریننگ سیٹ میں موجود غلطیوں کو حقیقی اعداد و شمار کی تقسیم کی خصوصیت کے طور پر لے جائے گا ، جس سے اعداد و شمار کی غلط تقسیم کا اندازہ لگایا جاسکتا ہے۔
اس طرح ، حقیقی ٹیسٹ سیٹ پر غلطی کا ایک دھندلا ہوا ہے (اس رجحان کو فٹنس کہا جاتا ہے) ۔ لیکن بہت آسان ماڈل بھی استعمال نہیں کیا جاسکتا ، ورنہ جب ڈیٹا کی تقسیم زیادہ پیچیدہ ہوتی ہے تو ، ماڈل اعداد و شمار کی تقسیم کو نقش کرنے کے لئے ناکافی ہوتا ہے (یہ ظاہر ہوتا ہے کہ یہاں تک کہ تربیتی سیٹ پر غلطی کی شرح بہت زیادہ ہے ، یہ رجحان فٹنس سے کم ہے) ۔
زیادہ فٹ ہونے کا مطلب یہ ہے کہ ماڈل حقیقی اعداد و شمار کی تقسیم سے زیادہ پیچیدہ ہے ، اور کم فٹ ہونے کا مطلب یہ ہے کہ ماڈل حقیقی اعداد و شمار کی تقسیم سے زیادہ آسان ہے۔
اعداد و شمار کے سیکھنے کے فریم ورک کے تحت ، جب ہم ماڈل کی پیچیدگی کا خاکہ پیش کرتے ہیں تو ، اس طرح کا نظریہ ہے کہ غلطی = تعصب + تغیر۔ یہاں غلطی کو شاید ماڈل کی پیش گوئی کی غلطی کی شرح کے طور پر سمجھا جاسکتا ہے ، جو دو حصوں پر مشتمل ہے ، ایک حصہ ماڈل کے بہت سادہ ہونے کی وجہ سے تخمینوں کی غلطیاں (تعصب) ، اور دوسرا حصہ ماڈل کے بہت پیچیدہ ہونے کی وجہ سے بڑے پیمانے پر تبدیلی کی جگہ اور غیر یقینی صورتحال (تفریق) ۔
لہذا ، اس طرح سادہ بیس کا تجزیہ کرنا آسان ہے۔ اس کا سادہ فرض ہے کہ اعداد و شمار کے مابین کوئی تعلق نہیں ہے ، ایک انتہائی آسان ماڈل ہے۔ لہذا ، اس طرح کے ایک سادہ ماڈل کے لئے ، زیادہ تر معاملات میں ، تعصب کا حصہ تغیر کے حصے سے بڑا ہوتا ہے ، یعنی اعلی انحراف اور کم فرق۔
عملی طور پر ، غلطی کو کم سے کم کرنے کے ل we ، ہمیں ماڈل کا انتخاب کرتے وقت تعصب اور تغیر کے تناسب کو متوازن کرنے کی ضرورت ہے ، یعنی اوور فٹنگ اور انڈر فٹنگ کو متوازن کرنا۔
مندرجہ ذیل گراف کے ذریعے اس بات کا اندازہ لگایا جا سکتا ہے کہ کسر اور فاریکس کے درمیان کیا تعلق ہے:
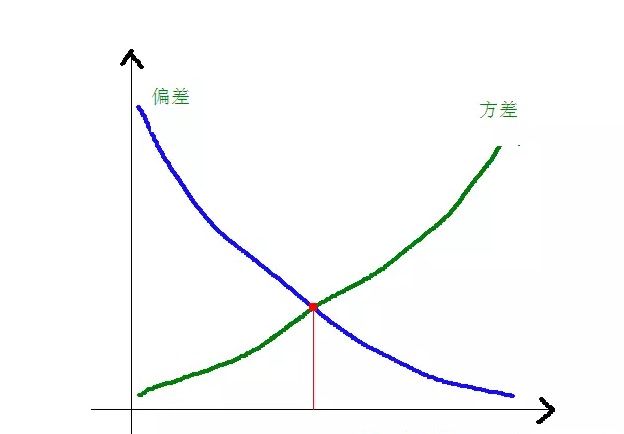
جب ماڈل کی پیچیدگی بڑھتی ہے، تو اس کی انحراف کم ہوتی ہے اور اس کی فاصلے میں اضافہ ہوتا ہے۔
-
عام الگورتھم کے فوائد اور نقصانات
- ### 1. نیکول بیٹس
سادہ Bayes پیداواری ماڈل (کے بارے میں پیداواری ماڈل اور تعیناتی ماڈل، بنیادی طور پر یہ ہے کہ آیا مشترکہ تقسیم کی ضرورت ہے) ، بہت آسان ہے، آپ کو صرف ایک بہت کچھ کیا ہے.
اگر مشروط آزادی کا مفروضہ دیا جائے (((ایک سخت تر شرط) ، تو سادہ بیس classifiers کی رفتار فیصلہ ماڈل سے زیادہ تیز ہوگی ، جیسے منطقی رجعت ، لہذا آپ کو صرف کم تربیتی اعداد و شمار کی ضرورت ہوگی۔ یہاں تک کہ اگر NB مشروط آزادی کا مفروضہ درست نہیں ہے ، تو NB classifiers عملی طور پر بہت اچھا کام کرتے ہیں۔
اس کی سب سے بڑی خرابی یہ ہے کہ یہ خصوصیات کے مابین باہمی تعامل کو نہیں سیکھ سکتا ہے۔ ایم آر ایم آر میں آر کے لئے ، خصوصیت کی ضرورت سے زیادہ ہے۔ ایک کلاسک مثال کے طور پر ، مثال کے طور پر ، اگرچہ آپ کو بریڈ پٹ اور ٹام کروز کی فلم پسند ہے ، لیکن یہ نہیں سیکھ سکتا ہے کہ آپ کو ان کی فلم پسند نہیں ہے۔
فوائد:
سادہ بییس ماڈل کلاسیکی ریاضیاتی نظریہ سے ماخوذ ہے ، جس کی ایک مضبوط ریاضیاتی بنیاد ہے ، اور اس کی درجہ بندی کی مستحکم کارکردگی ہے۔ چھوٹے پیمانے پر اعداد و شمار کے ساتھ اچھی کارکردگی کا مظاہرہ کرتا ہے، کثیر طبقاتی کاموں کو سنبھال سکتا ہے، اور اضافی تربیت کے لئے موزوں ہے؛ لاپتہ اعداد و شمار کے لئے زیادہ حساس نہیں ہے، اور الگورتھم نسبتا سادہ ہے، اکثر متن کی درجہ بندی کے لئے استعمال کیا جاتا ہے. نقصانات:
اس کا مطلب یہ ہے کہ آپ کو پہلے سے موجود امکانات کا حساب لگانے کی ضرورت ہے۔ درجہ بندی کے فیصلوں میں غلطی کی شرح؛ ان پٹ کے اعداد و شمار کے اظہار کی شکل پر حساس۔
- ### منطقی رجعت 2.
اس کے علاوہ، آپ کو آپ کی خصوصیت کے متعلقہ ہونے کے بارے میں فکر کرنے کی ضرورت نہیں ہے، جیسا کہ سادہ Bayes کی ہے.
فیصلہ درخت اور ایس وی ایم مشین کے مقابلے میں آپ کو ایک عمدہ احتمال کی تشریح بھی ملتی ہے ، اور آپ آسانی سے نئے اعداد و شمار کو ماڈل کو اپ ڈیٹ کرنے کے لئے استعمال کرسکتے ہیں (آن لائن گریڈینٹ نزول کا استعمال کرتے ہوئے) ۔
اگر آپ کو ایک امکانات کی ساخت کی ضرورت ہے (مثال کے طور پر، صرف درجہ بندی کی کمی کو ایڈجسٹ کرنے کے لئے، غیر یقینی صورتحال کی نشاندہی کرنے کے لئے، یا اعتماد کی حد حاصل کرنے کے لئے) ، یا آپ کو تیزی سے ماڈل میں زیادہ تر تربیتی اعداد و شمار کو ضم کرنا چاہتے ہیں، تو اس کا استعمال کریں.
سگمائڈ فنکشن:
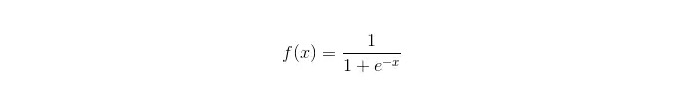
فوائد: سادہ اور وسیع پیمانے پر صنعتی مسائل پر لاگو؛ اس کے علاوہ ، یہ بھی کہا گیا ہے کہ یہ بہت کم کمپیوٹنگ ، تیز رفتار اور کم ذخیرہ کرنے والے وسائل کے ساتھ آتا ہے۔ آسان مشاہداتی نمونے کے امکانات کے اسکور؛ منطقی رجعت کے لئے ، کثیر کالمینیسی ایک مسئلہ نہیں ہے ، اور یہ L2 باقاعدگی کے ساتھ مل کر اس مسئلے کو حل کرسکتا ہے۔ نقصانات: جب خصوصیت کی جگہ بڑی ہے تو، منطقی رجعت کی کارکردگی اچھی نہیں ہے؛ فٹ ہونے کے لئے آسان، عام طور پر زیادہ درست نہیں بہت زیادہ خصوصیات یا متغیرات کو اچھی طرح سے سنبھالنے میں ناکامی؛ صرف دو درجہ بندی کے مسائل کو سنبھال سکتا ہے (اس بنیاد پر مشتق سافٹ میکس کثیر درجہ بندی کے لئے استعمال کیا جاسکتا ہے) ، اور اسے لکیری طور پر تقسیم کرنا ضروری ہے۔ غیر لکیری خصوصیات کے لئے، ایک تبدیلی کی ضرورت ہے؛
- ### 3. لکیری رجعت
لکیری رجعت رجعت کے لئے استعمال ہوتی ہے، جیسا کہ لاجسٹک رجعت درجہ بندی کے لئے استعمال نہیں ہوتی ہے۔ اس کا بنیادی خیال یہ ہے کہ کم سے کم بائنری ضرب کی شکل میں غلطی کے فنکشن کو گریڈینٹ ڈراپ ڈاؤن طریقہ کار کے ذریعہ بہتر بنایا جائے۔ اس کے علاوہ ، عام مساوات کے ذریعہ براہ راست پیرامیٹرز کے حل حاصل کیے جاسکتے ہیں ، جس کے نتیجے میں:
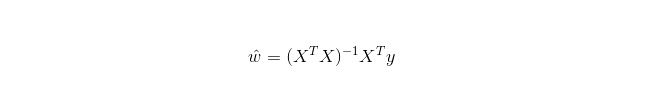
اور LWLR میں، پیرامیٹرز کے لئے حساب کا اظہار ہے:
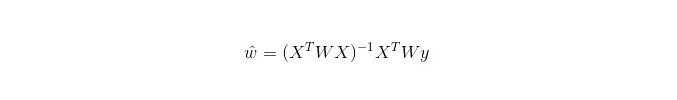
اس سے یہ ظاہر ہوتا ہے کہ ایل ڈبلیو ایل آر ایل آر سے مختلف ہے ، ایل ڈبلیو ایل آر ایک غیر پیرامیٹرڈ ماڈل ہے ، کیونکہ ہر بار جب رجعت کا حساب کتاب کیا جاتا ہے تو کم از کم ایک بار ٹریننگ کے نمونے پر جانا پڑتا ہے۔
فوائد: آسانی سے قابل عمل، آسان حساب؛
نقصانات: غیر لکیری اعداد و شمار کو فٹ نہیں کیا جا سکتا.
- ### 4. قریبی پڑوسی الگورتھم KNN
KNN یعنی قریبی ہمسایہ الگورتھم، جس کا بنیادی عمل یہ ہے:
تربیت کے نمونے اور ٹیسٹ کے نمونے میں ہر نمونے کے نقطہ کی فاصلے کا حساب لگائیں (عام فاصلے کی پیمائش یوروپی فاصلے ، مارسٹری فاصلے وغیرہ کے ساتھ) ۔
تمام فاصلے کی اقدار کو ترتیب دیں؛
پہلے سے منتخب کردہ k کم سے کم فاصلے کے نمونے؛
اس کے بعد ، اس کے بعد ، اس کے بعد ، اس کے بعد ، اس کے بعد ، اس کے بعد ، اس کے بعد ، اس کے بعد۔
ایک بہترین K ویلیو کا انتخاب کیسے کیا جاتا ہے، اس کا انحصار اعداد و شمار پر ہے۔ عام طور پر، درجہ بندی کے وقت ایک بڑی K ویلیو شور کے اثرات کو کم کرتی ہے۔ لیکن زمرے کے درمیان حدود کو دھندلا کر دیتی ہے۔
ایک بہتر K ویلیو مختلف الیکشن ٹیکنالوجیز کے ذریعہ حاصل کی جاسکتی ہے ، مثال کے طور پر ، کراس کی توثیق۔ اس کے علاوہ ، شور اور غیر متعلقہ خصوصیت والے ویکٹر کی موجودگی K قریبی پڑوسی الگورتھم کی درستگی کو کم کرتی ہے۔
قریبی پڑوسی الگورتھم کے مضبوط مستقل نتائج ہیں۔ اعداد و شمار کے لامحدود ہونے کے ساتھ ، الگورتھم کی غلطی کی ضمانت نہیں ہوتی ہے جو Bayesian الگورتھم کی غلطی کی دوگنا سے زیادہ ہے۔ کچھ اچھی K اقدار کے ل K قریبی پڑوسی کی غلطی کی ضمانت نہیں ہوتی ہے جو Bayesian نظریاتی غلطی سے زیادہ نہیں ہوتی ہے۔
KNN الگورتھم کی خصوصیات
نظریاتی پختگی، سادہ خیالات، جو درجہ بندی یا رجعت کے لئے استعمال کیا جا سکتا ہے؛ غیر لکیری درجہ بندی کے لئے استعمال کیا جا سکتا ہے؛ ٹریننگ وقت کی پیچیدگی O ((n) ہے؛ اعداد و شمار کے بارے میں کوئی مفروضہ نہیں ہے ، یہ انتہائی درست ہے اور آؤٹ لیئر کے بارے میں حساس نہیں ہے۔ کمی
بہت زیادہ حساب کتاب؛ نمونے کی عدم توازن (یعنی کچھ زمروں میں نمونے کی تعداد بہت زیادہ ہے جبکہ دوسرے نمونے کی تعداد بہت کم ہے) ؛ اس کے علاوہ، یہ بہت زیادہ میموری کی ضرورت ہوتی ہے.
- ### فیصلہ درخت
وضاحت کرنے میں آسان۔ یہ خصوصیات کے مابین باہمی تعامل کو بغیر کسی دباؤ کے اور غیر پیرامیٹرڈ کے ساتھ سنبھال سکتا ہے ، لہذا آپ کو اس بارے میں فکر کرنے کی ضرورت نہیں ہے کہ آیا غیر معمولی اقدار یا اعداد و شمار لکیری طور پر الگ ہوسکتے ہیں (مثال کے طور پر ، فیصلہ کرنے والا درخت آسانی سے اس معاملے کو سنبھال سکتا ہے کہ زمرہ A کسی خاص خصوصیت کی طول و عرض x کے آخر میں ، زمرہ B وسط میں ، اور پھر زمرہ A خصوصیت کی طول و عرض x کے سامنے کے اختتام پر) ۔
اس میں ایک خرابی یہ بھی ہے کہ یہ آن لائن سیکھنے کی حمایت نہیں کرتا ہے، لہذا جب نئے نمونے آتے ہیں تو فیصلہ کرنے والے درخت کو مکمل طور پر دوبارہ تعمیر کرنا پڑتا ہے.
ایک اور خرابی یہ ہے کہ یہ آسانی سے زیادہ فٹ بیٹھتا ہے ، لیکن یہ انضمام کے طریقوں کا ایک نقطہ ہے جیسے بے ترتیب جنگل آر ایف ((یا درخت کو فروغ دینے والا درخت)) ۔
اس کے علاوہ ، رینڈم جنگل اکثر درجہ بندی کے مسائل میں فاتح ہوتا ہے (عام طور پر سپورٹ ویکٹر مشینوں کے مقابلے میں تھوڑا سا بہتر) ، یہ تربیت دینے میں تیز اور قابل تدوین ہے ، اور آپ کو سپورٹ ویکٹر مشینوں کی طرح بہت سارے پیرامیٹرز کو ایڈجسٹ کرنے کی فکر کرنے کی ضرورت نہیں ہے ، لہذا یہ پہلے بھی مقبول رہا ہے۔
فیصلہ کے درخت میں ایک اہم بات یہ ہے کہ ایک خاصیت کو شاخوں کے لئے منتخب کیا جائے۔ لہذا ، معلوماتی اضافے کے حساب کتاب کے فارمولے پر دھیان دیں اور اس کی گہرائی میں سمجھیں۔
انفارمیشن باکس کا حساب کتاب مندرجہ ذیل ہے:
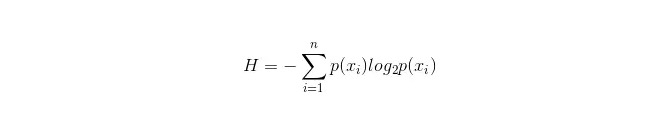
اس میں n نمائندگی کرتا ہے کہ n درجہ بندی کی اقسام ہیں ((مثال کے طور پر فرض کریں کہ یہ 2 قسم کے سوالات ہیں ، تو پھر n = 2) ۔ مجموعی نمونے میں ان 2 قسم کے نمونے کے ظاہر ہونے کے امکانات p1 اور p2 کو الگ الگ شمار کریں ، تاکہ غیر منتخب کردہ صفات کی شاخ سے پہلے کی معلومات کا حساب لگایا جاسکے۔
اب ایک خاصیت xxi منتخب کی جائے جو شاخوں کے لئے استعمال کی جائے۔ اس وقت شاخوں کا قاعدہ یہ ہے: اگر x = vxi = v ہے تو ، نمونہ کو درخت کی ایک شاخ میں تقسیم کریں۔ اگر یہ مساوی نہیں ہے تو ، دوسری شاخ میں جائیں۔
واضح طور پر ، شاخوں میں نمونے میں 2 زمرے شامل ہونے کا امکان ہے ، بالترتیب ان دو شاخوں کے H1 اور H2 کو حساب لگائیں ، اور اس وقت معلومات میں اضافے کے لئے H1 = p1 H1 + p2 H2 ، اس وقت معلومات میں اضافے کے لئے ΔH = H - H2 کا حساب لگائیں۔ معلومات میں اضافے کے اصول پر عمل کرتے ہوئے ، تمام خصوصیات کو ایک ساتھ ٹیسٹ کریں ، اور اس بار شاخوں کی خصوصیت کے طور پر سب سے زیادہ اضافے والی خصوصیت کو منتخب کریں۔
فیصلے کے درختوں کے فوائد
اس کے علاوہ ، یہ بھی کہا گیا ہے کہ یہ ایک بہت ہی آسان اور قابل فہم طریقہ ہے۔ نمونے کے ساتھ نمٹنے کے لئے زیادہ مناسب ہے جس میں خصوصیات کی کمی ہے؛ غیر متعلقہ خصوصیت کو سنبھالنے کی صلاحیت؛ ایک نسبتا مختصر وقت میں بڑے اعداد و شمار کے ذرائع کے لئے قابل عمل اور مؤثر نتائج پیدا کرنے کے قابل ہونا. کمی
اوور فٹ ہونے کا خطرہ (بے ترتیب جنگلات میں اوور فٹ ہونے میں نمایاں کمی واقع ہوسکتی ہے) اعداد و شمار کے درمیان تعلق کو نظر انداز کرنا؛ ان اعداد و شمار کے لئے جو مختلف زمروں کے نمونے کی تعداد میں متضاد ہیں ، فیصلہ کن درختوں میں ، معلومات میں اضافے کے نتائج ان لوگوں کی طرف راغب ہوتے ہیں جن کی خصوصیات میں زیادہ تعداد ہوتی ہے ((جب تک کہ معلومات میں اضافے کا استعمال کیا جاتا ہے ، اس کا نقصان ہوتا ہے ، جیسے آر ایف)) ۔
- ### 5.1 Adaboosting
اڈابوسٹ ایک اضافے کا ماڈل ہے ، جس میں ہر ماڈل پچھلے ماڈل کی غلطی کی شرح پر مبنی ہوتا ہے ، غلطی والے نمونے پر زیادہ توجہ دیتے ہیں ، اور صحیح درجہ بندی والے نمونے پر کم توجہ دیتے ہیں ، اور بار بار تکرار کے بعد ، ایک نسبتا better بہتر ماڈل حاصل کیا جاسکتا ہے۔ یہ ایک عام فروغ دینے والا الگورتھم ہے۔ ذیل میں اس کے فوائد اور نقصانات کا خلاصہ کیا گیا ہے۔
فائدہ
adaboost ایک اعلی صحت سے متعلق درجہ بندی والا ہے۔ مختلف طریقوں سے ذیلی درجہ بندی کی تعمیر کی جا سکتی ہے، Adaboost الگورتھم فریم ورک فراہم کرتا ہے. جب سادہ درجہ بندی کا استعمال کیا جاتا ہے تو ، حساب کتاب کے نتائج قابل فہم ہوتے ہیں ، اور کمزور درجہ بندی کی تعمیر انتہائی آسان ہوتی ہے۔ آسان، کوئی خصوصیت فلٹرنگ نہیں اوور فٹنگ کا خطرہ۔ بے ترتیب جنگل اور GBDT جیسے مجموعی الگورتھم کے بارے میں ، اس مضمون کو دیکھیں: مشین لرننگ - مجموعی الگورتھم کا خلاصہ
نقصانات: آؤٹ لیئر حساسیت
- ### 6. SVM حمایت ویکٹر مشین
اعلی درستگی ، اوور فٹ ہونے سے بچنے کے لئے ایک عمدہ نظریاتی گارنٹی فراہم کرتی ہے ، اور یہاں تک کہ اگر اعداد و شمار اصل خصوصیت کی جگہ میں لکیری طور پر ناقابل تقسیم ہوں ، تو یہ ایک مناسب بنیادی فنکشن دیئے جانے پر اچھی طرح سے کام کرسکتا ہے۔
متحرک اور انتہائی اعلی درجے کی ٹیکسٹ درجہ بندی کے مسائل میں خاص طور پر مقبول ہے۔ افسوس کی بات ہے کہ یہ میموری کی کھپت ہے ، اس کی تشریح کرنا مشکل ہے ، اور اس کے ساتھ ساتھ چلنے اور اس کی مثال دینا بھی کچھ پریشان کن ہے ، اور بے ترتیب جنگل ان خرابیوں سے بچنے کے لئے کافی عملی ہے۔
فائدہ اس کے علاوہ، اس کے علاوہ، اس کے علاوہ، اس کے علاوہ، اس کے علاوہ. غیر لکیری خصوصیت کے تعامل کو سمجھنے کی صلاحیت؛ اس کے علاوہ ، یہ بھی کہا گیا ہے کہ: اس کے علاوہ ، یہ بھی کہا گیا ہے کہ:
کمی اس کے علاوہ ، یہ بھی معلوم ہوتا ہے کہ جب بہت سارے نمونے دیکھے جاتے ہیں تو بہت زیادہ کارکردگی نہیں ہوتی ہے۔ غیر لکیری مسائل کے لئے کوئی عام حل نہیں ہے، اور بعض اوقات ایک مناسب بنیادی فنکشن تلاش کرنا مشکل ہے؛ ڈیٹا کے فقدان کے بارے میں حساس؛ کور کے انتخاب کے لئے بھی ہنر مند ہے (libsvm میں چار قسم کے کور فنکشن ہیں: لکیری کور ، کثیر جہتی کور ، RBF ، اور سگمائڈ کور):
سب سے پہلے ، اگر نمونے کی تعداد خصوصیت کی تعداد سے کم ہے تو ، غیر لکیری کور کا انتخاب کرنے کی ضرورت نہیں ہے ، صرف لکیری کور کا استعمال کیا جاسکتا ہے۔
دوسرا ، اگر نمونے کی تعداد خصوصیت کی تعداد سے زیادہ ہے تو ، غیر لکیری کور استعمال کیا جاسکتا ہے ، جس سے نمونے کو اعلی جہت میں نقشہ بنایا جاسکتا ہے ، جس سے عام طور پر بہتر نتائج برآمد ہوتے ہیں۔
تیسرا ، اگر نمونے کی تعداد اور خصوصیات کی تعداد برابر ہے تو ، اس صورت میں غیر لکیری کور استعمال کیا جاسکتا ہے ، اسی اصول کے ساتھ جیسے دوسرا۔
پہلی صورت کے لئے، آپ کو پہلے اعداد و شمار کو کم کرنے اور پھر غیر لکیری کور کا استعمال کر سکتے ہیں، جو بھی ایک طریقہ ہے.
- ### 7. مصنوعی اعصابی نیٹ ورک کے فوائد اور نقصانات
مصنوعی اعصابی نیٹ ورک کے فوائد: درجہ بندی کی اعلی درستگی؛ ہم آہنگی میں تقسیم شدہ پروسیسنگ، تقسیم شدہ اسٹوریج اور سیکھنے کی صلاحیتیں مضبوط ہیں. شور کی اعصاب کے لئے مضبوط روبوبلٹی اور غلطی برداشت کرنے کی صلاحیت ، جو پیچیدہ غیر لکیری تعلقات کے لئے کافی قریب ہے؛ اس کے علاوہ، اس کے علاوہ، اس کے علاوہ، اس کے علاوہ، اس کے علاوہ.
مصنوعی اعصابی نیٹ ورکس کے نقصانات: نیورل نیٹ ورکس کو بہت سارے پیرامیٹرز کی ضرورت ہوتی ہے ، جیسے نیٹ ورک ٹوپولوجیکل ڈھانچہ ، ابتدائی اقدار اور ابتدائی اقدار۔ اس کے نتیجے میں ، یہ سیکھنے کے عمل کو دیکھنے کے قابل نہیں ہے ، اور نتائج کی تشریح کرنا مشکل ہے ، جو نتائج کی وشوسنییتا اور قبولیت کو متاثر کرتا ہے۔ آپ کے لیے یہ بہت لمبا ہے اور شاید آپ اپنے مقصد تک نہیں پہنچ پائیں گے۔
- ### 8، K-Means گروپ بندی
K-Means clusters کے بارے میں پہلے بھی ایک مضمون لکھا گیا ہے، اس میں بہت مضبوط EM خیالات ہیں۔
فائدہ یہ الگورتھم سادہ اور لاگو کرنے میں آسان ہے۔ بڑے اعداد و شمار کے سیٹ کے ساتھ کام کرنے کے لئے ، یہ الگورتھم نسبتا scalable اور موثر ہے ، کیونکہ اس کی پیچیدگی تقریبا O ((nkt) ہے ، جہاں n تمام اشیاء کی تعداد ہے ، k جھرنوں کی تعداد ہے ، اور t تکرار کی تعداد ہے۔ عام طور پر k < < n ہے۔ یہ الگورتھم عام طور پر مقامی طور پر متفق ہوتا ہے۔ < p=“”> الگورتھم کوشش کرتا ہے کہ اس کے لئے کم سے کم k تقسیم تلاش کریں تاکہ اس کی مربع غلطی کی تقریب کی قدر کم سے کم ہو۔ جب فوم گھنے ، گول یا گھنے ہوتے ہیں ، اور فوم اور فوم کے درمیان واضح فرق ہوتا ہے تو ، کلسٹرنگ بہتر ہوتا ہے۔
کمی اعداد و شمار کی قسم کے لئے اعلی ضروریات، عددی اعداد و شمار کے لئے موزوں؛ ممکنہ طور پر مقامی کم سے کم اور بڑے پیمانے پر اعداد و شمار پر آہستہ آہستہ K قدر کو منتخب کرنا مشکل ہے؛ ابتدائی قیمتوں کے لئے توجہ مرکوز کی قیمت حساس، مختلف ابتدائی اقدار کے لئے، مختلف clustering کے نتائج کا سبب بن سکتا ہے؛ غیر موڑنے والی شکلیں یا بڑے پیمانے پر مختلف سائز کے جھاڑیوں کو تلاش کرنے کے لئے موزوں نہیں ہے۔ اس طرح کے اعداد و شمار کی ایک چھوٹی سی مقدار اوسط پر بہت زیادہ اثر ڈال سکتی ہے۔
الگورتھم منتخب حوالہ
اس سے پہلے، میں نے بیرون ملک مقالے کا ترجمہ کیا تھا، اور ایک مضمون میں ایک آسان الگورتھم منتخب کرنے کا مشورہ دیا گیا تھا:
سب سے پہلے اس کا انتخاب کرنا چاہئے منطقی رجعت ہے ، اگر اس کا اثر اتنا اچھا نہیں ہے تو ، اس کے نتائج کو ایک معیار کے طور پر حوالہ دیا جاسکتا ہے ، جس کی بنیاد پر دوسرے الگورتھم کے ساتھ موازنہ کیا جاسکتا ہے۔
اس کے بعد فیصلہ کے درختوں (بے ترتیب جنگل) کو آزمائیں اور دیکھیں کہ کیا آپ اپنے ماڈل کی کارکردگی کو نمایاں طور پر بڑھا سکتے ہیں۔ یہاں تک کہ اگر آپ اسے حتمی ماڈل کے طور پر نہیں لیتے ہیں تو ، آپ کو خاصیت کے انتخاب کے لئے شور متغیرات کو ہٹانے کے لئے بے ترتیب جنگل کا استعمال کرنا چاہئے۔
اگر خصوصیات کی تعداد اور مشاہدے کے نمونے خاص طور پر زیادہ ہیں، تو جب وسائل اور وقت کافی ہے (یہ شرط اہم ہے) ، ایس وی ایم کا استعمال ایک اختیار ہے.
عام طور پر: GBDT> = SVM> = RF> = Adaboost> = Other… ، اب گہرائی سے سیکھنا بہت مقبول ہے، بہت سے شعبوں میں استعمال کیا جاتا ہے، یہ نیورل نیٹ ورک پر مبنی ہے، میں خود بھی سیکھ رہا ہوں، صرف نظریاتی علم بہت گہرا نہیں ہے، سمجھنے کے لئے کافی گہرائی نہیں ہے، یہاں تعارف نہیں کیا جائے گا۔
الگورتھم ضروری ہے، لیکن اچھے اعداد و شمار اچھے الگورتھم سے بہتر ہیں، اور اچھی طرح سے ڈیزائن کردہ خصوصیات بہت فائدہ مند ہیں. اگر آپ کے پاس ایک بہت بڑا ڈیٹا سیٹ ہے، تو آپ جو بھی الگورتھم استعمال کرتے ہیں وہ درجہ بندی کی کارکردگی پر بہت زیادہ اثر انداز نہیں ہوسکتے ہیں (اس وقت آپ کی رفتار اور استعمال میں آسانی کی بنیاد پر انتخاب کیا جا سکتا ہے).
-
حوالہ جات