ایل ایس ٹی ایم فریم ورک کا استعمال کرتے ہوئے حقیقی وقت میں بٹ کوائن کی قیمت کی پیشن گوئی کریں

ٹپ: یہ کیس صرف مطالعہ اور تحقیق کے مقاصد کے لئے ہے اور یہ سرمایہ کاری کی تجویز نہیں ہے۔

بٹ کوائن کی قیمت کے اعداد و شمار وقت کی ترتیب پر مبنی ہیں ، لہذا بٹ کوائن کی قیمت کی پیش گوئی زیادہ تر LSTM ماڈل کے ذریعہ کی جاتی ہے۔

طویل مدتی مختصر میموری (LSTM) ایک گہری سیکھنے کا ماڈل ہے جو خاص طور پر وقت کے سلسلے کے اعداد و شمار (یا وقت / خلائی / ساختہ ترتیب والے اعداد و شمار ، جیسے فلمیں ، جملے ، وغیرہ) کے لئے موزوں ہے ، جو ایک کریپٹوکرنسی کی قیمت کی سمت کی پیش گوئی کرنے کا ایک مثالی ماڈل ہے۔

یہ مضمون بنیادی طور پر ایل ایس ٹی ایم کے ذریعہ اعداد و شمار کو جوڑنے کے بارے میں لکھا گیا ہے تاکہ بٹ کوائن کی مستقبل کی قیمت کی پیش گوئی کی جاسکے۔

درآمد کرنے کے لئے استعمال شدہ لائبریری

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

ڈیٹا تجزیہ

ڈیٹا لوڈ

بی ٹی سی کے روزانہ ٹریڈنگ کے اعداد و شمار کو پڑھیں

data = pd.read_csv(filepath_or_buffer="btc_data_day")

اعداد و شمار کو دیکھنے کے لئے دستیاب ہے، اس وقت اعداد و شمار کی کل تعداد 1380 ہے۔ اعداد و شمار کی کالمیں Date، Open، High، Low، Close، Volume ((BTC) ، Volume ((Currency) ، Weighted Price پر مشتمل ہیں۔ ان میں سے Date کالم کو چھوڑ کر باقی کالم float64 ڈیٹا ٹائپ کے ہیں۔

data.info()

مندرجہ ذیل 10 صفوں میں اعداد و شمار دیکھیں

data.head(10)

اعداد و شمار کی نمائش

ہم نے اعداد و شمار کی تقسیم اور رجحانات کو دیکھنے کے لئے وزن شدہ قیمتوں کا استعمال کرتے ہوئے استعمال کیا ہے۔ اس گراف میں ہم نے اعداد و شمار کے ایک حصے کو دیکھا ہے جہاں 0 ہے اور ہمیں اس بات کی تصدیق کرنے کی ضرورت ہے کہ آیا اعداد و شمار میں کوئی خرابی ہے یا نہیں۔

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

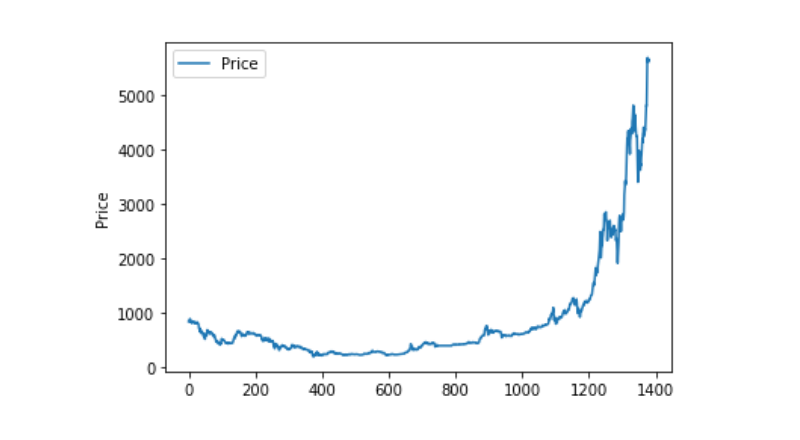
غیر معمولی ڈیٹا پروسیسنگ

ہم نے پہلے یہ دیکھا کہ کیا ہمارے ڈیٹا میں نانی اعداد و شمار موجود ہیں، اور ہم نے دیکھا کہ ہمارے ڈیٹا میں نانی اعداد و شمار موجود نہیں ہیں۔

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

اگر آپ 0 اعداد و شمار کو دوبارہ دیکھیں تو آپ دیکھیں گے کہ ہمارے اعداد و شمار میں 0 کی قدر موجود ہے اور ہمیں اس پر عمل کرنا ہوگا۔

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

اور پھر اعداد و شمار کی تقسیم اور رفتار کو دیکھیں، اور اس وقت، یہ منحنی خطوط بہت مسلسل ہیں.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

ٹریننگ ڈیٹا سیٹ اور ٹیسٹ ڈیٹا سیٹ کی تقسیم

اعداد و شمار کو 0 سے 1 تک اکٹھا کریں

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

ٹیسٹ ڈیٹا سیٹ اور ٹریننگ ڈیٹا سیٹ کو 2:8 میں تقسیم کریں۔

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

ٹریننگ ڈیٹا سیٹ اور ٹیسٹ ڈیٹا سیٹ بنائیں۔ ایک دن کے طور پر ونڈو کے طور پر ہمارے ٹریننگ ڈیٹا سیٹ اور ٹیسٹ ڈیٹا سیٹ کو تخلیق کریں۔

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

ماڈل کی وضاحت اور تربیت

اس بار ہم نے ایک سادہ ماڈل استعمال کیا ہے جس کی ساخت مندرجہ ذیل ہے۔ 1. LSTM2. Dense.

یہاں آپ کو ایل ایس ٹی ایم کے ان پٹ شکل کے بارے میں وضاحت کرنے کی ضرورت ہے۔ ان پٹ شکل کے ان پٹ طول و عرض batch_size, time steps, features ہیں۔ یہاں، time steps کی قدر ڈیٹا ان پٹ کے وقت کے وقت ونڈو وقفہ ہے، یہاں ہم 1 دن کو وقت ونڈو کے طور پر استعمال کرتے ہیں، اور ہمارے اعداد و شمار دن کے اعداد و شمار ہیں، لہذا یہاں ہمارے وقت کے اقدامات 1 ہیں۔

لمبی مختصر مدت کی یادداشت (LSTM) ایک خاص RNN ہے جو بنیادی طور پر لمبی سیریز کی تربیت کے دوران گرڈینٹ کی گمشدگی اور گرڈینٹ کے دھماکے کے مسائل کو حل کرنے کے لئے استعمال ہوتی ہے۔

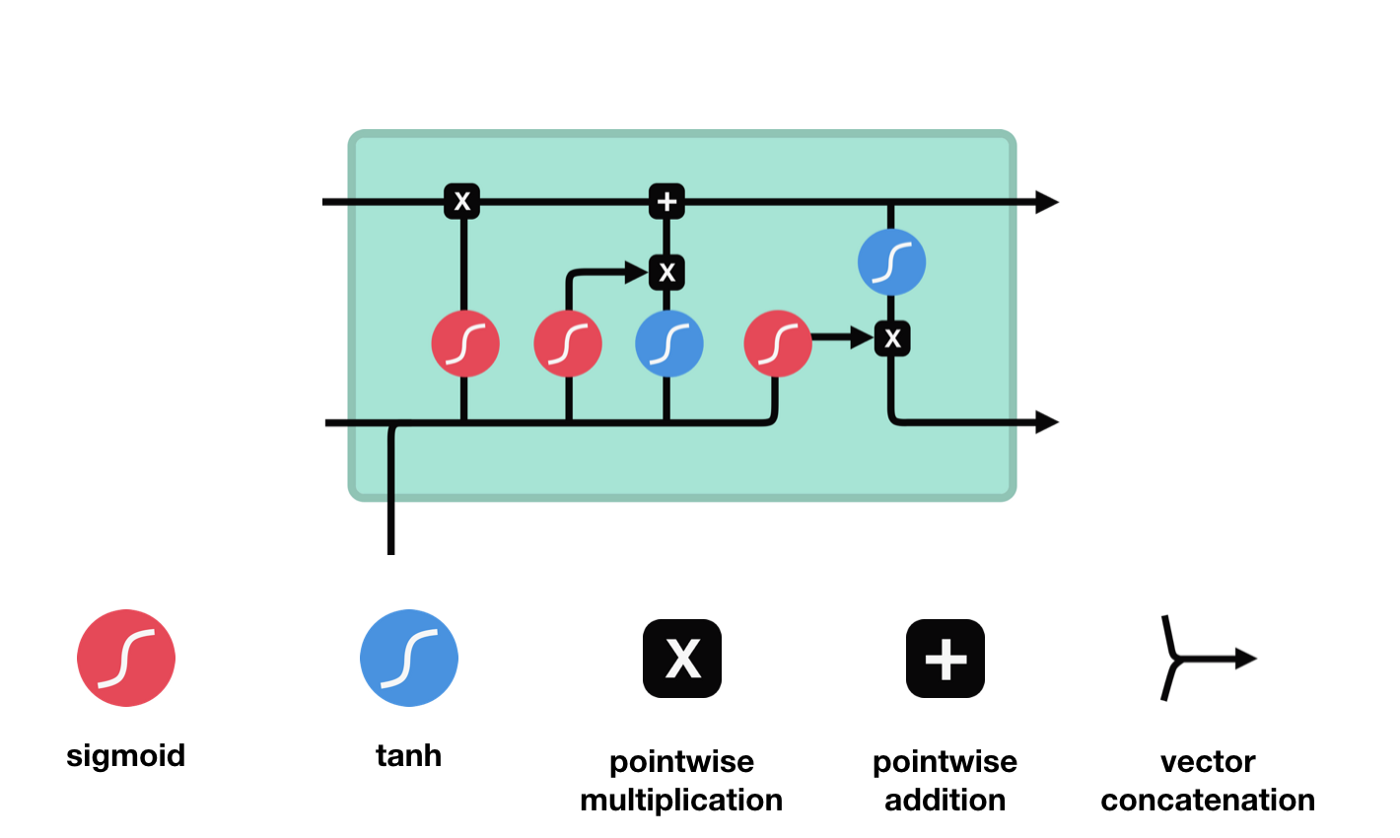
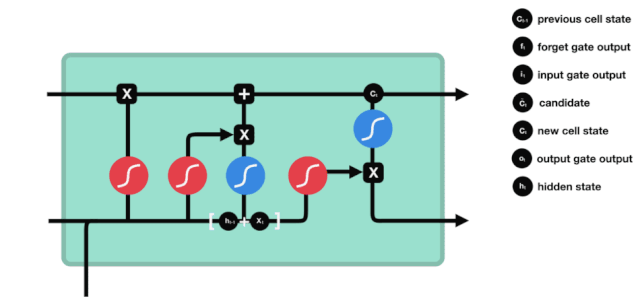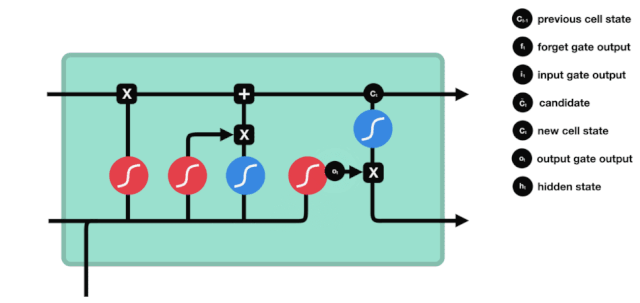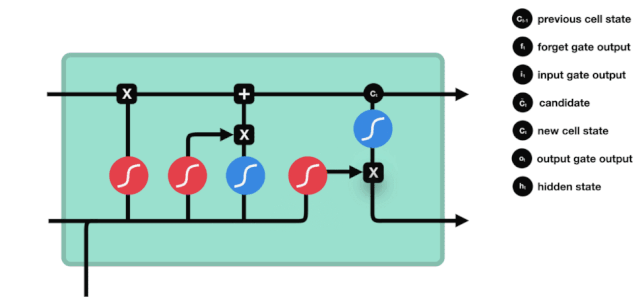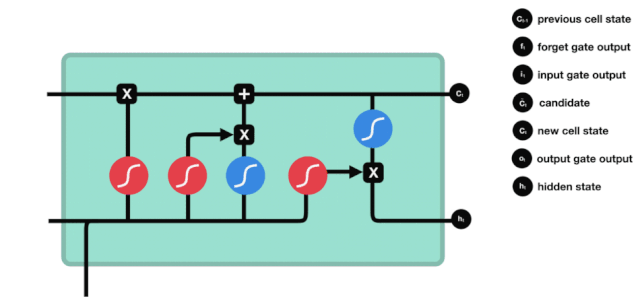
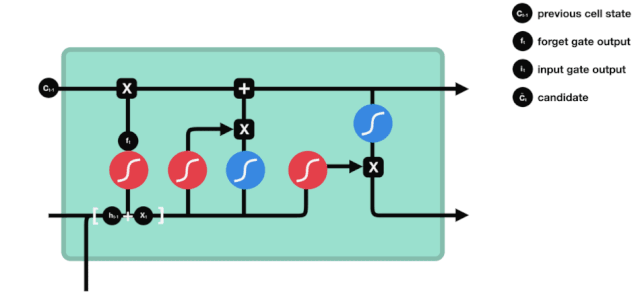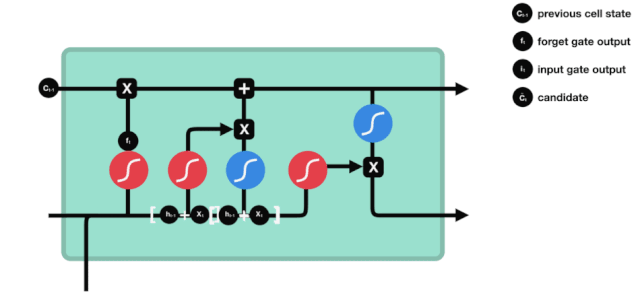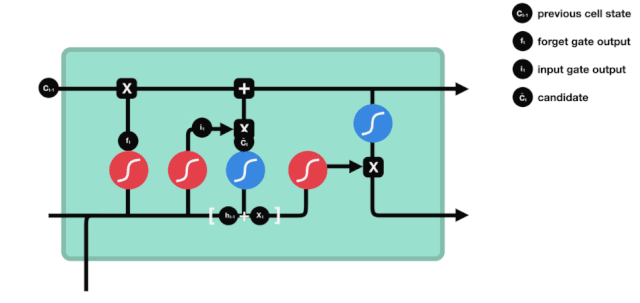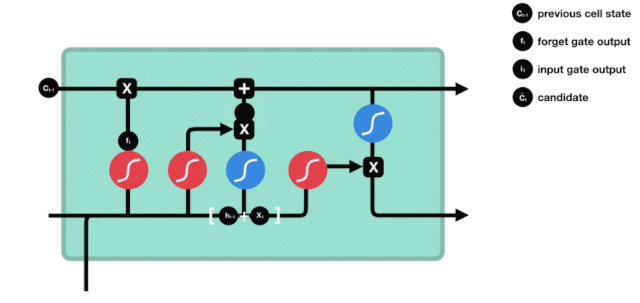
ایل ایس ٹی ایم کے نیٹ ورک کے ڈھانچے کے نقشے سے یہ دیکھا جاسکتا ہے کہ ایل ایس ٹی ایم دراصل ایک چھوٹا سا ماڈل ہے ، جس میں 3 سگموڈ چالو کرنے والے افعال ، 2 ٹینہ چالو کرنے والے افعال ، 3 ضرب اور ایک اضافہ شامل ہیں۔

خلیات کی حالت

سیل کی حالت LSTM کے مرکز میں ہے، وہ اوپر دی گئی تصویر میں سب سے اوپر کی سیاہ لائن ہے، اس کے نیچے کچھ دروازے ہیں، جن کا ہم بعد میں ذکر کریں گے۔ سیل کی حالت ہر دروازے کے نتائج کے مطابق اپ ڈیٹ ہوتی ہے۔ ذیل میں ہم ان دروازوں کا ذکر کرتے ہیں، آپ کو سیل کی حالت کے عمل کو سمجھنے میں مدد ملتی ہے۔

ایل ایس ٹی ایم نیٹ ورک خلیات کی حالت کے بارے میں معلومات کو حذف یا شامل کرتا ہے۔ دروازے کو یہ فیصلہ کرنے کی صلاحیت ہوتی ہے کہ کون سی معلومات گزرتی ہیں۔ دروازے کا ڈھانچہ سیگموڈ لیئر اور ایک نقطہ ضرب آپریشن کا ایک مجموعہ ہے۔ کیونکہ سیگموڈ لیئر کی پیداوار 0 سے 1 ہے ، 0 کا مطلب ہے کہ کوئی بھی گزر نہیں سکتا ہے ، اور 1 کا مطلب ہے کہ یہ گزر سکتا ہے۔ ایک ایل ایس ٹی ایم میں تین دروازے ہیں جو خلیات کی حالت کو کنٹرول کرتے ہیں۔ ذیل میں ہم ان دروازوں کو ایک ایک کرکے متعارف کراتے ہیں۔

بھولے دروازے

LSTM کا پہلا مرحلہ یہ طے کرنا ہے کہ سیل کی حالت کو کس معلومات کو ضائع کرنے کی ضرورت ہے۔ یہ حصہ ایک سیگمائڈ یونٹ کے ذریعہ عملدرآمد کیا جاتا ہے جسے بھولنے کا دروازہ کہا جاتا ہے۔ آئیے متحرک ڈرائنگ کو دیکھیں ، جس میں یہ ظاہر ہوتا ہے کہ سیلز کی حالت کو ضائع کرنے کی ضرورت ہے۔

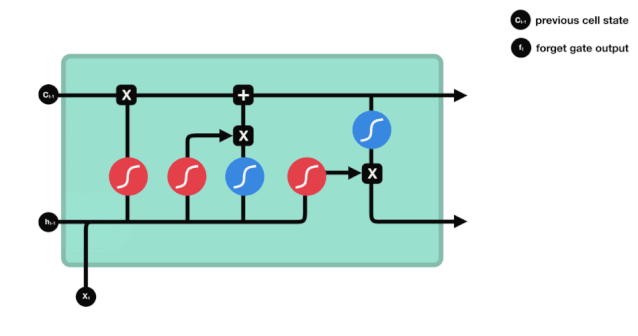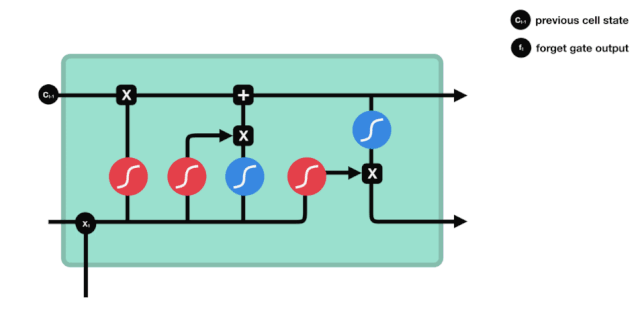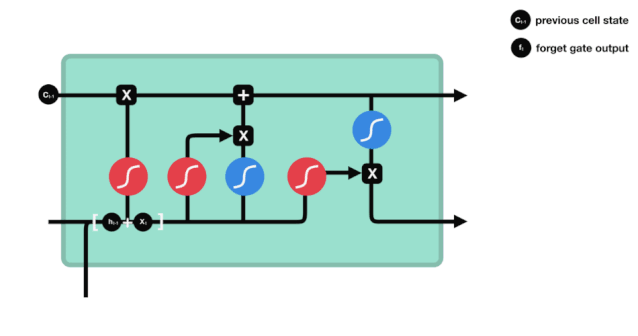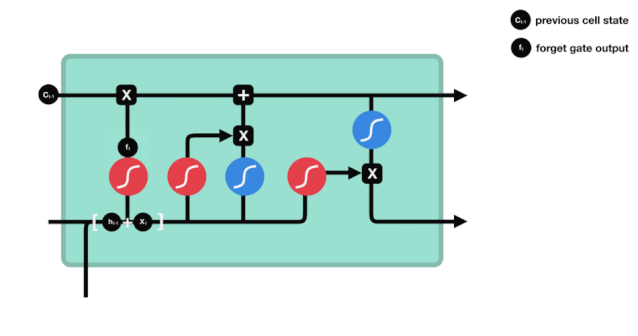
ہم دیکھ سکتے ہیں کہ بھولنے کا دروازہ $h_{l-1}$ اور $x_{t}$ پیغامات کو دیکھ کر 0 سے 1 کے درمیان ایک ویکٹر نکالتا ہے۔ اس ویکٹر میں 0 سے 1 کی قدر یہ بتاتی ہے کہ خلیے کی حالت $C_{t-1}$ میں کتنی معلومات کو برقرار رکھا یا ضائع کیا گیا۔ 0 کا مطلب ہے کہ برقرار نہیں رکھا گیا ہے۔ 1 کا مطلب ہے کہ یہ برقرار رکھا گیا ہے۔

ریاضیاتی اظہار: $f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}، x_{t}\right]+b_{f}\right) $

ان پٹ

اگلا مرحلہ یہ فیصلہ کرنا ہے کہ سیل کی حالت میں کون سی نئی معلومات شامل کی جائیں۔ یہ مرحلہ ان پٹ کے ذریعے کیا جاتا ہے۔

ہم دیکھتے ہیں کہ $h_{l-1}$ اور $x_{t}$ کی معلومات کو ایک بار پھر ایک بھول دروازے (sigmoid) اور ان پٹ دروازے (tanh) میں ڈال دیا جاتا ہے۔ کیونکہ بھول دروازے کا آؤٹ پٹ 0 کی قدر ہے، لہذا اگر بھول دروازے کا آؤٹ پٹ 0 ہے، تو ان پٹ کے بعد کا نتیجہ $C_{i}$ موجودہ سیل ریاست میں شامل نہیں کیا جائے گا، اگر 1 ہے، تو یہ سب سیل ریاست میں شامل کیا جائے گا، لہذا یہاں بھول دروازے کا کام ان پٹ دروازے کے نتائج کو سیل ریاست میں انتخابی طور پر شامل کرنا ہے۔

ریاضی کا فارمولا ہے: $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t} $

آؤٹ پٹ

خلیات کی حالت کو اپ ڈیٹ کرنے کے بعد ان پٹ $h_{l-1}$ اور $x_{t}$ کے مطابق کون سی حالت کی خصوصیات کا فیصلہ کرنے کی ضرورت ہوتی ہے ، یہاں ان پٹ کو ایک sigmoid پرت کے ذریعے جانا جاتا ہے جس کو آؤٹ پٹ گیٹ کہا جاتا ہے ، اور پھر خلیات کی حالت کو tanh پرت کے ذریعے جانا جاتا ہے تاکہ ایک ویکٹر حاصل کیا جاسکے جس کی قیمت -1 سے 1 کے درمیان ہے ، جس ویکٹر کو آؤٹ پٹ گیٹ کے ذریعہ حاصل کردہ فیصلے کی شرائط سے ضرب دیا جاتا ہے تاکہ حتمی RNN یونٹ کا آؤٹ پٹ مل سکے ، جیسا کہ ذیل میں دکھایا گیا ہے۔

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

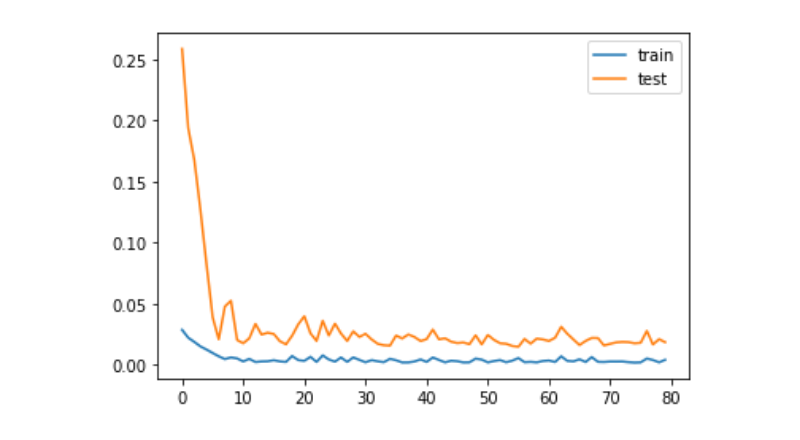
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

پیش گوئی

predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

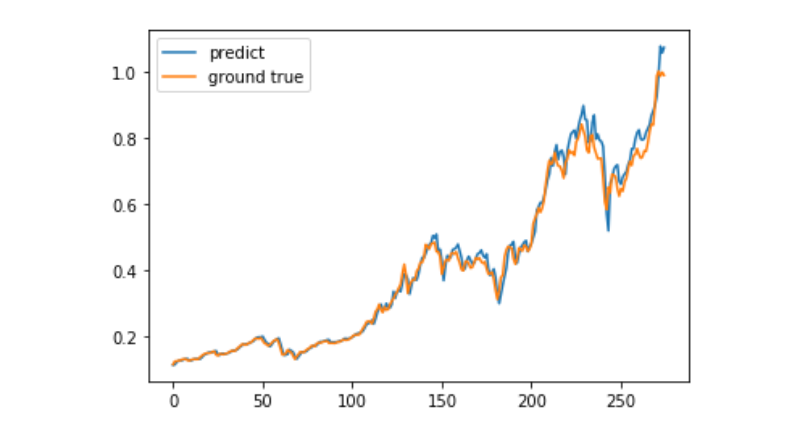
اس وقت مشین لرننگ کا استعمال کرتے ہوئے بٹ کوائن کی طویل مدتی قیمت کی پیش گوئی کرنا بہت مشکل ہے ، اس مضمون کو صرف سیکھنے کے معاملے کے طور پر استعمال کیا جاسکتا ہے۔ اس معاملے کو بعد میں آن لائن اور میٹرک پول کلاؤڈ کے ڈیمو آئینے میں لانچ کیا جائے گا ، جس میں دلچسپی رکھنے والے صارفین براہ راست تجربہ کرسکتے ہیں۔