پوشیدہ مارکوف ماڈل

• ### پہچاننا

آج ہم اسٹاک میں HMM کے سادہ اطلاق کے بارے میں بات کریں گے۔

مارکوف ماڈل کے بارے میں بات کرتے ہوئے ، یہ ایک اعلی درجے کی آواز ہے ، اور اس کے بارے میں کوئی اندازہ نہیں ہے ، تو آئیے ایک قدم پیچھے ہٹیں اور مارکوف چین کو دیکھیں۔

مارکوف چین ، جس کا نام آندرے مارکوف (A.A. Markov ، 1856-1922) کے نام پر رکھا گیا ہے ، ریاضی میں مارکوفی نوعیت کے مجرد واقعات کی بے ترتیب عمل کو ظاہر کرتا ہے۔ موجودہ علم یا معلومات کے معاملے میں ، ماضی (یعنی موجودہ سے پہلے کی تاریخی حالت) مستقبل کی پیش گوئی (یعنی موجودہ کے بعد کی مستقبل کی حالت) کے لئے بے معنی ہے۔

اس عمل میں، ہر ریاست کی منتقلی صرف پچھلی n ریاستوں پر منحصر ہوتی ہے، یہ عمل 1n درجے کے ماڈل کے نام سے جانا جاتا ہے، جہاں n منتقلی ریاستوں کی تعداد پر اثر انداز ہوتا ہے۔ سب سے آسان مارکوف عمل ایک درجے کا عمل ہے، ہر ریاست کی منتقلی صرف اس سے پہلے کی ریاست پر منحصر ہوتی ہے۔

• ### مثال دو

ریاضی کے اظہار سے یہ ظاہر ہوتا ہے کہ:

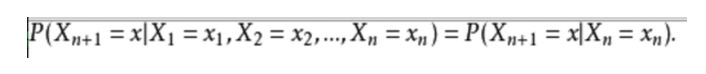
ایک مثال روزمرہ کی زندگی سے لیتا ہوں، ہم چاہتے ہیں کہ مستقبل کے موسم کی پیش گوئی موجودہ موسم کی صورت حال کی بنیاد پر کی جائے۔ ایک طریقہ یہ ہے کہ اس ماڈل کی ہر حالت کا انحصار صرف پچھلی حالت پر ہے، یعنی مارکوف کی مفروضہ، یہ مفروضہ اس مسئلے کو بہت حد تک آسان بنا دیتا ہے۔ یقیناً، یہ مثال بھی کچھ غیر عملی ہے۔ تاہم، اس طرح کا ایک آسان نظام ہمارے تجزیے میں فائدہ مند ثابت ہوسکتا ہے، اس لیے ہم عام طور پر اس طرح کے مفروضے کو قبول کرتے ہیں، کیونکہ ہم جانتے ہیں کہ ایسا نظام ہمیں کچھ مفید معلومات فراہم کر سکتا ہے، اگرچہ بہت درست نہیں ہے۔

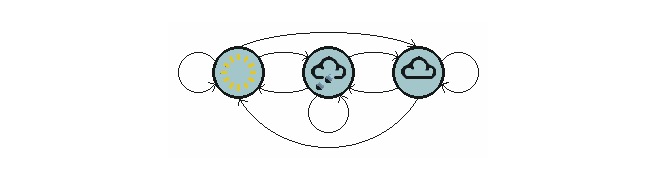
اوپر دی گئی تصویر میں موسم کی منتقلی کا ایک ماڈل دکھایا گیا ہے۔

نوٹ کریں کہ ایک مرحلے کا عمل جس میں N ریاستیں شامل ہیں اس میں N2 ریاستوں کی منتقلی ہوتی ہے۔ ہر منتقلی کا امکان ریاست کی منتقلی کا امکان کہا جاتا ہے ، یعنی ایک ریاست سے دوسری ریاست میں منتقلی کا امکان۔ ان تمام N2 امکانات کو ریاست کی منتقلی کے میٹرکس کے ذریعہ ظاہر کیا جاسکتا ہے ، جیسا کہ اوپر موسم کی مثال میں ریاست کی منتقلی کا میٹرکس ہے:

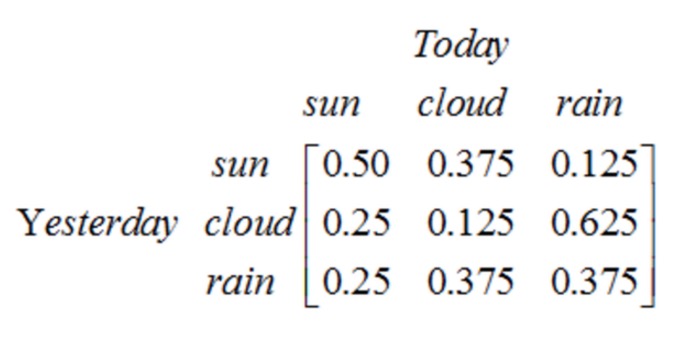
یہ میٹرکس بتاتا ہے کہ اگر کل ابر آلود تھا تو آج 25 فیصد امکان ہے کہ دن ہلکا ہو گا، 12.5 فیصد امکان ہے کہ یہ ابر آلود ہو گا، 62.5 فیصد امکان ہے کہ بارش ہو گی۔ واضح طور پر، میٹرکس میں ہر سطر کا مجموعہ 1 ≠ 1 ہے۔

اس طرح کے نظام کو شروع کرنے کے لئے، ہمیں ایک ابتدائی امکانات ویکٹر کی ضرورت ہے:

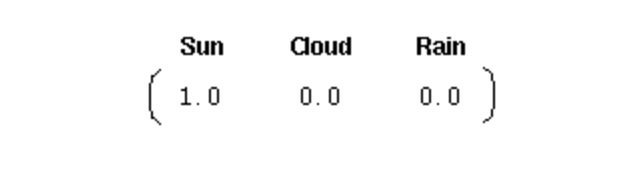
اس ویکٹر سے پتہ چلتا ہے کہ پہلا دن دن کا دن تھا۔ یہاں ، ہم نے مندرجہ ذیل تین حصوں کو اوپر والے مارکوف کے عمل کے لئے بیان کیا ہے:

اسٹیٹس: دھوپ، بادل اور بارش۔

ابتدائی ویکٹر: نظام کی حالت کا تعین کرنے کا امکان جب وقت 0 ہو۔

ریاست کی منتقلی کی میٹرکس: ہر قسم کے موسم کی منتقلی کا امکان۔ تمام نظام جو اس طرح بیان کیے جا سکتے ہیں وہ ایک مارکوف عمل ہے۔

تاہم ، جب مارکوف کا عمل کافی مضبوط نہیں ہوتا ہے تو ہم کیا کریں؟ کچھ معاملات میں ، مارکوف کا عمل ان نمونوں کی وضاحت کرنے کے لئے کافی نہیں ہے جو ہم تلاش کرنا چاہتے ہیں۔

مثال کے طور پر ہمارے اسٹاک مارکیٹ ، اگر صرف مارکیٹ کا مشاہدہ کیا جائے ، تو ہمیں صرف اس دن کی قیمت ، لین دین وغیرہ کی معلومات معلوم ہوسکتی ہے ، لیکن یہ نہیں معلوم کہ اسٹاک مارکیٹ اس وقت کس حالت میں ہے ((بیل مارکیٹ ، ریچھ مارکیٹ ، جھٹکا ، ریبوبل وغیرہ) ، اس معاملے میں ہمارے پاس دو ریاستوں کا مجموعہ ہے ، ایک قابل مشاہدہ ریاست کا مجموعہ ((اسٹاک مارکیٹ کی قیمتوں میں لین دین کی حالت وغیرہ) اور ایک پوشیدہ ریاست کا مجموعہ ((اسٹاک مارکیٹ کی حالت) ۔ ہم ایک ایسا الگورتھم تلاش کرنے کی امید کرتے ہیں جو اسٹاک مارکیٹ کی قیمتوں اور لین دین کی حالت اور مارکوف کے مفروضے پر مبنی اسٹاک مارکیٹ کی حالت کی پیش گوئی کرے گا۔

مذکورہ بالا حالات میں، مشاہدہ کی جانے والی ریاستوں کی سیریز اور پوشیدہ ریاستوں کی سیریز امکانات سے متعلق ہیں۔ اس طرح ہم اس قسم کے عمل کو ایک پوشیدہ مارکوف عمل اور اس پوشیدہ مارکوف عمل کے امکانات سے متعلق اور مشاہدہ کی جانے والی ریاستوں کے ایک مجموعہ کے طور پر ماڈل کرسکتے ہیں ، یعنی پوشیدہ مارکوف ماڈل۔

پوشیدہ مارکوف ماڈل (انگریزی: Hidden Markov Model) ایک شماریاتی ماڈل ہے جس کا استعمال مارکوف کے عمل کو بیان کرنے کے لیے کیا جاتا ہے جس میں پوشیدہ نامعلوم پیرامیٹرز شامل ہیں۔ اس کی مشکل یہ ہے کہ مشاہدہ کی جانے والی پیرامیٹرز میں سے اس عمل کے پوشیدہ پیرامیٹرز کا تعین کیا جائے اور پھر ان پیرامیٹرز کو مزید تجزیہ کے لیے استعمال کیا جائے۔ ذیل میں ایک تین ریاستوں کا پوشیدہ مارکوف ماڈل اسٹیٹ ٹرانسفر گراف ہے، جس میں x پوشیدہ ریاست ہے، y مشاہدہ کی جانے والی پیداوار ہے، a اسٹیٹ ٹرانسفر کا امکان ہے اور b پیداوار کا امکان ہے۔

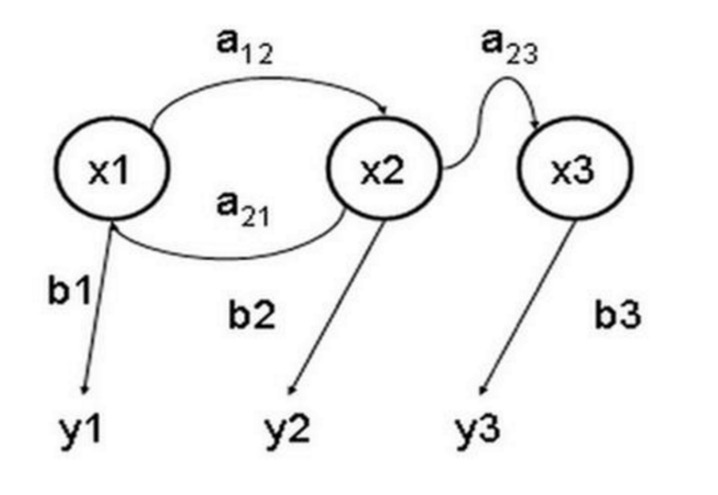
اس کی وضاحت کرنے کے لئے ، میں نے ایک جوتے کی مثال دی ہے۔ فرض کریں کہ میرے ہاتھ میں تین مختلف جوتے ہیں۔ پہلا جوتا ہمارا عام جوتا ہے ((اس جوتے کو D6 کہتے ہیں) ، جس کے 6 رخ ہیں ، ہر رخ ((1 ، 2 ، 3 ، 4 ، 5 ، 6) ظاہر ہونے کا امکان ¹⁄₆ ہے۔ دوسرا جوتا ایک چوتھائی ہے ((اس جوتے کو D4 کہتے ہیں) ، اور ہر رخ 1 ، ((2 ، 3 ، 4) ظاہر ہونے کا امکان ¹⁄₄ ہے۔ تیسرا جوتا آٹھ رخا ہے ((اس جوتے کو D8 کہتے ہیں)) ، اور ہر رخ ((1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 7 ، 8) ظاہر ہونے کا امکان ¹⁄₈ ہے۔

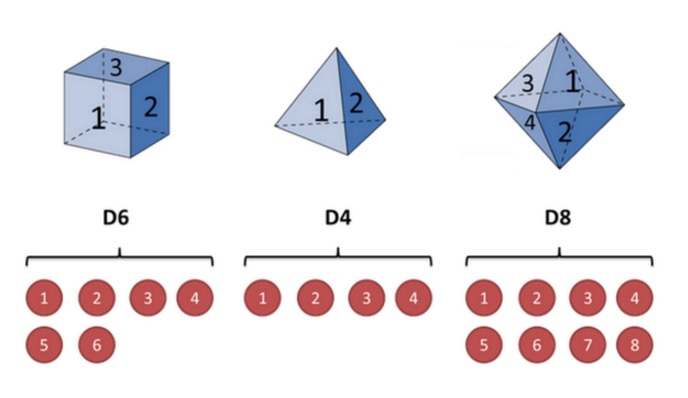
فرض کریں کہ ہم نے تین میں سے ایک کو منتخب کیا ہے اور اس کا امکان ¹⁄₃ ہے۔ پھر ہم نے ایک نمبر کو منتخب کیا ہے، ایک، دو، تین، چار، پانچ، چھ، سات، آٹھ میں سے ایک۔ اس عمل کو بار بار دہرائیں، اور ہمیں ایک نمبر مل جائے گا، ہر نمبر ایک، دو، تین، چار، پانچ، چھ، سات، آٹھ میں سے ایک ہے۔ مثال کے طور پر، ہمیں ایک نمبر مل سکتا ہے، دس بار۔

اس نمبر کی سٹرنگ کو ظاہر حالت کا سلسلہ کہا جاتا ہے۔ لیکن مارکوف کے خفیہ ماڈل میں ، ہمارے پاس نہ صرف یہ ظاہر حالت کا سلسلہ ہے ، بلکہ ایک پوشیدہ حالت کا سلسلہ بھی ہے۔ اس مثال میں ، پوشیدہ حالت کا سلسلہ آپ کے استعمال کردہ جوتے کی ترتیب ہے۔ مثال کے طور پر ، پوشیدہ حالت کا سلسلہ ہوسکتا ہے: D4 D6 D8 D6 D4 D8 D6 D6 D4

عام طور پر ، ایچ ایم ایم میں کہا جاتا ہے کہ مارکوف چین اصل میں پوشیدہ ریاست کی زنجیر ہے ، کیونکہ پوشیدہ ریاستوں کے مابین تبادلوں کا امکان موجود ہے۔ ہماری مثال میں ، D6 کی اگلی ریاست D4 ، D6 ، D8 کا امکان ¹⁄₃ ہے۔ D4 ، D8 کی اگلی ریاست D4 ، D6 ، D8 کا تبادلوں کا امکان ¹⁄₃ ہے۔ یہ ترتیب شروع میں آسان ہونے کے لئے ہے ، لیکن ہم واقعی تبادلوں کا امکان کسی بھی طرح سے طے کرسکتے ہیں۔ مثال کے طور پر ، ہم اس طرح کی وضاحت کرسکتے ہیں کہ D6 کے پیچھے D4 نہیں ہوسکتا ہے ، D6 کے پیچھے D6 کا امکان 0.9 ہے ، D8 کا امکان 0.1 ہے۔

اسی طرح، اگرچہ ظاہر حالتوں کے مابین تبادلوں کا امکان نہیں ہے، لیکن پوشیدہ حالت اور ظاہر حالت کے مابین ایک امکان ہے جسے آؤٹ پٹ کا امکان کہا جاتا ہے۔ ہماری مثال کے طور پر، چھ رخا مٹکا ((D6) 1 پیدا کرنے کا آؤٹ پٹ امکان ¹⁄₆ ہے۔ 2، 3، 4، 5، 6 پیدا کرنے کا امکان بھی ¹⁄₆ ہے۔ ہم آؤٹ پٹ امکان کی دوسری تعریف بھی کر سکتے ہیں۔ مثال کے طور پر، میرے پاس ایک چھ رخا مٹکا ہے جو کیسینو کے ہاتھوں اور پیروں سے گزرتا ہے، 1 کا امکان زیادہ ہے، 1/2، 2، 3، 4، 5، 6 کا امکان ¹⁄₁₀ ہے۔

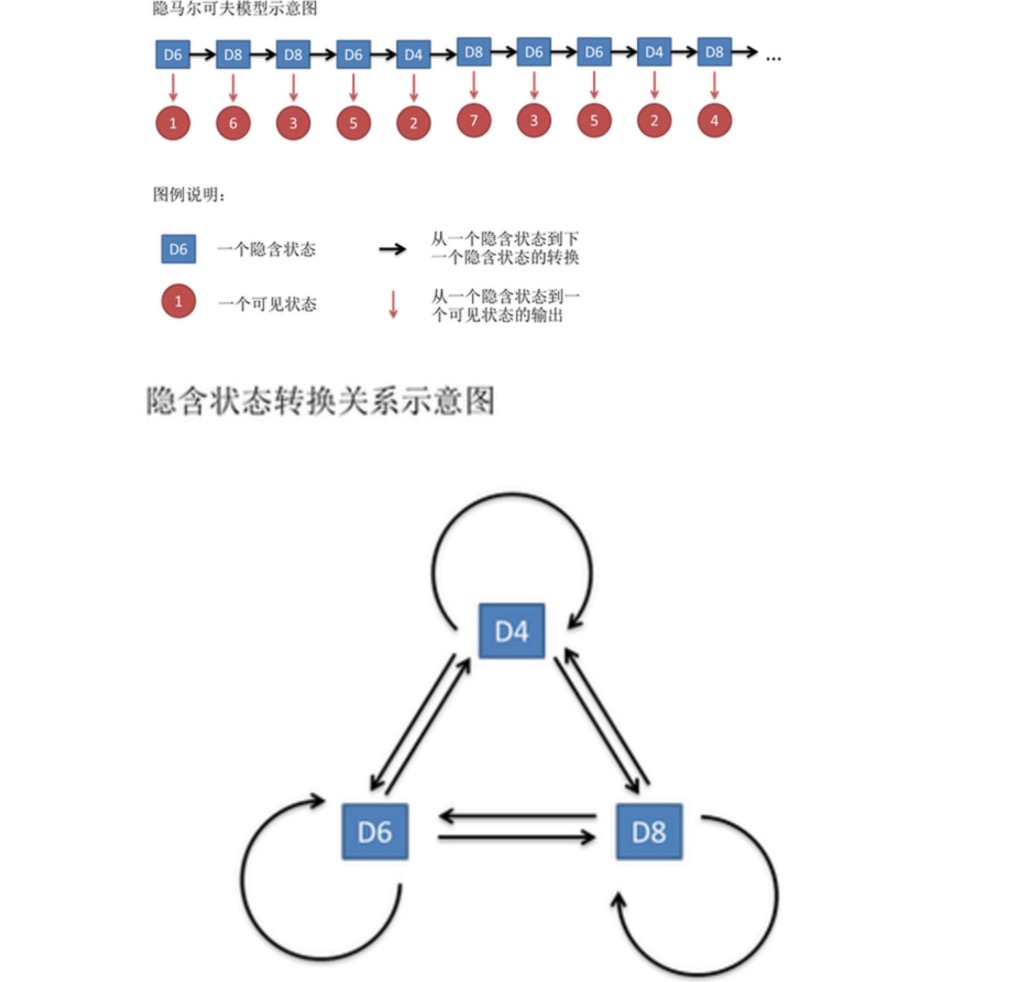
اصل میں ایچ ایم ایم کے لئے ، اگر آپ کو تمام پوشیدہ ریاستوں کے مابین تبادلوں کا امکان اور تمام پوشیدہ ریاستوں کے مابین تمام مرئی ریاستوں کے مابین آؤٹ پٹ کا امکان پہلے سے معلوم ہو تو ، تخروپن کرنا کافی آسان ہے۔ لیکن جب ایچ ایم ایم ماڈل کا اطلاق ہوتا ہے تو ، اکثر معلومات کا ایک حصہ غائب ہوتا ہے۔ بعض اوقات آپ کو معلوم ہوتا ہے کہ کتنے جوڑے ہیں ، ہر جوڑا کیا ہے ، لیکن آپ کو معلوم نہیں ہے کہ جوڑے کی ترتیب کیا ہے۔ بعض اوقات آپ صرف جوڑے کے نتائج کو کئی بار دیکھتے ہیں ، باقی کچھ نہیں جانتے ہیں۔ اگر آپ ان غائب معلومات کا اندازہ لگانے کے لئے الگورتھم کا اطلاق کرتے ہیں تو ، یہ ایک بہت اہم مسئلہ بن جاتا ہے۔

ایچ ایم ایم ماڈل سے متعلقہ الگورتھم بنیادی طور پر تین اقسام میں تقسیم ہوتے ہیں ، جن میں سے ہر ایک تین مسائل کو حل کرتا ہے:

• یہ جاننے کے لئے کہ کون سے جوڑے ہیں ((پوشیدہ ریاست کی تعداد) ، ہر جوڑا کیا ہے ((تبادلوں کا امکان) ، جو جوڑے کے نتائج کے مطابق (دیکھنے والی ریاست کا سلسلہ) ، میں جاننا چاہتا ہوں کہ ہر بار کون سا جوڑا نکالا جاتا ہے ((پوشیدہ ریاست کا سلسلہ)) ۔

• میں نے اس سوال کا جواب نہیں دیا ہے کہ کون سے حلقے کتنے ہیں؟ (بظاہر اسٹیٹس کی تعداد) ، ہر حلقے کا کیا مطلب ہے؟ (تبدیلی کا امکان) ، اور حلقے کے نتائج کے مطابق کیا ہوتا ہے؟ (بظاہر اسٹیٹس کا سلسلہ) ، میں اس نتیجے کے امکانات کو جاننا چاہتا ہوں۔

• یہ جاننے کے بعد کہ کون کون سے حلقے ہیں (((پوشیدہ ریاستوں کی تعداد) ، یہ جاننے کے بعد کہ کون کون سے حلقے ہیں (((تبدیلی کا امکان) ، بہت سے حلقوں کے نتائج کو دیکھنے کے بعد (((ظاہری ریاست کا سلسلہ) ، میں سوچتا ہوں کہ ہر حلقہ کیا ہے (((تبدیلی کا امکان)) ۔

  اگر ہم اسٹاک مارکیٹ کے مسائل کو حل کرنا چاہتے ہیں، تو ہمیں مسئلہ 1 اور مسئلہ 3 کو حل کرنے کی ضرورت ہے، اور اگلے مضمون میں ہم دیکھیں گے کہ یہ کیسے کریں.

ٹویٹ ایمبیڈ کریں