Cointegration کی بدیہی تفہیم

گائیڈ: اس مضمون کا مقصد ہم آہنگی کے تصور کو بصری طور پر متعارف کرانا ہے تاکہ آپ کو اس کے بنیادی معنی ، اس تصور کی حوصلہ افزائی اور اس کے استعمال کے آسان منظرناموں کو سمجھنے میں مدد ملے۔

• جامعہ کا تعارف

یہاں صرف یہ بتانے کی کوشش کی جارہی ہے کہ ہم آہنگی کی ایک بدیہی تعریف ہے ، اور اس میں ریاضی کے سخت علامات کی تعریف اور سخت فارمولے کی قیادت شامل نہیں ہے۔

اگر آپ دلچسپی رکھتے ہیں تو ، آپ کو ویکیپیڈیا کو انٹیگریشن دیکھنا چاہئے۔

ہم آہنگی کیوں؟

ہم آہنگی کے بارے میں بات کرتے ہوئے ، ہم آہنگی کا ذکر کرنا ضروری ہے۔

سادہ لفظوں میں ، استحکام (اسٹیشنریٹی) ایک ایسی خصوصیت ہے جس میں ایک سیریز وقت کے ساتھ مستحکم رہتی ہے ، یہ ایک ایسی خصوصیت ہے جو ہم اعداد و شمار کی تجزیاتی پیش گوئی کرتے وقت بہت پسند کرتے ہیں۔ اگر ٹائم سیریز کے اعداد و شمار کا ایک سیٹ مستحکم ہے تو ، اس کا مطلب یہ ہے کہ اس کی اوسط اور فرق کو برقرار رکھا گیا ہے ، لہذا ہم آسانی سے اس سلسلے میں کچھ شماریاتی تکنیک استعمال کرسکتے ہیں۔ آئیے پہلے ایک مثال پر نظر ڈالیں کہ مستحکم اور غیر مستحکم سیریز بصری طور پر کیسی نظر آتی ہیں۔

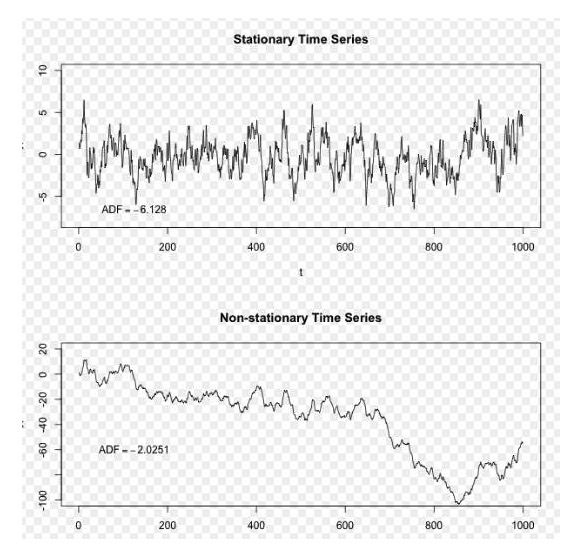
تصویر بشکریہ وکی پیڈیا

مندرجہ بالا تصویر میں، اوپر کی سیریز ایک مستحکم سیریز ہے، ہم دیکھ سکتے ہیں کہ یہ ہمیشہ ایک طویل مدتی اوسط کے ارد گرد اتار چڑھاؤ میں ہے، نیچے کی سیریز ایک غیر مستحکم سیریز ہے، ہم دیکھ سکتے ہیں کہ اس کی طویل مدتی اوسط متغیر ہے۔

ایک مثال کے طور پر ، اگر کسی اثاثہ کی قیمت کی ترتیب (یا دو سیریز کی قیمتوں کا فرق) مستحکم ہے ، تو جب اس کی اوسط قیمت سے انحراف ہوتا ہے تو ، ایک توقع کرسکتا ہے کہ قیمت مستقبل میں کسی وقت اس اوسط پر واپس آجائے گی۔ ہم اس خصوصیت سے سرمایہ کاری کرسکتے ہیں اور اس سے فائدہ اٹھاسکتے ہیں۔ فرض کریں کہ ایک اسٹاک کی طویل مدتی اوسط قیمت 9 ڈالر ہے ، اور اس کی موجودہ قیمت 8 ڈالر ہے۔ اگر جانچ پڑتال کے بعد ، ہم سمجھتے ہیں کہ اس اسٹاک کی تاریخی ترتیب مستحکم ہے ، اور فرض کریں کہ یہ استحکام برقرار رکھا جاسکتا ہے ، تو ہم اس اسٹاک کو خرید سکتے ہیں اور اس کے مستقبل کی قیمت 9 ڈالر پر واپس آنے کا انتظار کریں گے ، جس سے 1 ڈالر کا منافع ہوگا۔

اس کے علاوہ، یہ ایک اسٹاک کی قیمتوں کا ایک سلسلہ ہے جس کی ایک مستحکم نوعیت ہے:

استحکام بہت مفید ہے ، لیکن حقیقت میں ، زیادہ تر اسٹاک غیر مستحکم ہیں ، تو کیا ہم استحکام کی خصوصیات سے فائدہ اٹھا سکتے ہیں؟ اس کا جواب ہاں میں ہے ، اس وقت ہم آہنگی کا تعلق ہے ((cointegration))! اگر دو سیریز غیر مستحکم ہیں ، لیکن ان کے لکیری مجموعہ سے ہم آہنگی کا سلسلہ مل سکتا ہے ، تو ہم کہتے ہیں کہ دونوں سیریز کے اعداد و شمار کے اعداد و شمار میں ہم آہنگی کی خصوصیات ہیں ، ہم اس مجموعہ کی ترتیب پر بھی اعدادوشمار کی خصوصیات کا استعمال کرسکتے ہیں۔ لیکن یہ نوٹ کرنا ضروری ہے کہ ہم آہنگی کا تعلق تعلق نہیں ہے۔

مثال کے طور پر ، اگر ٹائم سیریز کے اعداد و شمار کے دو سیٹوں میں فرق مستحکم ہے تو ، ہم اس فرق کی استحکام کے مطابق سرمایہ کاری کر سکتے ہیں۔ جب دونوں اسٹاک کی قیمتوں میں فرق بہت زیادہ ہوتا ہے تو ، ہم استحکام کے مطابق قیمت کے فرق کو قریب لانے کی توقع کرتے ہیں ، لہذا کم قیمت والے اسٹاک خریدیں ، زیادہ قیمت والے اسٹاک کو بیچ دیں ، اور قیمت کی واپسی کا انتظار کرتے ہوئے منافع کمانے کے لئے ریورس آپریشن کریں۔

یہ جوڑی ٹریڈنگ کی اصل ہے۔ کیا یہ واضح ہے؟

• استحکام اور جانچ کے طریقے

سختی سے ، استحکام کو سختی سے اسٹیشنری اور کمزور استحکام (یا ہم آہنگی استحکام ، کوویاریئنس اسٹیشنری وغیرہ) میں تقسیم کیا جاسکتا ہے۔ سخت استحکام کا مطلب یہ ہے کہ ایک سیریز میں ہمیشہ مستقل تقسیم کی تقریب ہوتی ہے ، جبکہ کمزور استحکام کا مطلب یہ ہے کہ اس سیریز میں مستقل مستقل تعداد کی وضاحتی اعدادوشمار ہوتی ہے۔ تمام مضبوط مستحکم تسلسل کمزور استحکام کی خصوصیت کو پورا کرتے ہیں ، لیکن اس کے برعکس درست نہیں ہے۔ ہم جو استحکام کہتے ہیں وہ عام طور پر کمزور استحکام ہے۔ ٹائم سیریز کے تجزیے میں ، ہم عام طور پر یونٹ روٹ ٹیسٹ کے ذریعے فیصلہ کرتے ہیں کہ آیا کوئی عمل کمزور مستحکم ہے۔

مثال کے طور پر ایک ایپ

سب سے پہلے ، یہ نوٹ کرنا ضروری ہے کہ ہم آہنگی تعلقات متعلقہ تعلقات نہیں ہیں۔ ہم نے مصنوعی طور پر اعداد و شمار کے دو سیٹ بنائے ہیں ، لہذا ہم آہنگی تعلقات کو بصری طور پر دیکھ سکتے ہیں۔ import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

تعمیراتی اعداد و شمار

سب سے پہلے، ہم نے دو اعداد و شمار کے سیٹ تعمیر کیے ہیں، ہر ایک 100 اعداد و شمار کی لمبائی کے ساتھ. پہلے سیٹ میں 100 اعداد و شمار شامل ہیں، ایک نیچے کی طرف رجحانات کے ساتھ ساتھ ایک معیاری باقاعدہ تقسیم. دوسرا سیٹ اعداد و شمار کے پہلے سیٹ کے اعداد و شمار کی بنیاد پر 30، ایک اضافی معیاری باقاعدہ تقسیم کے ساتھ.

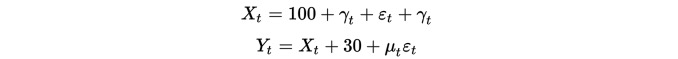
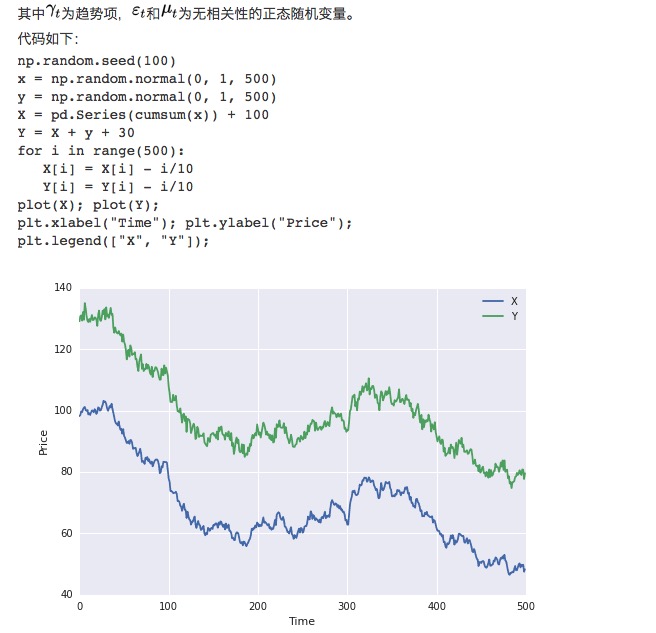
ظاہر ہے کہ اعداد و شمار کے دونوں سیٹ غیر مستحکم ہیں کیونکہ اوسط وقت کے ساتھ تبدیل ہوتا ہے۔ لیکن اعداد و شمار کے دونوں سیٹ مربوط ہیں کیونکہ ان کی فرق کی ترتیب مستحکم ہے:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

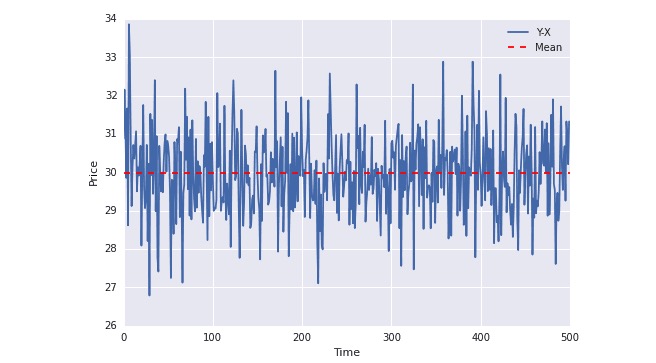
مندرجہ بالا گراف میں ، آپ دیکھ سکتے ہیں کہ نیلی لائن ہمیشہ اوسط کے ارد گرد اتار چڑھاؤ کرتی رہی ہے۔ اور اوسط وقت کے ساتھ نہیں بدلتی ہے (اصل میں ، اوسط بھی وقت کے ساتھ نہیں بدلتا ہے) ۔

• خلاصہ

اگر ہم ریاضی کے نقطہ نظر سے مکمل طور پر بات کرتے ہیں تو یہ پیچیدہ ہے ، اور اس میں مقداری کلاس شامل ہوگی۔ ہم نے صرف ایک سادہ تعارف کیا ہے جس کی سطح کو سمجھنے کے لئے ، تاکہ ہم انضمام کو عملی استعمال کے ساتھ بہتر طور پر جوڑ سکیں۔

آپ کے ساتھ اشتراک کرنے کے لئے، کوانٹم کلاس روم سے منتقل کریں