Python Naive Bayes ایپلی کیشن

بائیٹس کے نظریہ کے مطابق درجہ بندی کا یہ سادہ بیسٹ طریقہ حاصل کیا جاسکتا ہے، بشرطیکہ متغیرات ایک دوسرے سے آزاد ہوں۔ مزید آسان الفاظ میں، ایک سادہ بیسٹ درجہ بندی کرنے والا یہ فرض کرتا ہے کہ درجہ بندی کی ایک خصوصیت اس درجہ بندی کی دیگر خصوصیات سے غیر متعلق ہے۔ مثال کے طور پر، اگر ایک پھل گول اور سرخ ہے، اور اس کا قطر تقریبا 3 انچ ہے، تو یہ پھل شاید سیب ہے۔ اگرچہ یہ خصوصیات ایک دوسرے پر منحصر ہیں، یا دوسری خصوصیات پر منحصر ہیں، سادہ بیسٹ درجہ بندی کرنے والا یہ بھی فرض کرے گا کہ یہ خصوصیات انفرادی طور پر اس پھل کو ایک سیب کے طور پر اشارہ کرتی ہیں۔

• #### سادہ بیسٹ ماڈل تعمیر کرنے میں آسان ہے اور بڑے ڈیٹا سیٹ کے لئے بہت مفید ہے۔ اگرچہ یہ سادہ ہے ، لیکن سادہ بیسٹ کی کارکردگی انتہائی پیچیدہ درجہ بندی کے طریقوں سے کہیں زیادہ ہے۔

بیس کا نظریہ P (©) ، P ((x)) اور P ((x)) سے پتہ لگانے کا امکان P (©) کا حساب لگانے کا ایک طریقہ فراہم کرتا ہے۔ براہ کرم مندرجہ ذیل مساوات دیکھیں:

یہاں،

P (c < c < dx) ایک قسم کی (مقصد) کے بعد کے تجربے کا امکان ہے ، جس میں ایک متغیر (خاصیت) کی پیش گوئی کی جاتی ہے P (© کلاس کا سابقہ امکان ہے P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn Yksi) on todennäköisyys, joka ennakoi muuttujan tietyn luokan perusteella. P (x) پیش گوئی متغیر کی ابتدائی امکان ہے مثال: آئیے اس تصور کو ایک مثال کے ساتھ سمجھیں۔ ذیل میں ، میرے پاس موسم کے لئے ایک ٹریننگ سیٹ اور اس کے مطابق ہدف متغیر Play ہے۔ اب ، ہمیں موسم کے حالات کے مطابق کھیلنے والے اور نہ کھیلنے والے شرکاء کی درجہ بندی کرنے کی ضرورت ہے۔ آئیے مندرجہ ذیل اقدامات پر عمل کریں۔

مرحلہ 1: ڈیٹا سیٹ کو فریکوئینسی ٹیبل میں تبدیل کریں۔

مرحلہ 2: اس طرح کی ایک ٹیبل بنائیں جس میں 0.29 اوور کاسٹ کے امکان کے ساتھ 0.64 اوور کاسٹ کے امکان کا امکان ہو۔

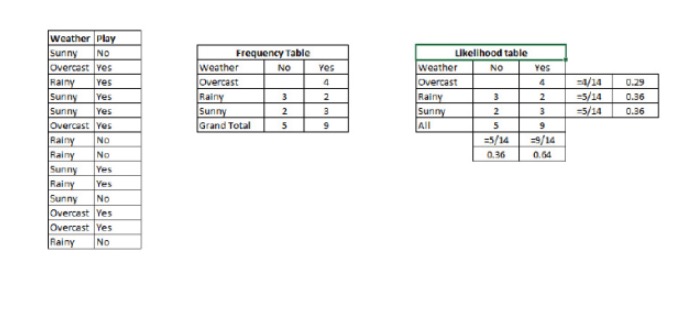
مرحلہ 3: اب ہم سادہ بیزس مساوات کا استعمال کرتے ہوئے ہر طبقے کے بعد کے امکانات کا حساب لگاتے ہیں۔ سب سے زیادہ بعد کے امکانات والے طبقے کی پیش گوئی کی جاتی ہے۔

سوال: کیا یہ بیان درست ہے؟ کیا آپ کو لگتا ہے کہ اس میں کوئی شک نہیں ہے کہ اگر موسم اچھا ہے تو کھلاڑی کھیل سکتے ہیں؟

ہم اس مسئلے کو حل کرنے کے لیے جو طریقہ ہم نے استعمال کیا ہے اس کا استعمال کر سکتے ہیں۔ تو P (کھیلتا ہے) = P (کھیلتا ہے) / P (کھیلتا ہے)

تو ہم نے P ہے ³⁄₉ 0.33, P ہے ⁵⁄₁₄ 0.36, P ہے ⁹⁄₁₄ 0.64.

اب، P{\displaystyle P} = 0.33 * 0.64 / 0.36 = 0.60، اور اس کا امکان زیادہ ہے۔

سادہ بیٹس نے ایک اسی طرح کا طریقہ استعمال کیا ہے جس میں مختلف صفات کے ذریعہ مختلف زمروں کی امکانات کی پیش گوئی کی جاتی ہے۔ یہ الگورتھم عام طور پر متن کی درجہ بندی کے لئے استعمال ہوتا ہے ، اور اس کے ساتھ ساتھ متعدد زمروں سے متعلق سوالات کے لئے بھی۔

• #### پیتھون کوڈ:

  #Import Library
  from sklearn.naive_bayes import GaussianNB
  　　
  #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) #Predict Output predicted= model.predict(x_test)