پچھلے ہفتے، ہم نے متعارف کرایاوی آر رسک مینجمنٹایک پورٹ فولیو کے خطرے کے بارے میں بات کرتے وقت، یہ ہر فرد کے اثاثے کے خطرے کے برابر نہیں ہے، لیکن ان کی قیمت کے ارتباط سے متعلق ہے۔ مثال کے طور پر دو اثاثوں کو لے کر، اگر ان کا مثبت ارتباط بہت مضبوط ہے، یعنی وہ ایک ساتھ اٹھتے اور گرتے ہیں، تو طویل سرمایہ کاری سے خطرہ کم نہیں ہوگا، اگر منفی تعلق بہت مضبوط ہے، تو تنوع خطرے کو نمایاں طور پر کم کر سکتا ہے۔ فطری سوال یہ ہے کہ جب کسی پورٹ فولیو میں سرمایہ کاری کرتے ہیں، تو آپ خطرے کی ایک مخصوص سطح پر منافع کو زیادہ سے زیادہ کیسے حاصل کرتے ہیں؟ یہ وہ جگہ ہے جہاں مارکووٹز تھیوری، جسے میں آج پیش کروں گا، عمل میں آتا ہے۔

جدید پورٹ فولیو تھیوری (MPT)، جو 1952 میں ہیری مارکووٹز نے تجویز کی تھی، پورٹ فولیو کے انتخاب کے لیے ایک ریاضیاتی فریم ورک ہے جس کا مقصد خطرات کو کنٹرول کرتے ہوئے مختلف پرخطر اثاثوں کے منافع کو منتخب کر کے متوقع منافع کو بڑھانا ہے۔ بنیادی خیال یہ ہے کہ اثاثوں کی قیمتیں کامل ہم آہنگی میں منتقل نہیں ہوتی ہیں (یعنی اثاثوں کے درمیان ایک نامکمل تعلق ہے)، اور مجموعی سرمایہ کاری کے خطرے کو اثاثوں کی تقسیم کو متنوع بنا کر کم کیا جا سکتا ہے۔

مارکووٹز تھیوری کے کلیدی تصورات

1. واپسی کی متوقع شرح: یہ وہ منافع ہے جو ایک سرمایہ کار اثاثہ یا پورٹ فولیو رکھ کر کمانے کی توقع کر سکتا ہے، عام طور پر تاریخی واپسی کے اعداد و شمار کی بنیاد پر پیش گوئی کی جاتی ہے۔

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

جہاں \(E(R_p)\) پورٹ فولیو کی واپسی کی متوقع شرح ہے، \(wi\) پورٹ فولیو میں \(i\)th اثاثہ کا وزن ہے، اور \(E(R_i)\) \( کی واپسی کی متوقع شرح ہے۔ i\)th اثاثہ.

1. خطرہ ( اتار چڑھاؤ یا معیاری انحراف): سرمایہ کاری کے منافع کی غیر یقینی صورتحال یا سرمایہ کاری کے اتار چڑھاؤ کی پیمائش کے لیے استعمال کیا جاتا ہے۔

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

جہاں \(\sigma_p\) پورٹ فولیو کا کل خطرہ ہے اور \(\sigma_{ij}\) اثاثہ \(i\) اور اثاثہ \(j\) کے درمیان ہم آہنگی ہے، جو دو اثاثوں کی قیمتوں میں ہونے والی تبدیلیوں کے درمیان تعلق کی پیمائش کرتا ہے۔

1. ہم آہنگی: دو اثاثوں کی قیمت کی نقل و حرکت کے درمیان ارتباط کی پیمائش کرتا ہے۔

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

جہاں \(\rho_{ij}\) اثاثہ \(i\) اور اثاثہ \(j\) کے درمیان ارتباط کا گتانک ہے، \(\sigma_i\) اور \(\sigma_j\) بالترتیب اثاثہ \(i\) اور اثاثہ \(j\) کے معیاری انحراف ہیں۔

1. موثر فرنٹیئر: رسک ریٹرن کوآرڈینیٹ سسٹم میں، موثر فرنٹیئر پورٹ فولیوز کا وہ سیٹ ہے جو کسی مخصوص خطرے کی سطح پر زیادہ سے زیادہ متوقع واپسی فراہم کر سکتا ہے۔

اوپر دی گئی تصویر مؤثر فرنٹیئر کا ایک سکیمیٹک ڈایاگرام ہے جس میں مختلف وزن کے ساتھ افقی محور ہے، یعنی خطرے کی سطح، اور عمودی محور واپسی کی شرح ہے۔ ظاہر ہے، ہم گراف کے اوپری کنارے پر توجہ مرکوز کرتے ہیں، جو اسی خطرے کی سطح پر سب سے زیادہ منافع حاصل کرتا ہے۔

مقداری تجارت اور پورٹ فولیو کے انتظام میں، ان اصولوں کو لاگو کرنے کے لیے تاریخی اعداد و شمار کے شماریاتی تجزیہ اور متوقع منافع، معیاری انحراف اور مختلف اثاثوں کے ہم آہنگی کا تخمینہ لگانے کے لیے ریاضیاتی ماڈلز کے استعمال کی ضرورت ہوتی ہے۔ پھر، بہترین اثاثہ وزن کی ترتیب کو تلاش کرنے کے لیے اصلاح کی تکنیکوں کا اطلاق کیا جاتا ہے۔ اس عمل میں عام طور پر پیچیدہ ریاضیاتی حسابات اور بہت ساری کمپیوٹر پروسیسنگ شامل ہوتی ہے، یہی وجہ ہے کہ جدید مالیات میں مقداری تجزیہ بہت اہم ہو گیا ہے۔ مندرجہ ذیل ایک مخصوص ازگر کی مثال استعمال کرے گا تاکہ یہ واضح کیا جا سکے کہ کس طرح بہتر بنایا جائے۔

تخروپن کا طریقہ استعمال کرتے ہوئے بہترین امتزاج تلاش کرنے کے لیے ازگر کوڈ کی مثال

مارکووٹز کے بہترین پورٹ فولیو کا حساب لگانا ایک کثیر مرحلہ عمل ہے جس میں ڈیٹا کی تیاری، پورٹ فولیو سمولیشن، اور اشارے کا حساب جیسے کئی اہم مراحل شامل ہیں۔ حوالہ: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. مارکیٹ ڈیٹا حاصل کریں۔：

   • پاسget_dataمنتخب ڈیجیٹل کرنسی کی تاریخی قیمت کا ڈیٹا حاصل کرنے کا فنکشن۔ یہ وہ ڈیٹا ہے جو واپسی اور خطرے کی شرح کا حساب لگانے کے لیے ضروری ہے، جو پورٹ فولیوز بنانے اور تیز تناسب کا حساب لگانے کے لیے استعمال ہوتے ہیں۔

2. واپسی اور رسک کا حساب لگانا：

   • استعمال کریںcalculate_returns_riskفنکشن ہر ڈیجیٹل کرنسی کے لیے سالانہ شرح منافع اور سالانہ خطرے (معیاری انحراف) کا حساب لگاتا ہے۔ یہ ایک بہترین پورٹ فولیو میں استعمال کرنے کے لیے ہر اثاثہ کی تاریخی کارکردگی کا اندازہ لگانا ہے۔

3. مارکووٹز کے بہترین پورٹ فولیو کا حساب لگائیں۔：

   • استعمال کریںcalculate_optimal_portfolioفنکشن، ایک سے زیادہ پورٹ فولیوز کی نقالی۔ ہر ایک سمولیشن میں، اثاثے کے وزن تصادفی طور پر تیار کیے جاتے ہیں اور پورٹ فولیو کی متوقع واپسی اور خطرے کا حساب ان وزنوں کی بنیاد پر کیا جاتا ہے۔
   • تصادفی طور پر مختلف وزنوں کے امتزاج پیدا کرنے سے، بہترین امتزاج تلاش کرنے کے لیے متعدد ممکنہ پورٹ فولیوز کو تلاش کیا جا سکتا ہے۔ یہ مارکووٹز کے پورٹ فولیو تھیوری کے بنیادی خیالات میں سے ایک ہے۔

اس پورے عمل کا مقصد اس پورٹ فولیو کو تلاش کرنا ہے جو خطرے کی دی گئی سطح کے لیے بہترین متوقع واپسی دیتا ہے۔ متعدد ممکنہ امتزاج کی تقلید کرکے، سرمایہ کار بہتر طور پر سمجھ سکتے ہیں کہ مختلف کنفیگریشنز کس طرح کارکردگی کا مظاہرہ کریں گی اور اس امتزاج کا انتخاب کریں جو ان کے سرمایہ کاری کے مقاصد اور خطرے کی رواداری کے لیے بہترین ہو۔ یہ نقطہ نظر سرمایہ کاری کے فیصلوں کو بہتر بنانے اور سرمایہ کاری کو زیادہ موثر بنانے میں مدد کرتا ہے۔

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
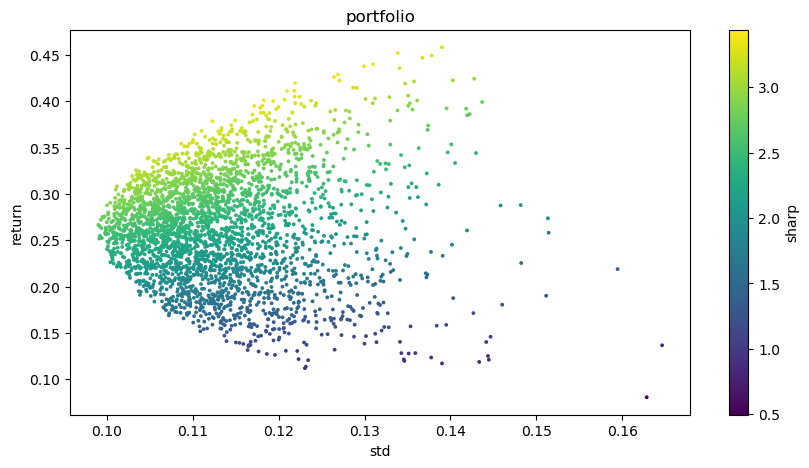
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

حتمی پیداوار: بہترین امتزاج: BTCUSDT وزن: 0.0721 ETHUSDT وزن: 0.2704 BNBUSDT وزن: 0.3646 LINKUSDT وزن: 0.1892 BCHUSDT وزن: 0.0829 LTCUSDT وزن: 0.0209 متوقع واپسی: 0.4195 متوقع خطرہ (معیاری انحراف): 0.1219 تیز تناسب: 3.4403