اے آر ایم اے-ایگارچ ماڈل پر مبنی بٹ کوائن کی اتار چڑھاؤ کا ماڈلنگ اور تجزیہ

حال ہی میں ، میں نے بٹ کوائن کی اتار چڑھاؤ پر کچھ تجزیہ کیا ہے ، جو لفظی اور خود بخود ہے۔ لہذا میں صرف اپنی کچھ تفہیم اور کوڈ کو مندرجہ ذیل طور پر بانٹتا ہوں۔ میری صلاحیت محدود ہے ، اور کوڈ بہت کامل نہیں ہے۔ اگر کوئی غلطی ہے تو ، براہ کرم اس کی نشاندہی کریں اور اسے براہ راست درست کریں۔

1۔ فنانس کی ٹائم سیریز کا مختصر بیان

فنانس کی ٹائم سیریز اسٹوکاسٹک پروسیس سیریز ماڈلز کا ایک مجموعہ ہے جو وقت کی جہت میں مشاہدہ کردہ متغیر پر مبنی ہے۔ متغیر عام طور پر اثاثوں کی واپسی کی شرح ہوتا ہے۔ چونکہ واپسی کی شرح سرمایہ کاری کے پیمانے سے آزاد ہے اور اس کی شماریاتی نوعیت ہے ، لہذا بنیادی مالیاتی اثاثوں کے سرمایہ کاری کے مواقع کا تجزیہ کرنا زیادہ قیمتی ہے۔

یہاں ، یہ دلیری سے فرض کیا جاتا ہے کہ بٹ کوائن کی واپسی کی شرح عام مالیاتی اثاثوں کی واپسی کی شرح کی خصوصیات کے مطابق ہے ، یعنی ، یہ ایک کمزور ہموار سلسلہ ہے ، جس کا مظاہرہ متعدد نمونوں کے مستقل مزاجی ٹیسٹ کے ذریعہ کیا جاسکتا ہے۔

1-1. تیاریاں، درآمد لائبریریاں، انکیپسول افعال

ریسرچ ماحول کی تشکیل مکمل ہے۔ بعد کے حساب کتاب کے لئے درکار لائبریری یہاں درآمد کی گئی ہے۔ چونکہ یہ وقفے وقفے سے لکھی جاتی ہے ، لہذا یہ ضرورت سے زیادہ ہوسکتی ہے۔ براہ کرم اسے خود صاف کریں۔

میں [1]:

'''
start: 2020-02-01 00:00:00
end: 2020-03-01 00:00:00
period: 1h
exchanges: [{"eid":"Huobi","currency":"BTC_USDT","stocks":0}]
'''
from __future__ import absolute_import, division, print_function
from fmz import * # Import all FMZ functions
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from statsmodels.graphics.api import qqplot
from statsmodels.stats.diagnostic import acorr_ljungbox as lb_test
from scipy import stats
from arch import arch_model
from datetime import timedelta
from itertools import product
from math import sqrt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error

task = VCtx(__doc__) # Initialization, verification of FMZ reading of historical data
print(exchange.GetAccount())

باہر[1]: {توازن: 10000.0، منجمد توازن: 0.0، اسٹاک: 0.0، منجمد اسٹاک: 0.0}

    #### Encapsulate some of the functions, which will be used later. If there is a source, see the note

[17] میں:

# Plot functions
def tsplot(y, y_2, lags=None, title='', figsize=(18, 8)):  # source code: https://tomaugspurger.github.io/modern-7-timeseries.html
    fig = plt.figure(figsize=figsize)
    layout = (2, 2)
    ts_ax   = plt.subplot2grid(layout, (0, 0))
    ts2_ax = plt.subplot2grid(layout, (0, 1))
    acf_ax  = plt.subplot2grid(layout, (1, 0))
    pacf_ax = plt.subplot2grid(layout, (1, 1))
    y.plot(ax=ts_ax)
    ts_ax.set_title(title)
    y_2.plot(ax=ts2_ax)
    smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
    smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
    [ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
    sns.despine()
    plt.tight_layout()
    return ts_ax, ts2_ax, acf_ax, pacf_ax

# Performance evaluation
def get_rmse(y, y_hat):
    mse = np.mean((y - y_hat)**2)
    return np.sqrt(mse)

def get_mape(y, y_hat):
    perc_err = (100*(y - y_hat))/y
    return np.mean(abs(perc_err))

def get_mase(y, y_hat):
    abs_err = abs(y - y_hat)
    dsum=sum(abs(y[1:] - y_hat[1:]))
    t = len(y)
    denom = (1/(t - 1))* dsum
    return np.mean(abs_err/denom)

def mae(observation, forecast):    
    error = mean_absolute_error(observation, forecast)
    print('Mean Absolute Error (MAE): {:.3g}'.format(error))
    return error

def mape(observation, forecast): 
    observation, forecast = np.array(observation), np.array(forecast)
    # Might encounter division by zero error when observation is zero
    error = np.mean(np.abs((observation - forecast) / observation)) * 100
    print('Mean Absolute Percentage Error (MAPE): {:.3g}'.format(error))
    return error

def rmse(observation, forecast):
    error = sqrt(mean_squared_error(observation, forecast))
    print('Root Mean Square Error (RMSE): {:.3g}'.format(error))
    return error

def evaluate(pd_dataframe, observation, forecast):
    first_valid_date = pd_dataframe[forecast].first_valid_index()
    mae_error = mae(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    mape_error = mape(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ])
    rmse_error = rmse(pd_dataframe[observation].loc[first_valid_date:, ], pd_dataframe[forecast].loc[first_valid_date:, ]) 

    ax = pd_dataframe.loc[:, [observation, forecast]].plot(figsize=(18,5))
    ax.xaxis.label.set_visible(False)
    return

1-2۔ آئیے بٹ کوائن کے تاریخی اعداد و شمار کی مختصر تفہیم کے ساتھ شروع کرتے ہیں

اعدادوشمار کے نقطہ نظر سے ، ہم بٹ کوائن کی کچھ ڈیٹا خصوصیات پر ایک نظر ڈال سکتے ہیں۔ گذشتہ سال کی ڈیٹا کی تفصیل کو مثال کے طور پر لیتے ہوئے ، واپسی کی شرح کا حساب آسان طریقے سے کیا جاتا ہے ، یعنی اختتامی قیمت کو لوگرتھمک طور پر گھٹا دیا جاتا ہے۔ فارمولا مندرجہ ذیل ہے: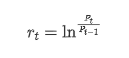

میں [3]:

df = get_bars('huobi.btc_usdt', '1d', count=10000, start='2019-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
mean = btc_year_test.mean()
std = btc_year_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value'], columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% btc_year_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% btc_year_test.kurt())
normal_result

آؤٹ [1]: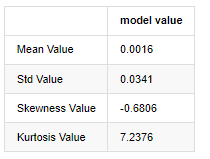

موٹی چربی کی دم کی خصوصیت یہ ہے کہ وقت کا پیمانہ جتنا مختصر ہوگا ، خصوصیت اتنی ہی اہم ہوگی۔ ڈیٹا کی تعدد میں اضافے کے ساتھ کورٹوسس میں اضافہ ہوگا ، اور یہ خصوصیت اعلی تعدد کے ڈیٹا میں بہت واضح ہوگی۔

یکم جنوری 2019 سے لے کر آج تک کی روزانہ بندش کی قیمت کے اعداد و شمار کو بطور مثال لیتے ہوئے ، ہم اس کی لوگرتھمک واپسی کی شرح کا وضاحتی تجزیہ کرتے ہیں ، اور یہ دیکھا جاسکتا ہے کہ بٹ کوائن کی سادہ واپسی کی شرح سیریز معمول کی تقسیم کے مطابق نہیں ہے ، اور اس میں موٹی موٹی دم کی واضح خصوصیت ہے۔

ترتیب کی اوسط قیمت 0.0016 ہے ، معیاری انحراف 0.0341 ہے ، منحرفیت -0.6819 ہے ، اور کورٹوسس 7.2243 ہے ، جو عام تقسیم سے بہت زیادہ ہے اور اس میں موٹی چربی کی دم کی خصوصیت ہے۔ بٹ کوائن کی سادہ واپسی کی شرح کی معمول کو QQ چارٹ کے ذریعہ مندرجہ ذیل طریقے سے ماپا اور تجربہ کیا گیا ہے:

[4] میں:

fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(111)
fig = qqplot(btc_year_test['log_return'], line='q', ax=ax, fit=True)

آؤٹ [4]:

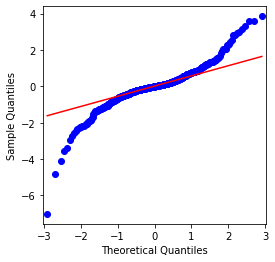
یہ دیکھا جاسکتا ہے کہ کیو کیو چارٹ کامل ہے ، اور بٹ کوائن کے لئے لوگرتھمک ریٹرن سیریز نتائج سے معمول کی تقسیم کے مطابق نہیں ہے ، اور اس میں موٹی موٹی دم کی واضح خصوصیت ہے۔

اگلا ، آئیے اتار چڑھاؤ کے مجموعی اثر پر ایک نظر ڈالیں ، یعنی مالی وقت کی سیریز اکثر زیادہ اتار چڑھاؤ کے بعد زیادہ اتار چڑھاؤ کے ساتھ ہوتی ہے ، جبکہ کم اتار چڑھاؤ عام طور پر کم اتار چڑھاؤ کے بعد ہوتا ہے۔

Volatility Clustering Volatility کے مثبت اور منفی فیڈ بیک اثرات کی عکاسی کرتا ہے اور یہ چربی کی دم کی خصوصیات کے ساتھ انتہائی وابستہ ہے۔ معاشی لحاظ سے ، اس کا مطلب یہ ہے کہ اتار چڑھاؤ کی ٹائم سیریز خود بخود وابستہ ہوسکتی ہے ، یعنی موجودہ مدت کی اتار چڑھاؤ کا پچھلی مدت ، دوسری پچھلی مدت ، یا یہاں تک کہ تیسری پچھلی مدت سے کچھ تعلق ہوسکتا ہے۔

میں [5]:

df = get_bars('huobi.btc_usdt', '1d', count=50000, start='2006-01-01')
btc_year = pd.DataFrame(df['close'],dtype=np.float)
btc_year.index.name = 'date'
btc_year.index = pd.to_datetime(btc_year.index)
btc_year['log_price'] = np.log(btc_year['close'])
btc_year['log_return'] = btc_year['log_price'] - btc_year['log_price'].shift(1)
btc_year['log_return_100x'] = np.multiply(btc_year['log_return'], 100)

btc_year_test = pd.DataFrame(btc_year['log_return'].dropna(), dtype=np.float)
btc_year_test.index.name = 'date'
sns.mpl.rcParams['figure.figsize'] = (18, 4)  # Volatility
ax1 = btc_year_test['log_return'].plot()
ax1.xaxis.label.set_visible(False)

باہر[5]:

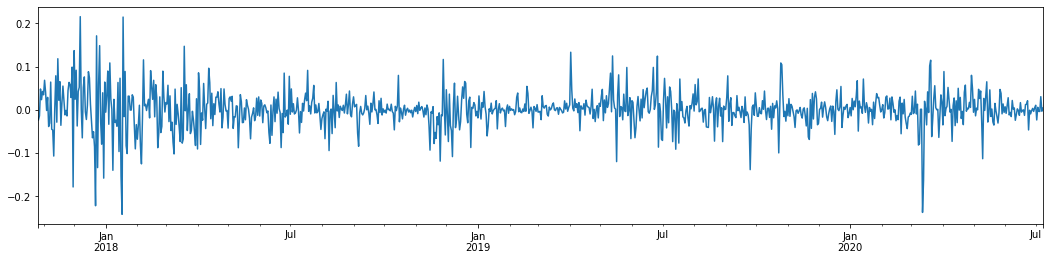
پچھلے 3 سالوں میں بٹ کوائن کی روزانہ لاگرتھمک شرح واپسی کو لے کر اور اس کا خاکہ پیش کرتے ہوئے ، اتار چڑھاؤ کے گروپوں کا رجحان واضح طور پر دیکھا جاسکتا ہے۔ 2018 میں بٹ کوائن میں بیل مارکیٹ کے بعد ، یہ زیادہ تر وقت مستحکم موقف میں رہا۔ جیسا کہ ہم دائیں طرف دیکھ سکتے ہیں ، مارچ 2020 میں ، جب عالمی مالیاتی منڈیوں میں گراوٹ آئی ، تو بٹ کوائن لیکویڈیٹی پر بھی ایک رن تھا ، جس میں پیداوار ایک دن میں تقریبا 40 فیصد گر گئی ، تیز منفی جھولوں کے ساتھ۔

ایک لفظ میں ، بدیہی مشاہدے سے ، ہم دیکھ سکتے ہیں کہ ایک بڑی اتار چڑھاؤ کے بعد ایک کثیف اتار چڑھاؤ آئے گا جس کا امکان بہت زیادہ ہے ، جو اتار چڑھاؤ کا مجموعی اثر بھی ہے۔ اگر یہ اتار چڑھاؤ کی حد متوقع ہے تو ، یہ بی ٹی سی کے قلیل مدتی لین دین کے لئے قیمتی ہے ، جو اتار چڑھاؤ پر تبادلہ خیال کرنے کا مقصد بھی ہے۔

1-3. ڈیٹا کی تیاری

ٹریننگ نمونہ سیٹ تیار کرنے کے لئے ، پہلے ، ہم ایک بینچ مارک نمونہ قائم کرتے ہیں ، جس میں لاگارتھمک ریٹرن کی شرح مساوی مشاہدہ شدہ اتار چڑھاؤ ہے۔ چونکہ دن کی اتار چڑھاؤ کو براہ راست مشاہدہ نہیں کیا جاسکتا ہے ، لہذا گھنٹے کے اعداد و شمار کو دوبارہ نمونے لینے کے لئے استعمال کیا جاتا ہے تاکہ دن کی حقیقت میں اتار چڑھاؤ کا نتیجہ اخذ کیا جاسکے اور اسے اتار چڑھاؤ کے منحصر متغیر کے طور پر لیا جاسکے۔

دوبارہ نمونے لینے کا طریقہ گھنٹوں کے اعداد و شمار پر مبنی ہے۔ فارمولا مندرجہ ذیل ہے: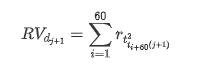

[4] میں:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_all = pd.DataFrame(df['close'], dtype=np.float)
kline_all.index.name = 'date'
kline_all['log_price'] = np.log(kline_all['close'])  # Calculate daily logarithmic rate of return
kline_all['return'] = kline_all['log_price'].pct_change().dropna()
kline_all['log_return'] = kline_all['log_price'] - kline_all['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_all['squared_log_return'] = np.power(kline_all['log_return'], 2)  # The exponential square of logarithmic daily rate of return

kline_all['return_100x'] = np.multiply(kline_all['return'], 100)
kline_all['log_return_100x'] = np.multiply(kline_all['log_return'], 100)  # Enlarge 100 times

kline_all['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy()  # Resampling to days
kline_all['realized_volatility_1_hour'] = np.sqrt(kline_all['realized_variance_1_hour'])  # Volatility of variance derivation

kline_all = kline_all[4:-29] # Remove the last line because it is missing
kline_all.head(3)

آؤٹ [4]: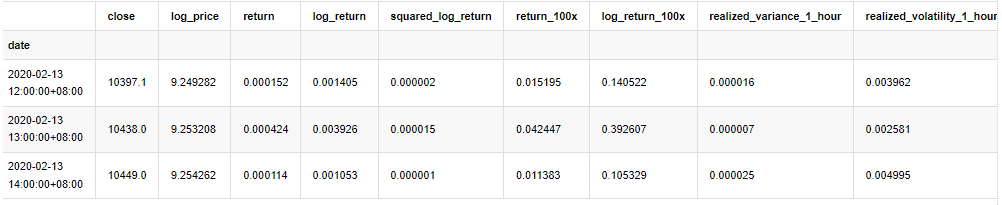

نمونہ کے باہر کے اعداد و شمار کو اسی طرح تیار کریں

میں [5]:

# Prepare the data outside the sample with realized daily volatility
df = get_bars('huobi.btc_usdt', '1m', count=50000, start='2020-02-13')  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times
kline_1m['squared_log_return'] = np.power(kline_1m['log_return_100x'], 2)
kline_1m#.tail()
df = get_bars('huobi.btc_usdt', '1h', count=860, start='2020-02-13')  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate daily logarithmic rate of return
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate logarithmic rate of return
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times
kline_test['squared_log_return'] = np.power(kline_test['log_return_100x'], 2)  # The exponential square of logarithmic daily rate of return
kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum()  # Resampling to days
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation
kline_test = kline_test[4:-2]

نمونے کے بنیادی اعداد و شمار کو سمجھنے کے لئے، ایک سادہ وضاحتی تجزیہ مندرجہ ذیل طور پر کیا جاتا ہے:

[9] میں:

line_test = pd.DataFrame(kline_train['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'

mean = line_test.mean()  # Calculate mean value and standard deviation
std = line_test.std()

line_test.sort_values(by = 'log_return', inplace = True)  # Resort
s_r = line_test.reset_index(drop = False)  # After resorting, update index
s_r['p'] = (s_r.index - 0.5) / len(s_r)  # Calculate the percentile p(i)
s_r['q'] = (s_r['log_return'] - mean) / std  # Calculate the value of q

st = line_test.describe()
x1 ,y1 = 0.25, st['log_return']['25%']
x2 ,y2 = 0.75, st['log_return']['75%']

fig = plt.figure(figsize = (18,8))
layout = (2, 2)
ax1 = plt.subplot2grid(layout, (0, 0), colspan=2)# Plot the data distribution
ax2 = plt.subplot2grid(layout, (1, 0))# Plot histogram
ax3 = plt.subplot2grid(layout, (1, 1))# Draw the QQ chart, the straight line is the connection of the quarter digit, three-quarters digit, which is basically conforms to the normal distribution

ax1.scatter(line_test.index, line_test.values)
line_test.hist(bins=30,alpha = 0.5,ax = ax2)
line_test.plot(kind = 'kde', secondary_y=True,ax = ax2)
ax3.plot(s_r['p'],s_r['log_return'],'k.',alpha = 0.1)
ax3.plot([x1,x2],[y1,y2],'-r')
sns.despine()
plt.tight_layout()

آؤٹ [9]:

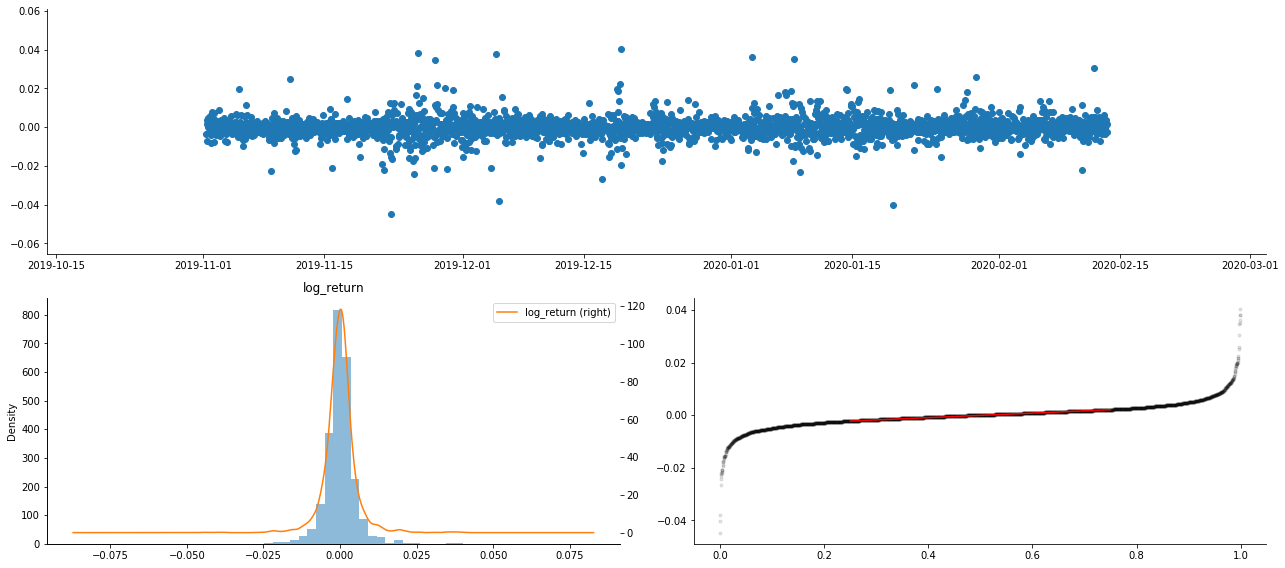
نتیجے کے طور پر، لوگرتھمک واپسی کے وقت سیریز چارٹ میں واضح اتار چڑھاؤ مجموعہ اور فائدہ اٹھانے کا اثر ہے.

لوگرتھمک واپسیوں کے تقسیم چارٹ میں مسخ 0 سے کم ہے ، جس سے یہ ظاہر ہوتا ہے کہ نمونے میں واپسی قدرے منفی اور دائیں طرف متوجہ ہے۔ لوگرتھمک واپسیوں کے QQ چارٹ میں ، ہم دیکھ سکتے ہیں کہ لوگرتھمک واپسیوں کی تقسیم نارمل نہیں ہے۔

اعداد و شمار کی تقسیم کا مسخ 1 سے کم ہے ، جس سے یہ ظاہر ہوتا ہے کہ نمونہ کے اندر واپسی قدرے مثبت اور قدرے دائیں طرف متوجہ ہے۔ کورٹوسس کی قیمت 3 سے زیادہ ہے ، جس سے یہ ظاہر ہوتا ہے کہ پیداوار موٹی چربی کی دم تقسیم ہے۔

اب جب ہم اس مقام پر پہنچ چکے ہیں، آئیے ایک اور شماریاتی ٹیسٹ کرتے ہیں۔ میں [7]:

line_test = pd.DataFrame(kline_all['log_return'].dropna(), dtype=np.float)
line_test.index.name = 'date'
mean = line_test.mean()
std = line_test.std()
normal_result = pd.DataFrame(index=['Mean Value', 'Std Value', 'Skewness Value','Kurtosis Value',
                                    'Ks Test Value','Ks Test P-value',
                                    'Jarque Bera Test','Jarque Bera Test P-value'],
                    columns=['model value'])
normal_result['model value']['Mean Value'] = ('%.4f'% mean[0])
normal_result['model value']['Std Value'] = ('%.4f'% std[0])
normal_result['model value']['Skewness Value'] = ('%.4f'% line_test.skew())
normal_result['model value']['Kurtosis Value'] = ('%.4f'% line_test.kurt())
normal_result['model value']['Ks Test Value'] = stats.kstest(line_test, 'norm', (mean, std))[0]
normal_result['model value']['Ks Test P-value'] = stats.kstest(line_test, 'norm', (mean, std))[1]
normal_result['model value']['Jarque Bera Test'] = stats.jarque_bera(line_test)[0]
normal_result['model value']['Jarque Bera Test P-value'] = stats.jarque_bera(line_test)[1]
normal_result

آؤٹ[7]:

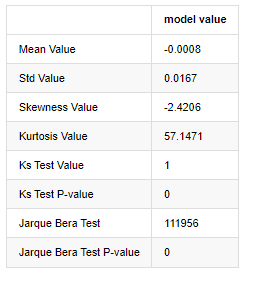
کولموگوروف - سمیرنوف اور جارک - بیرا ٹیسٹ کے اعدادوشمار بالترتیب استعمال کیے جاتے ہیں۔ اصل مفروضہ نمایاں فرق اور معمول کی تقسیم کی خصوصیت رکھتا ہے۔ اگر پی ویلیو 0.05٪ اعتماد کی سطح کی اہم قیمت سے کم ہے تو ، اصل مفروضہ مسترد کردیا جاتا ہے۔

یہ دیکھا جاسکتا ہے کہ کورٹوسس کی قیمت 3 سے زیادہ ہے ، جس سے موٹی چربی کی دم کی خصوصیات ظاہر ہوتی ہیں۔ کے ایس اور جے بی کی پی ویلیوز اعتماد کے وقفے سے کم ہیں۔ معمول کی تقسیم کا مفروضہ مسترد کردیا گیا ہے ، جس سے یہ ثابت ہوتا ہے کہ بی ٹی سی کی واپسی کی شرح میں معمول کی تقسیم کی خصوصیات نہیں ہیں ، اور تجرباتی مطالعہ میں موٹی چربی کی دم کی خصوصیات ہیں۔

1-4۔ حقیقت پسندانہ اور مشاہدہ شدہ اتار چڑھاؤ کا موازنہ

ہم مشاہدات کے لئے square_log_ return (logarithmic yield squared) اور realized_variance (realized variance) کو یکجا کرتے ہیں۔

[11] میں:

fig, ax = plt.subplots(figsize=(18, 6))
start = '2020-03-08 00:00:00+08:00'
end = '2020-03-20 00:00:00+08:00'

np.abs(kline_all['squared_log_return']).loc[start:end].plot(ax=ax,label='squared log return')
kline_all['realized_variance_1_hour'].loc[start:end].plot(ax=ax,label='realized variance')
plt.legend(loc='best')

آؤٹ [11]:

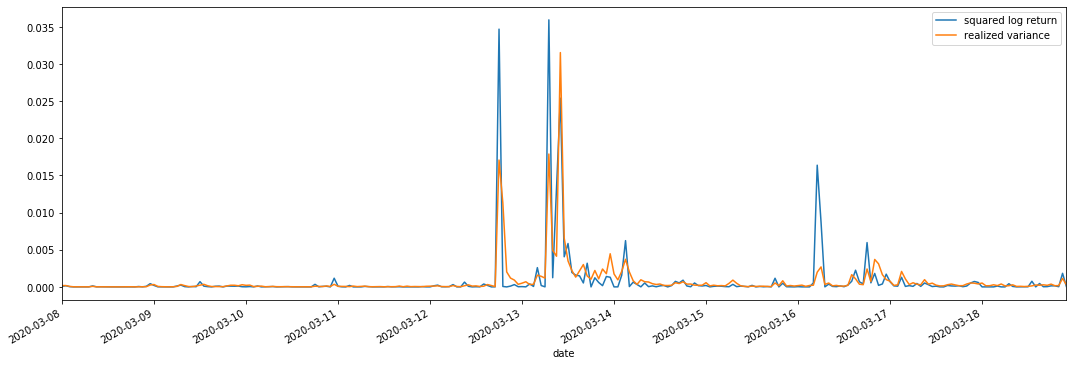
یہ دیکھا جاسکتا ہے کہ جب حقیقت پسندانہ تغیر کی حد بڑی ہوتی ہے تو ، واپسی کی شرح کی حد کی اتار چڑھاؤ بھی بڑی ہوتی ہے ، اور حقیقت پسندانہ واپسی کی شرح ہموار ہوتی ہے۔ ان دونوں میں واضح مجموعی اثرات کا مشاہدہ کرنا آسان ہے۔

خالص نظریاتی نقطہ نظر سے ، آر وی حقیقی اتار چڑھاؤ کے قریب ہے ، جبکہ قلیل مدتی اتار چڑھاؤ کو ہموار کیا جاتا ہے کیونکہ انٹرا ڈے اتار چڑھاؤ راتوں رات کے اعداد و شمار سے تعلق رکھتا ہے ، لہذا مشاہداتی نقطہ نظر سے ، انٹرا ڈے اتار چڑھاؤ اتار چڑھاؤ اسٹاک مارکیٹ میں اتار چڑھاؤ کی کم تعدد کے لئے زیادہ موزوں ہے۔ اعلی تعدد ٹریڈنگ اور بی ٹی سی کی 7 * 24 گھنٹے کی مارکیٹ کی خصوصیات اس کو بینچ مارک اتار چڑھاؤ کا تعین کرنے کے لئے آر وی کا استعمال کرنے کے لئے زیادہ موزوں بناتی ہیں۔

2. وقت کی سیریز کی ہموارگی

اگر یہ ایک غیر مستحکم سیریز ہے تو ، اسے تقریبا ایک مستحکم سیریز میں ایڈجسٹ کرنے کی ضرورت ہے۔ عام طریقہ فرق پروسیسنگ کرنا ہے۔ نظریاتی طور پر ، بہت بار فرق کے بعد ، غیر مستحکم سیریز کو مستحکم سیریز کے قریب کیا جاسکتا ہے۔ اگر نمونہ سیریز کی کوویریئنسی مستحکم ہے تو ، اس کے مشاہدات کی توقع ، تغیر اور کوویریئنسی وقت کے ساتھ تبدیل نہیں ہوگی ، اس سے یہ ظاہر ہوتا ہے کہ نمونہ سیریز شماریاتی تجزیہ میں نتیجہ اخذ کرنے کے لئے زیادہ آسان ہے۔

یونٹ روٹ ٹیسٹ ، یعنی اے ڈی ایف ٹیسٹ ، یہاں استعمال کیا جاتا ہے۔ اے ڈی ایف ٹیسٹ اہمیت کا مشاہدہ کرنے کے لئے ٹی ٹیسٹ کا استعمال کرتا ہے۔ اصولی طور پر ، اگر سلسلہ واضح رجحان نہیں دکھاتا ہے تو ، صرف مستقل آئٹمز کو برقرار رکھا جاتا ہے۔ اگر سلسلہ میں رجحان ہے تو ، رجعت مساوات میں مستقل آئٹمز اور وقت کے رجحان آئٹمز دونوں شامل ہونے چاہئیں۔ اس کے علاوہ ، اے آئی سی اور بی آئی سی کے معیار کو انفارمیشن معیار کی بنیاد پر تشخیص کے لئے استعمال کیا جاسکتا ہے۔ اگر فارمولہ کی ضرورت ہے تو ، یہ مندرجہ ذیل ہے: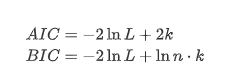

[8] میں:

stable_test = kline_all['log_return']
adftest = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='AIC')
adftest2 = sm.tsa.stattools.adfuller(np.array(stable_test), autolag='BIC')
output=pd.DataFrame(index=['ADF Statistic Test Value', "ADF P-value", "Lags", "Number of Observations",
                           "Critical Value(1%)","Critical Value(5%)","Critical Value(10%)"],
                    columns=['AIC','BIC'])
output['AIC']['ADF Statistic Test Value'] = adftest[0]
output['AIC']['ADF P-value'] = adftest[1]
output['AIC']['Lags'] = adftest[2]
output['AIC']['Number of Observations'] = adftest[3]
output['AIC']['Critical Value(1%)'] = adftest[4]['1%']
output['AIC']['Critical Value(5%)'] = adftest[4]['5%']
output['AIC']['Critical Value(10%)'] = adftest[4]['10%']
output['BIC']['ADF Statistic Test Value'] = adftest2[0]
output['BIC']['ADF P-value'] = adftest2[1]
output['BIC']['Lags'] = adftest2[2]
output['BIC']['Number of Observations'] = adftest2[3]
output['BIC']['Critical Value(1%)'] = adftest2[4]['1%']
output['BIC']['Critical Value(5%)'] = adftest2[4]['5%']
output['BIC']['Critical Value(10%)'] = adftest2[4]['10%']
output

باہر[8]: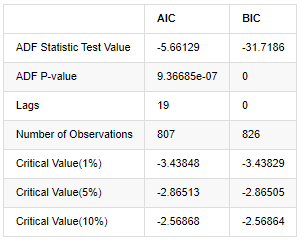

اصل مفروضہ یہ ہے کہ سیریز میں کوئی یونٹ روٹ نہیں ہے ، یعنی متبادل مفروضہ یہ ہے کہ سیریز مستحکم ہے۔ ٹیسٹ پی ویلیو 0.05٪ اعتماد کی سطح کے کٹ آف ویلیو سے کہیں کم ہے ، اصل مفروضے کو مسترد کریں ، لہذا لاگ ریٹ آف رٹرن ایک مستحکم سیریز ہے ، شماریاتی ٹائم سیریز ماڈل کا استعمال کرتے ہوئے ماڈل بنایا جاسکتا ہے۔

ماڈل کی شناخت اور آرڈر کا تعین

درمیانی قدر کے مساوات کو قائم کرنے کے لئے ، یہ یقینی بنانے کے لئے ترتیب پر آٹو کنکشن ٹیسٹ کرنا ضروری ہے کہ غلطی کی اصطلاح میں آٹو کنکشن نہیں ہے۔ پہلے ، آٹو کنکشن ACF اور جزوی کنکشن PACF کو مندرجہ ذیل طریقے سے پلاٹ کرنے کی کوشش کریں:

[19] میں:

tsplot(kline_all['log_return'], kline_all['log_return'], title='Log Return', lags=100)

باہر [1]:

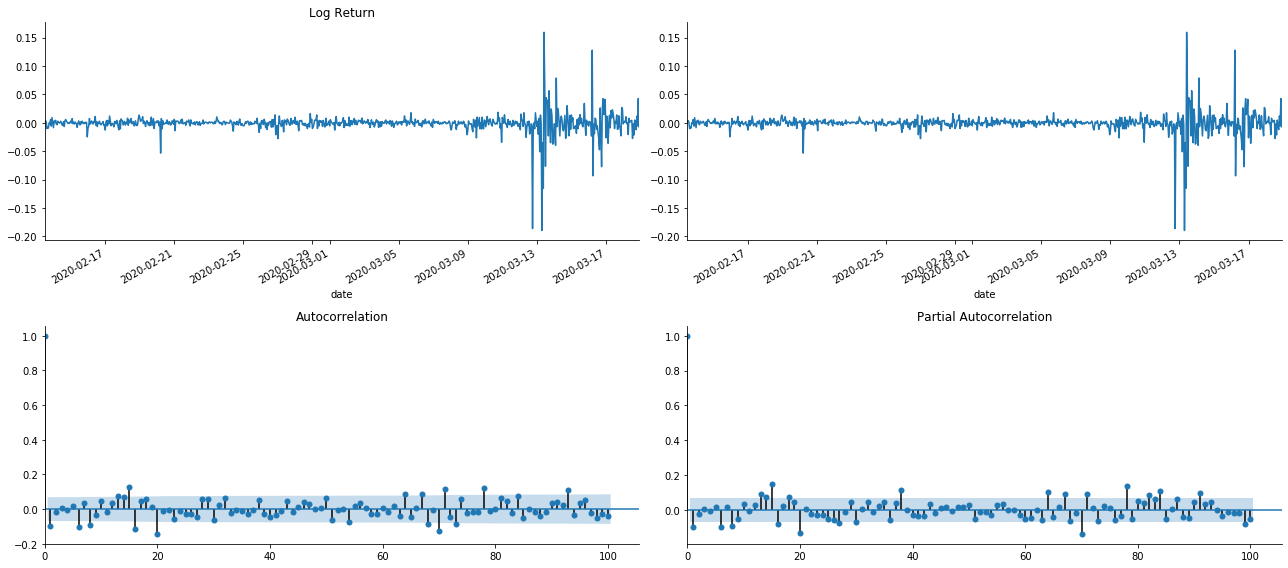
یہ دیکھا جاسکتا ہے کہ ٹرنکشن کا اثر کامل ہے۔ اس لمحے ، اس تصویر نے مجھے ایک الہام دیا۔ کیا مارکیٹ واقعی ناقابل اعتبار ہے؟ اس کی تصدیق کے ل we ، ہم واپسی سیریز پر آٹو کنکشن تجزیہ کریں گے اور ماڈل کے لیگ آرڈر کا تعین کریں گے۔

عام طور پر استعمال ہونے والا ارتباط گتانک اس کے اور خود کے مابین تعلق کی پیمائش کرنا ہے ، یعنی ماضی میں کسی خاص وقت میں r ((t) اور r (t-l) کے مابین تعلق: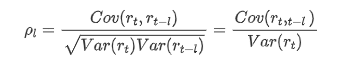

اس کے بعد ہم ایک مقداری ٹیسٹ کرتے ہیں۔ اصل مفروضہ یہ ہے کہ تمام آٹوکوریلیشن گتانک 0 ہیں ، یعنی سیریز میں کوئی آٹوکوریلیشن نہیں ہے۔ ٹیسٹ کے اعدادوشمار کا فارمولا مندرجہ ذیل لکھا گیا ہے: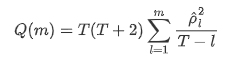

تجزیہ کے لیے دس آٹو کورلیشن کوفیسیئنٹس لیے گئے، مندرجہ ذیل:

[9] میں:

acf,q,p = sm.tsa.acf(kline_all['log_return'], nlags=15,unbiased=True,qstat = True, fft=False)  # Test 10 autocorrelation coefficients
output = pd.DataFrame(np.c_[range(1,16), acf[1:], q, p], columns=['lag', 'ACF', 'Q', 'P-value'])
output = output.set_index('lag')
output

آؤٹ [9]: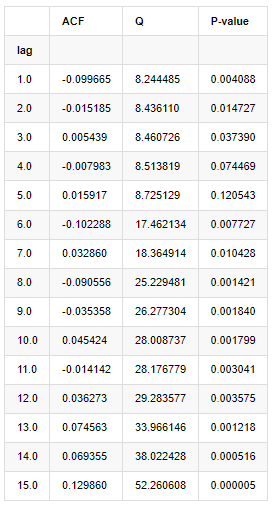

ٹیسٹ کے اعدادوشمار Q اور P-value کے مطابق ہم دیکھ سکتے ہیں کہ آٹو کوریلیشن فنکشن ACF آرڈر 0 کے بعد آہستہ آہستہ 0 بن جاتا ہے۔ Q ٹیسٹ کے اعدادوشمار کے P- اقدار اصل مفروضے کو مسترد کرنے کے لئے کافی چھوٹے ہیں ، لہذا سیریز میں آٹو کوریلیشن ہے۔

آر ایم اے ماڈلنگ

اے آر اور ایم اے ماڈل کافی آسان ہیں۔ اس کو آسان طریقے سے بیان کرنے کے لئے ، مارک ڈاؤن فارمولے لکھنے کے لئے بہت تھکا ہوا ہے۔ اگر آپ دلچسپی رکھتے ہیں تو ، براہ کرم ان کو خود چیک کریں۔ اے آر (آٹو ریگریشن) ماڈل بنیادی طور پر ٹائم سیریز کو ماڈل کرنے کے لئے استعمال کیا جاتا ہے۔ اگر سیریز نے اے سی ایف ٹیسٹ پاس کیا ہے ، یعنی 1 کے وقفے کے ساتھ آٹو کنکشن گتانک اہم ہے ، یعنی وقت کے اعداد و شمار وقت t کی پیش گوئی کے لئے مفید ثابت ہوسکتے ہیں۔

ایم اے (موونگ اوسط) ماڈل موجودہ پیشن گوئی کی قیمت کو لکیری طور پر ظاہر کرنے کے لئے ماضی کی q ادوار کی بے ترتیب مداخلت یا غلطی کی پیش گوئی کا استعمال کرتا ہے۔

اعداد و شمار کی متحرک ساخت کو مکمل طور پر بیان کرنے کے لئے ، اے آر یا ایم اے ماڈلز کے آرڈر کو بڑھانا ضروری ہے ، لیکن ایسے پیرامیٹرز حساب کتاب کو زیادہ پیچیدہ بنادیں گے۔ لہذا ، اس عمل کو آسان بنانے کے لئے ، ایک آٹو ریگریسیو چلتی اوسط (اے آر ایم اے) ماڈل تجویز کیا گیا ہے۔

چونکہ قیمتوں کی وقت کی سیریز عام طور پر غیر مستحکم ہوتی ہے ، اور اسٹیشنری پر فرق کے طریقہ کار کے اصلاح کے اثر پر پہلے ہی تبادلہ خیال کیا گیا ہے ، لہذا اے آر آئی ایم اے (پی ، ڈی ، کیو) (مجموعہ آٹورریگریسیو چلتی اوسط) ماڈل موجودہ ماڈلز کو سیریز میں لاگو کرنے کی بنیاد پر ڈی آرڈر فرق پروسیسنگ کا اضافہ کرتا ہے۔ تاہم ، چونکہ ہم نے لوگرتھم استعمال کیے ہیں ، لہذا ہم براہ راست اے آر ایم اے (پی ، کیو) استعمال کرسکتے ہیں۔

ایک لفظ میں ، اے آر آئی ایم اے ماڈل اور اے آر ایم اے ماڈل بنانے کے عمل میں صرف ایک ہی فرق یہ ہے کہ اگر مستحکم نتائج کا تجزیہ کرنے کے بعد مستحکم نتائج حاصل کیے جاتے ہیں تو ، ماڈل براہ راست سیریز میں مربع فرق کرے گا اور پھر مستحکم ٹیسٹ انجام دے گا ، اور پھر سیریز مستحکم ہونے تک آرڈر پی اور کیو کا تعین کرے گا۔ ماڈل بنانے اور اس کا اندازہ کرنے کے بعد ، بعد میں پیش گوئی کی جائے گی ، جس سے فرق کرنے کے لئے واپس جانے کا مرحلہ ختم ہوجائے گا۔ تاہم ، قیمت کا دوسرا آرڈر کا فرق بے معنی ہے ، لہذا اے آر ایم اے بہترین انتخاب ہے۔

آرڈر کا انتخاب

اگلا، ہم براہ راست معلومات کے معیار کی طرف سے ترتیب منتخب کر سکتے ہیں، یہاں ہم AIC اور BIC کے حرارتی ڈایاگرام کے ساتھ کوشش کرتے ہیں.

[10] میں:

def select_best_params():
    ps = range(0, 4)
    ds= range(1, 2)
    qs = range(0, 4)
    parameters = product(ps, ds, qs)
    parameters_list = list(parameters)

    p_min = 0
    d_min = 0
    q_min = 0
    p_max = 3
    d_max = 3
    q_max = 3

    results_aic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
                               columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
    
    best_params = []
    aic_results = []
    bic_results = []
    hqic_results = []
    best_aic = float("inf")
    best_bic = float("inf")
    best_hqic = float("inf")
    warnings.filterwarnings('ignore')
    for param in parameters_list:
        try:
            model = sm.tsa.SARIMAX(kline_all['log_price'], order=(param[0], param[1], param[2])).fit(disp=-1)
            results_aic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.aic
            results_bic.loc['AR{}'.format(param[0]), 'MA{}'.format(param[2])] = model.bic
        except ValueError:
            continue    
           
        aic_results.append([param, model.aic])
        bic_results.append([param, model.bic])
        hqic_results.append([param, model.hqic])
    
    results_aic = results_aic[results_aic.columns].astype(float)
    results_bic = results_bic[results_bic.columns].astype(float)
    
    # Draw thermodynamic diagrams of AIC and BIC to find the best
    fig = plt.figure(figsize=(18, 9))
    layout = (2, 2)
    aic_ax = plt.subplot2grid(layout, (0, 0))
    bic_ax = plt.subplot2grid(layout, (0, 1))

    aic_ax = sns.heatmap(results_aic,mask=results_aic.isnull(),ax=aic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    aic_ax.set_title('AIC');
    bic_ax = sns.heatmap(results_bic,mask=results_bic.isnull(),ax=bic_ax,cmap='OrRd',annot=True,fmt='.2f',);
    bic_ax.set_title('BIC');
    
    aic_df = pd.DataFrame(aic_results)
    aic_df.columns = ['params', 'aic']   
    best_params.append(aic_df.params[aic_df.aic.idxmin()])
    print('AIC best param: {}'.format(aic_df.params[aic_df.aic.idxmin()]))
    
    bic_df = pd.DataFrame(bic_results)
    bic_df.columns = ['params', 'bic']
    best_params.append(bic_df.params[bic_df.bic.idxmin()])
    print('BIC best param: {}'.format(bic_df.params[bic_df.bic.idxmin()]))
    
    hqic_df = pd.DataFrame(hqic_results)
    hqic_df.columns = ['params', 'hqic']
    best_params.append(hqic_df.params[hqic_df.hqic.idxmin()])
    print('HQIC best param: {}'.format(hqic_df.params[hqic_df.hqic.idxmin()]))

    for best_param in best_params:
        if best_params.count(best_param)>=2:
            print('Best Param Selected: {}'.format(best_param))
            return best_param 

best_param = select_best_params()

باہر[10]: AIC بہترین پیرامیٹر: (0, 1, 1) بی آئی سی بہترین پیرام: (0, 1, 1) HQIC بہترین پیرامیٹر: (0, 1, 1) بہترین پیرام منتخب: (0, 1, 1)

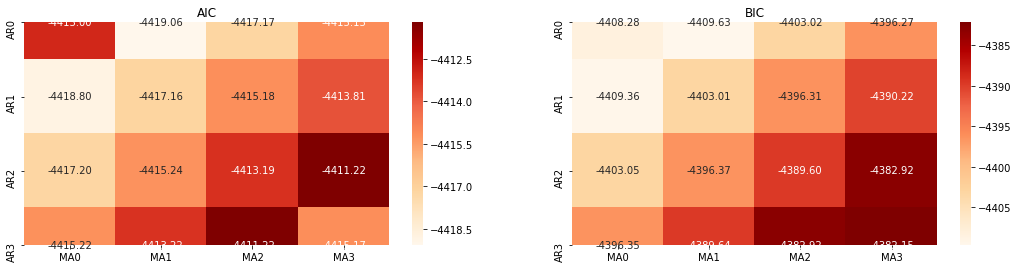
یہ واضح ہے کہ لوگرتھمک قیمت کے لئے بہترین پہلے آرڈر کے پیرامیٹر مجموعہ (0,1,1) ہے ، جو آسان اور سیدھا ہے۔ لاگ_ریٹرن (لوگرتھمک شرح واپسی) ایک ہی آپریشن انجام دیتا ہے۔ اے آئی سی کی زیادہ سے زیادہ قیمت (4,3) ہے ، اور بی آئی سی کی زیادہ سے زیادہ قیمت (0,1) ہے۔ لہذا لاگ_ریٹرن (لوگرتھمک شرح واپسی) کے لئے پیرامیٹرز کا زیادہ سے زیادہ مجموعہ (0,1) ہے۔

آر ایم اے ماڈلنگ اور مماثلت

سہ ماہی گتانکوں کی ضرورت نہیں ہے، لیکن SARIMAX صفات میں زیادہ امیر ہے، لہذا ماڈلنگ کے لئے اس ماڈل کا انتخاب کرنے کا فیصلہ کیا گیا تھا اور اتفاق سے مندرجہ ذیل طور پر ایک وضاحتی تجزیہ تیار کیا گیا تھا:

[11] میں:

params = (0, 0, 1)
training_model = smt.SARIMAX(endog=kline_all['log_return'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
model_results = training_model.fit(disp=False)
model_results.summary()

آؤٹ [11]: اسٹیٹس اسپیس ماڈل کے نتائج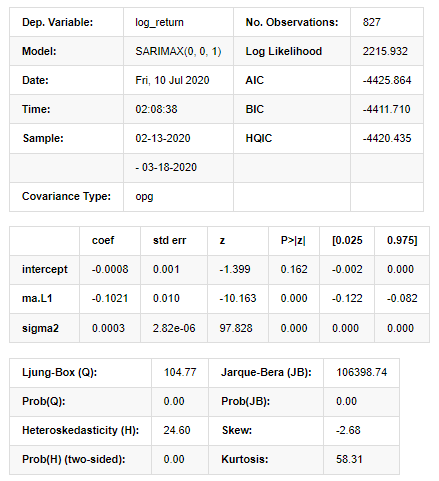

انتباہ: [1] گریڈیئنٹس کے بیرونی مصنوعہ (پیچیدہ مرحلہ) کا استعمال کرتے ہوئے حساب لگایا گیا کوویریئنس میٹرکس۔ [27] میں:

model_results.plot_diagnostics(figsize=(18, 10));

باہر [1]:

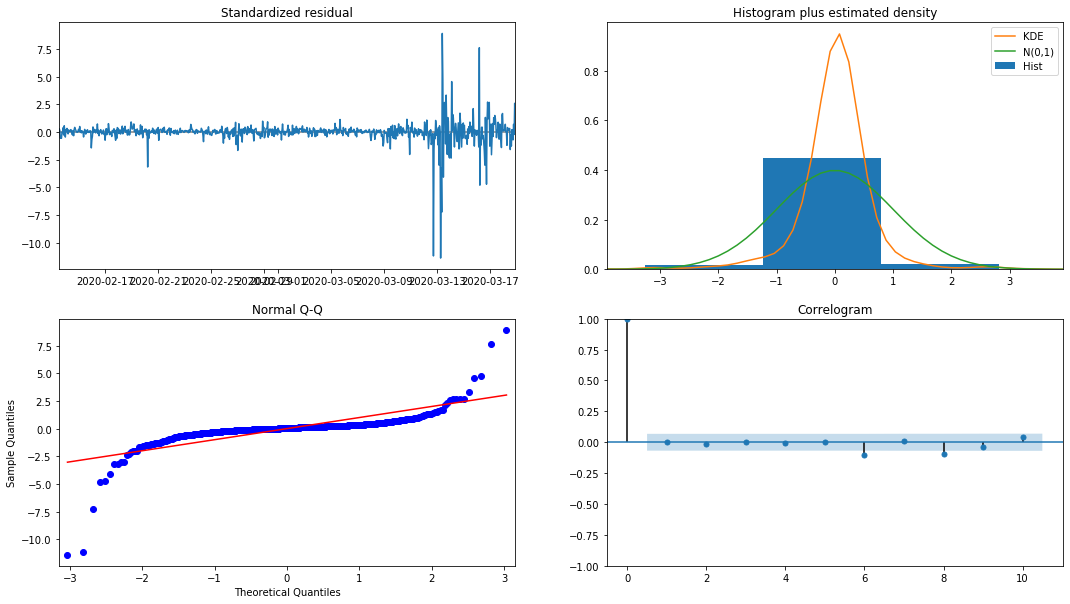
ہسٹوگرام میں احتمال کثافت KDE معمول کی تقسیم N (0,1) سے دور ہے ، اس بات کی نشاندہی کرتی ہے کہ بقایا معمول کی تقسیم نہیں ہے۔ QQ کوانٹائل پلاٹ میں ، معیاری معمول کی تقسیم سے نمونے لینے والے نمونوں کے بقایا مکمل طور پر لکیری رجحان کی پیروی نہیں کرتے ہیں ، لہذا یہ ایک بار پھر تصدیق کی گئی ہے کہ بقایا معمول کی تقسیم نہیں ہیں اور وہ وائٹ شور کے قریب ہیں۔

پھر، یہ کہہ کر، کیا ماڈل استعمال کیا جا سکتا ہے اب بھی ٹیسٹ کرنے کی ضرورت ہے.

ماڈل ٹیسٹ

بقایا کا مماثلت اثر مثالی نہیں ہے ، لہذا ہم نے اس پر ڈربن واٹسن ٹیسٹ انجام دیا۔ ٹیسٹ کا اصل مفروضہ یہ ہے کہ ترتیب میں آٹو کنکشن نہیں ہے ، اور متبادل مفروضہ ترتیب مستحکم ہے۔ اس کے علاوہ ، اگر ایل بی ، جے بی اور ایچ ٹیسٹوں کی پی ویلیوز 0.05٪ اعتماد کی سطح کی اہم قیمت سے کم ہیں تو ، اصل مفروضہ مسترد ہوجائے گا۔

میں [12]:

het_method='breakvar'
norm_method='jarquebera'
sercor_method='ljungbox'

(het_stat, het_p) = model_results.test_heteroskedasticity(het_method)[0]
norm_stat, norm_p, skew, kurtosis = model_results.test_normality(norm_method)[0]

sercor_stat, sercor_p = model_results.test_serial_correlation(method=sercor_method)[0]
sercor_stat = sercor_stat[-1] # The last value of the maximum period
sercor_p = sercor_p[-1]

dw = sm.stats.stattools.durbin_watson(model_results.filter_results.standardized_forecasts_error[0, model_results.loglikelihood_burn:])

arroots_outside_unit_circle = np.all(np.abs(model_results.arroots) > 1)
maroots_outside_unit_circle = np.all(np.abs(model_results.maroots) > 1)

print('Test heteroskedasticity of residuals ({}): stat={:.3f}, p={:.3f}'.format(het_method, het_stat, het_p));
print('\nTest normality of residuals ({}): stat={:.3f}, p={:.3f}'.format(norm_method, norm_stat, norm_p));
print('\nTest serial correlation of residuals ({}): stat={:.3f}, p={:.3f}'.format(sercor_method, sercor_stat, sercor_p));
print('\nDurbin-Watson test on residuals: d={:.2f}\n\t(NB: 2 means no serial correlation, 0=pos, 4=neg)'.format(dw))
print('\nTest for all AR roots outside unit circle (>1): {}'.format(arroots_outside_unit_circle))
print('\nTest for all MA roots outside unit circle (>1): {}'.format(maroots_outside_unit_circle))

root_test=pd.DataFrame(index=['Durbin-Watson test on residuals','Test for all AR roots outside unit circle (>1)','Test for all MA roots outside unit circle (>1)'],columns=['c'])
root_test['c']['Durbin-Watson test on residuals']=dw
root_test['c']['Test for all AR roots outside unit circle (>1)']=arroots_outside_unit_circle
root_test['c']['Test for all MA roots outside unit circle (>1)']=maroots_outside_unit_circle
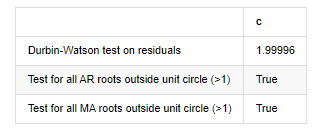
root_test

آؤٹ [1]: باقیات کی ٹیسٹ heteroskedasticity (breakvar): stat=24.598، p=0.000

باقیات (جارکیبیرا) کے ٹیسٹ کی نارملٹی: stat=106398.739، p=0.000

باقیات کا ٹیسٹ سیریل ارتباط (جنگ باکس): stat=104.767، p=0.000

باقیات پر ڈربن واٹسن ٹیسٹ: d=2.00 (نوٹ: 2 کا مطلب ہے کوئی سیریل ارتباط نہیں، 0=pos، 4=neg)

یونٹ سرکل (> 1) کے باہر تمام AR جڑوں کے لئے ٹیسٹ: درست

یونٹ سرکل کے باہر تمام MA جڑوں کے لئے ٹیسٹ (> 1): درست

[13] میں:

kline_all['log_price_dif1'] = kline_all['log_price'].diff(1)
kline_all = kline_all[1:]
kline_train = kline_all

training_label = 'log_return'
training_ts = pd.DataFrame(kline_train[training_label], dtype=np.float)

delta = model_results.fittedvalues - training_ts[training_label]
adjR = 1 - delta.var()/training_ts[training_label].var()
adjR_test=pd.DataFrame(index=['adjR2'],columns=['Value'])
adjR_test['Value']['adjR2']=adjR**2
adjR_test

آؤٹ [1]:

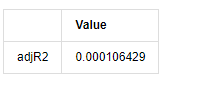
اگر ڈربن واٹسن ٹیسٹ کا اعدادوشمار 2 کے برابر ہے تو ، اس بات کی تصدیق ہوتی ہے کہ سیریز کا کوئی تعلق نہیں ہے ، اور اس کی شماریاتی قیمت (0,4) کے درمیان تقسیم کی جاتی ہے۔ 0 کے قریب ہونے کا مطلب ہے کہ مثبت تعلق زیادہ ہے ، جبکہ 4 کے قریب ہونے کا مطلب ہے کہ منفی تعلق زیادہ ہے۔ یہاں یہ تقریبا برابر ہے۔ دوسرے ٹیسٹوں کی P قیمت کافی کم ہے ، یونٹ کی خصوصیت کی جڑ یونٹ دائرے سے باہر ہے ، اور ترمیم شدہ ایڈج آر 2 کی قدر جتنی زیادہ ہوگی ، اتنا ہی بہتر ہوگا۔ پیمائش کا مجموعی نتیجہ اطمینان بخش نہیں لگتا ہے۔

[14] میں:

model_results.params

باہر [1]: روکنا -0.000817 ma.L1 -0.102102 سیگما2 0.000275 dtype: float64

خلاصہ یہ ہے کہ ، آرڈر سیٹنگ پیرامیٹر بنیادی طور پر وقت کی سیریز کی ماڈلنگ اور اس کے بعد اتار چڑھاؤ کی ماڈلنگ کی ضروریات کو پورا کرسکتا ہے ، لیکن مماثلت کا اثر ایسا ہی ہے۔ ماڈل کا اظہار مندرجہ ذیل ہے: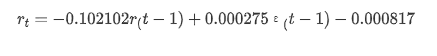

4-4. ماڈل کی پیش گوئی

اس کے بعد ، تربیت یافتہ ماڈل کو آگے بڑھا دیا جاتا ہے۔ اعدادوشمار ماڈل مماثلت اور پیش گوئی کے لئے جامد اور متحرک اختیارات فراہم کرتے ہیں۔ فرق اس میں ہے کہ آیا مشاہدے کی قیمت پیش گوئی کے اگلے مرحلے میں استعمال کی جاتی ہے ، یا پچھلے مرحلے میں پیدا ہونے والی پیش گوئی کی قیمت کو تکرار کے ساتھ استعمال کیا جاتا ہے۔ لاگ_ریٹرن (ریٹرن کی لوگرتھمک شرح) کے پیش گوئی کے اثرات مندرجہ ذیل ہیں:

[37] میں:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

باہر [1]:

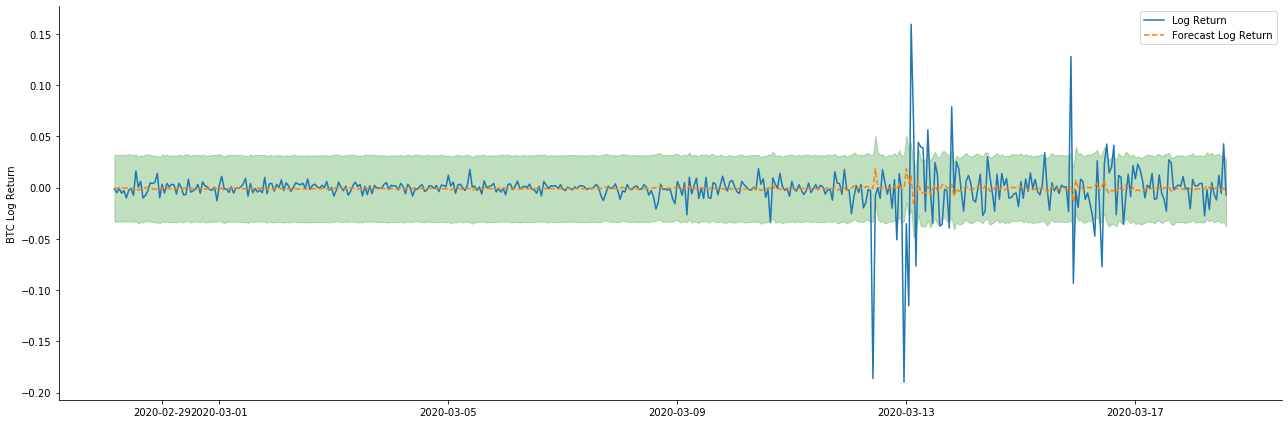
یہ دیکھا جا سکتا ہے کہ نمونہ پر جامد موڈ کا فٹ ہونے کا اثر بہترین ہے، نمونہ کے اعداد و شمار تقریبا 95٪ اعتماد کے وقفے سے احاطہ کر سکتے ہیں، اور متحرک موڈ تھوڑا سا کنٹرول سے باہر ہے.

تو آئیے متحرک موڈ میں ڈیٹا مماثلت اثر کو دیکھتے ہیں:

[38] میں:

start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date 

pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()

fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)

plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()

باہر [1]:

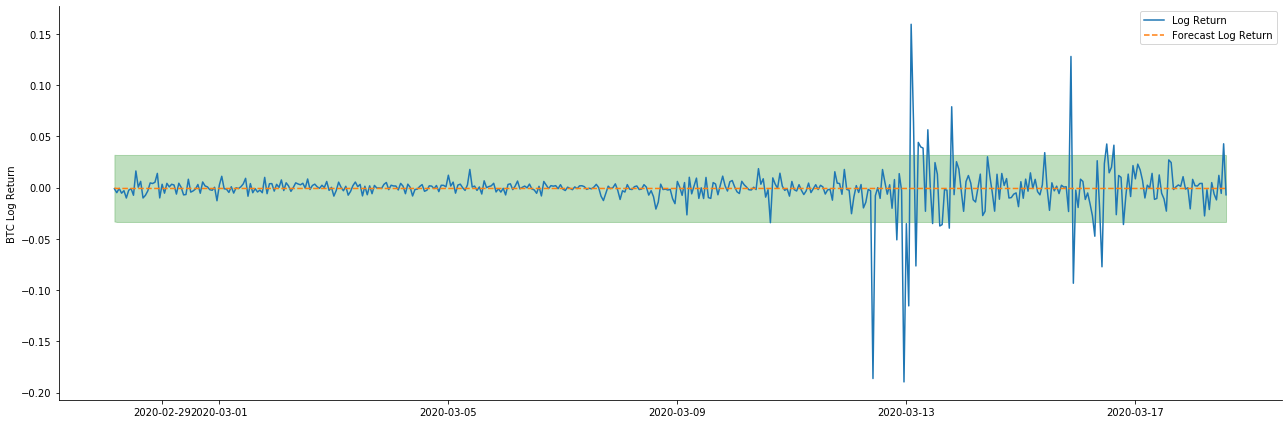
یہ دیکھا جاسکتا ہے کہ نمونہ پر دونوں ماڈلز کا فٹ ہونے کا اثر بہترین ہے ، اور اوسط قیمت تقریبا 95٪ اعتماد کے وقفے سے احاطہ کی جاسکتی ہے ، لیکن جامد ماڈل ظاہر ہے کہ زیادہ موزوں ہے۔ اگلا ، آئیے نمونہ سے باہر 50 اقدامات ، یعنی پہلے 50 گھنٹوں کے پیش گوئی کے اثر کو دیکھیں:

[41] میں:

# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False

predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]

predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]

fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')

predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)

predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

باہر[41]:

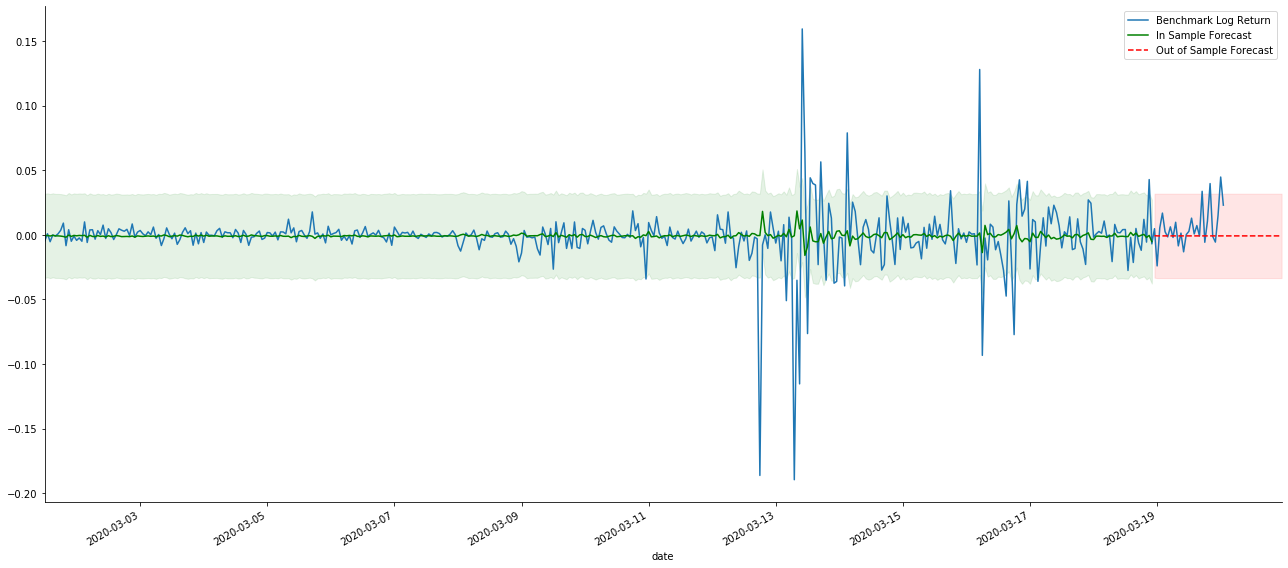
چونکہ نمونہ میں اعداد و شمار کا مماثلت ایک رولنگ فارورڈ پیشن گوئی ہے ، جب نمونہ میں موجود معلومات کی مقدار کافی ہوتی ہے تو ، جامد ماڈل زیادہ مماثلت کا شکار ہوتا ہے ، جبکہ متحرک ماڈل میں قابل اعتماد منحصر متغیرات کا فقدان ہوتا ہے ، اور تکرار کے بعد اثر بدتر ہوتا جاتا ہے۔ جب نمونہ سے باہر کے اعداد و شمار کی پیش گوئی کرتے ہیں تو ، ماڈل نمونہ کے اندر متحرک ماڈل کے برابر ہوتا ہے ، لہذا طویل مدتی پیشن گوئی کی غلطی کی درستگی کم ہونے کا پابند ہے۔

اگر ہم واپسی کی شرح کی پیشن گوئی کو لاگ_پریس (لوگرتھمک قیمت) میں تبدیل کرتے ہیں تو ، میچ ذیل کے اعداد و شمار میں دکھایا گیا ہے:

[42] میں:

params = (0, 1, 1)
mod = smt.SARIMAX(endog=kline_all['log_price'], trend='c', order=params, seasonal_order=(0, 0, 0, 0))
res = mod.fit(disp=False)

start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-15 23:00:00+08:00'

predicts_ARIMA_normal = res.get_prediction(start=start_date, dynamic=False, full_results=False)
predicts_ARIMA_dynamic = res.get_prediction(start=start_date, dynamic=True, full_results=False)

fig, ax = plt.subplots(figsize=(18,6))
kline_test.loc[start_date:end_date, 'log_price'].plot(ax=ax, label='Log Price')

predicts_ARIMA_normal.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='r--', label='Normal Prediction')
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:end_date]
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='r', alpha=0.1)

predicts_ARIMA_dynamic.predicted_mean.loc[start_date:end_date].plot(ax=ax, style='g', label='Dynamic Prediction')
ci_dynamic = predicts_ARIMA_dynamic.conf_int().loc[start_date:end_date]
ax.fill_between(ci_dynamic.index, ci_dynamic.iloc[:,0], ci_dynamic.iloc[:,1], color='g', alpha=0.1)

plt.tight_layout()
plt.legend(loc='best')
sns.despine()

باہر[42]:

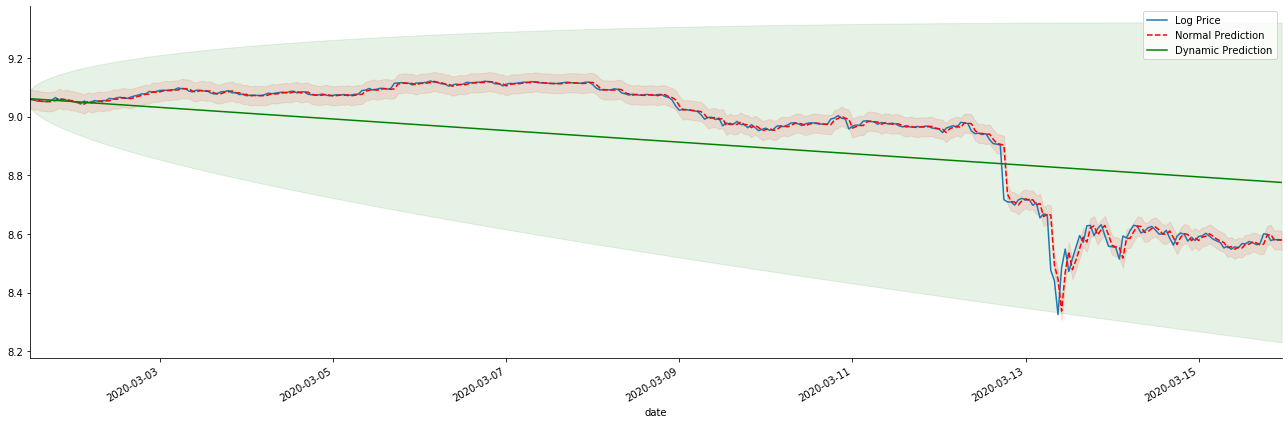
یہ دیکھنا آسان ہے کہ جامد ماڈل کے مماثل فوائد اور طویل مدتی پیش گوئی میں متحرک ماڈل اور جامد ماڈل کے مابین انتہائی فرق ہے۔ سرخ نقطے والی لائن اور گلابی رینج... آپ یہ نہیں کہہ سکتے کہ اس ماڈل کی پیش گوئی غلط ہے۔ آخر میں ، یہ حرکت پذیر اوسط کے رجحان کو مکمل طور پر ڈھکتا ہے ، لیکن... کیا اس کا کوئی مطلب ہے؟

حقیقت میں ، اے آر ایم اے ماڈل خود غلط نہیں ہے ، کیونکہ مسئلہ خود ماڈل نہیں ہے ، بلکہ چیزوں کی معروضی منطق خود ہے۔ ٹائم سیریز ماڈل صرف پچھلے اور بعد کے مشاہدات کے مابین ارتباط کی بنیاد پر قائم کیا جاسکتا ہے۔ لہذا ، سفید شور کی سیریز کا ماڈل بنانا ناممکن ہے۔ لہذا ، پچھلے تمام کام اس جرات مندانہ مفروضے پر مبنی ہیں کہ بی ٹی سی کی واپسی کی شرح سیریز آزاد اور یکساں طور پر تقسیم نہیں ہوسکتی ہے۔

عام طور پر ، واپسی کی شرح سیریز مارٹنگیل فرق سیریز ہیں ، جس کا مطلب ہے کہ واپسی کی شرح غیر متوقع ہے ، اور اسی مارکیٹ کی کمزور کارکردگی کا مفروضہ برقرار ہے۔ ہم نے فرض کیا ہے کہ انفرادی نمونے میں واپسی کی شرح میں آٹو کنکشن کی ایک خاص ڈگری ہے ، اور اسی تقسیم کا مفروضہ یہ بھی ہے کہ مماثلت کا ماڈل ٹریننگ سیٹ پر لاگو کیا جائے ، تاکہ ایک سادہ اے آر ایم اے ماڈل کو مماثل کیا جاسکے ، جس کا پیش گوئی کا اثر کمزور ہونا ضروری ہے۔

تاہم ، مماثل بقایا ترتیب بھی ایک مارٹنگیل فرق ترتیب ہے۔ مارٹنگیل فرق ترتیب آزاد اور یکساں طور پر تقسیم نہیں ہوسکتی ہے ، لیکن مشروط تغیر ماضی کی قیمت پر منحصر ہوسکتا ہے ، لہذا پہلے آرڈر کا آٹو کنکشن ختم ہوگیا ہے ، لیکن پھر بھی اعلی آرڈر کا آٹو کنکشن موجود ہے ، جو اتار چڑھاؤ کو ماڈل کرنے اور مشاہدہ کرنے کی ایک اہم شرط بھی ہے۔

اگر اس طرح کا منطق درست ہے تو ، پھر مختلف اتار چڑھاؤ کے ماڈل بنانے کی شرط بھی درست ہے۔ لہذا واپسی کی شرح کی سیریز کے ل if ، اگر کمزور موثر مارکیٹ مطمئن ہے تو ، اس وقت اوسط قدر کی پیش گوئی کرنا مشکل ہونا ضروری ہے ، لیکن تغیر قابل پیش گوئی ہے۔ اور مماثل اے آر ایم اے ایک منصفانہ معیار کی ٹائم سیریز بینچ مارک فراہم کرتا ہے ، پھر معیار اتار چڑھاؤ کی پیش گوئی کے معیار کا تعین کرتا ہے۔

آخر میں ، آئیے اس پیش گوئی کے اثر کا جائزہ لیتے ہیں۔ تشخیص کے معیار کے طور پر غلطی کے ساتھ ، نمونے کے اندر اور باہر کے اشارے مندرجہ ذیل ہیں۔

[15] میں:

start = '2020-02-14 00:00:00+08:00'
predicts_ARIMA_normal = model_results.get_prediction(dynamic=False)
predicts_ARIMA_dynamic = model_results.get_prediction(dynamic=True)
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [rmse(predicts_ARIMA_normal.predicted_mean[1:], kline_test[training_label][:826]),
                          rmse(predicts_ARIMA_dynamic.predicted_mean[1:], kline_test[training_label][:826])]
compare_ARCH_X['MAPE'] = [mape(predicts_ARIMA_normal.predicted_mean[:50], kline_test[training_label][:50]),
                          mape(predicts_ARIMA_dynamic.predicted_mean[:50], kline_test[training_label][:50])]
compare_ARCH_X

باہر[15]: جڑ اوسط مربع غلطی (RMSE): 0.0184 جڑ اوسط مربع غلطی (RMSE): 0.0167 اوسط مطلق فیصد غلطی (MAPE): 2.25e+03 اوسط مطلق فیصد غلطی (MAPE): 395

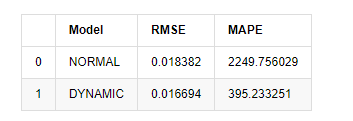
یہ دیکھا جاسکتا ہے کہ متحرک ماڈل متوقع قیمت اور اصل قیمت کے مابین غلطی کے اتفاق کے لحاظ سے متحرک ماڈل سے قدرے بہتر ہے۔ یہ بٹ کوائن کی لوگرتھمک واپسی کی شرح سے اچھی طرح ملتا ہے ، جو بنیادی طور پر توقعات کے مطابق ہے۔ متحرک پیش گوئی میں زیادہ درست متغیر معلومات کی کمی ہے ، اور غلطی کو بھی تکرار کے ذریعہ بڑھا دیا جاتا ہے ، لہذا پیش گوئی کا اثر خراب ہے۔ MAPE 100٪ سے زیادہ ہے ، لہذا دونوں ماڈلز کا اصل مماثلت کا معیار مثالی نہیں ہے۔

[18] میں:

predict_step = 50
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=False)
predicts_ARIMA_dynamic_out = model_results.get_forecast(steps=predict_step, dynamic=True)
testing_ts = kline_test
training_label = 'log_return'

compare_ARCH_X = pd.DataFrame()
compare_ARCH_X['Model'] = ['NORMAL','DYNAMIC']
compare_ARCH_X['RMSE'] = [get_rmse(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_rmse(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X['MAPE'] = [get_mape(predicts_ARIMA_normal_out.predicted_mean, testing_ts[training_label]),
                          get_mape(predicts_ARIMA_dynamic_out.predicted_mean, testing_ts[training_label])]
compare_ARCH_X

باہر [1]:

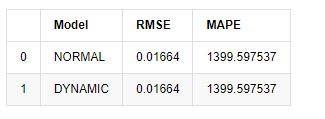
چونکہ نمونہ سے باہر اگلی پیش گوئی پچھلے مرحلے کے نتائج پر منحصر ہے ، لہذا صرف متحرک ماڈل ہی موثر ہے۔ تاہم ، متحرک ماڈل کا طویل مدتی غلطی کا نقص مجموعی ماڈل کی ناکافی پیش گوئی کی صلاحیت کا باعث بنتا ہے ، لہذا اگلے مرحلے کی پیش گوئی زیادہ سے زیادہ کی جاتی ہے۔

خلاصہ یہ کہ ، اے آر ایم اے ماڈل جامد ماڈل بٹ کوائن کی انٹرا نمونہ شرح واپسی سے ملنے کے لئے موزوں ہے۔ شرح واپسی کی قلیل مدتی پیش گوئی اعتماد کے وقفے کو مؤثر طریقے سے ڈھک سکتی ہے ، لیکن طویل مدتی پیش گوئی بہت مشکل ہے ، جو مارکیٹ کی کمزور تاثیر کو پورا کرتی ہے۔ جانچ کے بعد ، نمونہ وقفے کے اندر واپسی کی شرح بعد میں اتار چڑھاؤ کے مشاہدے کے مفروضے کو پورا کرتی ہے۔

5. آرچ اثر

آرچ ماڈل اثر مشروط ہیٹروسکیڈاسٹیٹی ترتیب کا سیریز رابطہ ہے۔ مرکب ٹیسٹ ایلجنگ باکس کا استعمال باقی مربع سیریز کے رابطے کو جانچنے کے لئے کیا جاتا ہے تاکہ یہ معلوم کیا جاسکے کہ آیا آرچ اثر موجود ہے۔ اگر آرچ اثر ٹیسٹ پاس ہوجاتا ہے ، یعنی ، سیریز میں ہیٹروسکیڈاسٹیٹیٹی ہے تو ، گارچ ماڈلنگ کا اگلا مرحلہ مشترکہ طور پر اوسط مساوات اور اتار چڑھاؤ کے مساوات کا اندازہ لگانے کے لئے کیا جاسکتا ہے۔ بصورت دیگر ، ماڈل کو بہتر بنانے اور دوبارہ ایڈجسٹ کرنے کی ضرورت ہے ، جیسے تفریقی پروسیسنگ یا باہمی سیریز۔

ہم یہاں کچھ ڈیٹا سیٹ اور عالمی متغیرات تیار کرتے ہیں:

[33] میں:

count_num = 100000
start_date = '2020-03-01'

df = get_bars('huobi.btc_usdt', '1m', count=count_num, start=start_date)  # Take the minute data
kline_1m = pd.DataFrame(df['close'], dtype=np.float)
kline_1m.index.name = 'date'
kline_1m['log_price'] = np.log(kline_1m['close'])
kline_1m['return'] = kline_1m['close'].pct_change().dropna()
kline_1m['log_return'] = kline_1m['log_price'] - kline_1m['log_price'].shift(1)

kline_1m['squared_log_return'] = np.power(kline_1m['log_return'], 2)

kline_1m['return_100x'] = np.multiply(kline_1m['return'], 100)
kline_1m['log_return_100x'] = np.multiply(kline_1m['log_return'], 100)  # Enlarge 100 times

df = get_bars('huobi.btc_usdt', '1h', count=count_num, start=start_date)  # Take the hour data
kline_test = pd.DataFrame(df['close'], dtype=np.float)
kline_test.index.name = 'date'
kline_test['log_price'] = np.log(kline_test['close'])  # Calculate the daily logarithmic rate of return
kline_test['return'] = kline_test['log_price'].pct_change().dropna()
kline_test['log_return'] = kline_test['log_price'] - kline_test['log_price'].shift(1)  # Calculate the logarithmic rate of return
kline_test['squared_log_return'] = np.power(kline_test['log_return'], 2)  # Exponential square of log daily return rate

kline_test['return_100x'] = np.multiply(kline_test['return'], 100)
kline_test['log_return_100x'] = np.multiply(kline_test['log_return'], 100)  # Enlarge 100 times

kline_test['realized_variance_1_hour'] = kline_1m.loc[:, 'squared_log_return'].resample('h', closed='left', label='left').sum().copy() # Resampling to days 
kline_test['realized_volatility_1_hour'] = np.sqrt(kline_test['realized_variance_1_hour'])  # Volatility of variance derivation

kline_test = kline_test[4:-2500]
kline_test.head(3)

آؤٹ [33]:

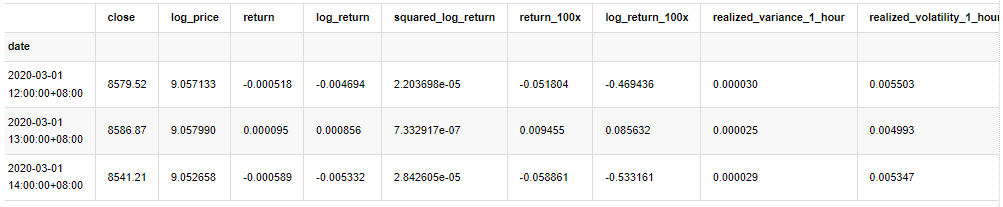
[22] میں:

cc = 3
model_p = 1
predict_lag = 30
label = 'log_return'

training_label = label
training_ts = pd.DataFrame(kline_test[training_label], dtype=np.float)

training_arch_label = label
training_arch = pd.DataFrame(kline_test[training_arch_label], dtype=np.float)

training_garch_label = label
training_garch = pd.DataFrame(kline_test[training_garch_label], dtype=np.float)

training_egarch_label = label
training_egarch = pd.DataFrame(kline_test[training_egarch_label], dtype=np.float)

training_arch.plot(figsize = (18,4))

باہر[22]: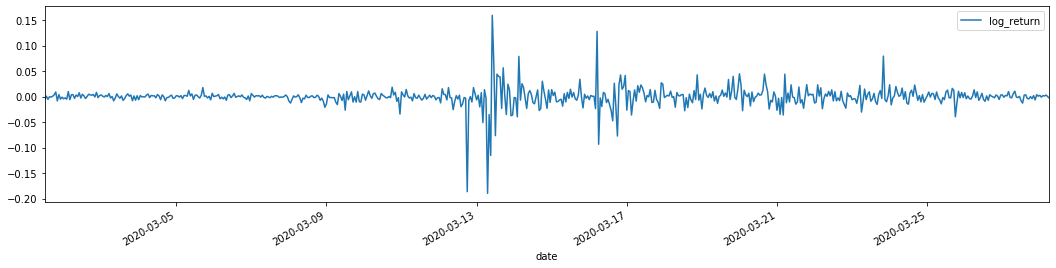

لوگرتھمک واپسی کی شرحیں اوپر دکھائی گئی ہیں۔ اگلا ، ہمیں نمونہ کے آرچ اثر کا تجربہ کرنے کی ضرورت ہے۔ ہم اے آر ایم اے کی بنیاد پر نمونہ کے اندر بقایا سیریز قائم کرتے ہیں۔ کچھ سیریز اور بقایا اور بقایا کی مربع سیریز پہلے حساب کی جاتی ہے۔

[20] میں:

training_arma_model = smt.SARIMAX(endog=training_ts, trend='c', order=(0, 0, 1), seasonal_order=(0, 0, 0, 0))
arma_model_results = training_arma_model.fit(disp=False)
arma_model_results.summary()
training_arma_fitvalue = pd.DataFrame(arma_model_results.fittedvalues,dtype=np.float)
at = pd.merge(training_ts, training_arma_fitvalue, on='date')
at.columns = ['log_return', 'model_fit']
at['res'] = at['log_return'] - at['model_fit']
at['res2'] = np.square(at['res'])
at.head()

باہر[20]:

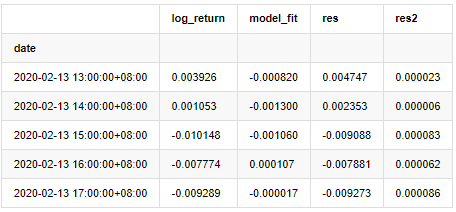
اس کے بعد نمونہ کی بقایا سیریز کو پلاٹ کیا جاتا ہے

[69] میں:

fig, ax = plt.subplots(figsize=(18, 6))
ax1 = fig.add_subplot(2,1,1)
at['res'][1:].plot(ax=ax1,label='resid')
plt.legend(loc='best')

ax2 = fig.add_subplot(2,1,2)
at['res2'][1:].plot(ax=ax2,label='resid2')

plt.legend(loc='best')
plt.tight_layout()
sns.despine()

آؤٹ [1]:

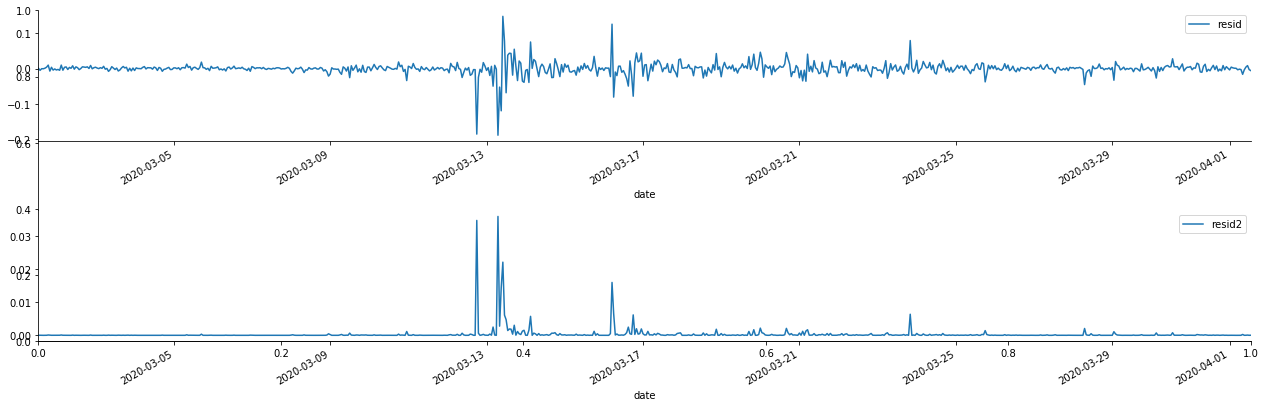
یہ دیکھا جاسکتا ہے کہ بقایا سیریز میں واضح مجموعی خصوصیات ہیں ، اور یہ ابتدائی طور پر فیصلہ کیا جاسکتا ہے کہ سیریز میں آرچ اثر ہے۔ ACF کو مربع باقیات کے آٹو کنکشن کی جانچ کے لئے بھی لیا جاتا ہے ، اور نتائج مندرجہ ذیل ہیں۔

[70] میں:

figure = plt.figure(figsize=(18,4))
ax1 = figure.add_subplot(111)
fig = sm.graphics.tsa.plot_acf(at['res2'],lags = 40, ax=ax1)

باہر[70]:

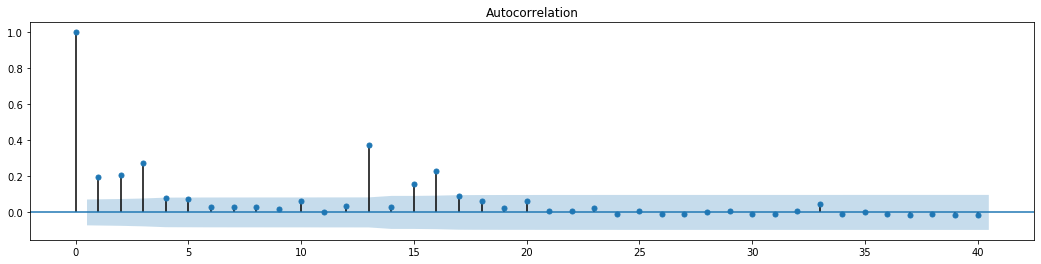
سیریز کے اختلاط ٹیسٹ کے لئے اصل مفروضہ یہ ہے کہ سیریز کا کوئی تعلق نہیں ہے۔ یہ دیکھا جاسکتا ہے کہ اعداد و شمار کے پہلے 20 احکامات کی متعلقہ P اقدار 0.05٪ اعتماد کی سطح کی اہم قیمت سے کم ہیں۔ لہذا ، اصل مفروضہ مسترد کردیا گیا ہے ، یعنی سیریز کے بقیہ کا اثر آرچ ہے۔ متغیر ماڈل کو باقی سیریز کی ہیٹروسکیڈاسٹیسیٹی کو فٹ کرنے اور مزید اتار چڑھاؤ کی پیش گوئی کرنے کے لئے آرچ ٹائپ ماڈل کے ذریعہ قائم کیا جاسکتا ہے۔

6. GARCH ماڈلنگ

گارچ ماڈلنگ کرنے سے پہلے ، ہمیں سیریز کے موٹے دم کے حصے سے نمٹنے کی ضرورت ہے۔ کیونکہ مفروضے میں سیریز کی غلطی کی اصطلاح کو معمول کی تقسیم یا ٹی تقسیم کے مطابق ہونے کی ضرورت ہے ، اور ہم نے پہلے تصدیق کی ہے کہ پیداوار سیریز میں موٹی دم کی تقسیم ہے ، لہذا ہمیں اس حصے کی وضاحت اور تکمیل کرنے کی ضرورت ہے۔

گارچ ماڈلنگ میں ، غلطی کا آئٹم عام تقسیم ، ٹی تقسیم ، جی ای ڈی (عام غلطی کی تقسیم) تقسیم اور اسکویڈ اسٹوڈنٹس ٹی تقسیم کے اختیارات فراہم کرتا ہے۔ اے آئی سی کے معیار کے مطابق ، ہم تمام اختیارات کے نتائج کا موازنہ کرنے کے لئے گنتی مشترکہ رجعت تخمینہ استعمال کرتے ہیں ، اور جی کی بہترین میچنگ ڈگری حاصل کرتے ہیں۔

متعلقہ

مزید