Bayes - Giải mã bí ẩn về xác suất, khám phá sự khôn ngoan toán học đằng sau việc ra quyết định
Tác giả:FMZ~Lydia, Tạo: 2023-11-27 11:55:42, Cập nhật: 2024-01-01 12:20:59
Thống kê Bayesian là một môn học mạnh mẽ trong lĩnh vực toán học, có ứng dụng rộng rãi trong nhiều lĩnh vực bao gồm tài chính, nghiên cứu y tế và công nghệ thông tin. Nó cho phép chúng ta kết hợp niềm tin trước với bằng chứng để dẫn ra những niềm tin mới, cho phép chúng ta đưa ra những quyết định khôn ngoan hơn.
Trong bài viết này, chúng tôi sẽ giới thiệu một số nhà toán học chính đã thành lập lĩnh vực này.
Trước Bayes
Để hiểu rõ hơn về số liệu thống kê Bayesian, chúng ta cần quay lại thế kỷ 18 và tham khảo nhà toán học De Moivre và bài báo của ông
Trong bài báo của mình, De Moivre đã giải quyết nhiều vấn đề liên quan đến xác suất và cờ bạc trong thời đại của mình.
Một trong những câu hỏi đơn giản nhất trong bài báo của ông là:
Đọc qua các vấn đề được mô tả trong
Điều này sẽ được thể hiện trong các thuật ngữ toán học như sau:
Công thức
𝑃(𝑋|𝜃)
Tuy nhiên, nếu chúng ta không biết nếu đồng xu là công bằng?𝜃 ?
Thomas Bayes và Richard Price
Gần năm mươi năm sau, vào năm 1763, một bài báo có tựa đề
Trong vài trang đầu tiên của tài liệu này, có một bài viết được viết bởi nhà toán học Richard Price tóm tắt một bài báo mà người bạn của ông Thomas Bayes đã viết vài năm trước khi ông qua đời.
Trên thực tế, ông đã đề cập đến một vấn đề cụ thể:
Nói cách khác, sau khi quan sát một sự kiện chúng ta xác định xác suất mà một tham số không rõθĐây thực sự là một trong những vấn đề đầu tiên liên quan đến suy luận thống kê trong lịch sử và nó đã tạo ra thuật ngữ xác suất nghịch chiều.
Công thức
𝑃( 𝜃 | 𝑋)
Đây tất nhiên là những gì chúng ta gọi là sự phân bố phía sau của định lý Bayes
Vì lý do không có nguyên nhân và hậu quả
Hiểu được động cơ đằng sau nghiên cứu của hai mục sư lớn tuổi này,Thomas BayesvàRichard PriceNhưng để làm điều này, chúng ta cần tạm thời bỏ qua một số kiến thức về thống kê.
Chúng ta đang ở trong thế kỷ 18 khi xác suất đang trở thành một lĩnh vực ngày càng thú vị cho các nhà toán học. Các nhà toán học như de Moivre hoặc Bernoulli đã cho thấy rằng một số sự kiện xảy ra với một mức độ ngẫu nhiên nhất định nhưng vẫn được quản lý bởi các quy tắc cố định. Ví dụ, nếu bạn ném xúc xắc nhiều lần, một phần sáu thời gian nó sẽ rơi vào sáu. Nó như thể có một quy tắc ẩn xác định cơ hội số phận.
Bây giờ hãy tưởng tượng bạn là một nhà toán học và một tín đồ sùng đạo sống trong thời kỳ này. Bạn có thể quan tâm đến việc hiểu mối quan hệ giữa quy luật ẩn này và Đức Chúa Trời.
Đây thực sự là câu hỏi được đặt ra bởi Bayes và Price. Họ hy vọng rằng giải pháp của họ sẽ trực tiếp áp dụng để chứng minh rằng thế giới phải là kết quả của trí tuệ và trí thông minh; do đó cung cấp bằng chứng cho sự tồn tại của Thiên Chúa như là nguyên nhân cuối cùng - nghĩa là nguyên nhân không có nhân quả.
Laplace
Đáng ngạc nhiên, khoảng hai năm sau đó vào năm 1774, mà không đọc bài báo của Thomas Bayes, nhà toán học người Pháp Laplace đã viết một bài báo có tựa đề "Về các nguyên nhân của sự kiện bằng xác suất của sự kiện", về các vấn đề xác suất nghịch chiều.
Đây là những gì chúng ta biết ngày nay là định lý Bayes:
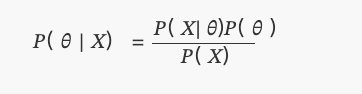
Ở đâu?P(θ)là một sự phân bố đồng đều.
Thử nghiệm tiền xu
Chúng ta sẽ mang lại thống kê Bayesian đến hiện tại bằng cách sử dụng Python và PyMC thư viện, và tiến hành một thí nghiệm đơn giản.
Giả sử một người bạn đưa cho bạn một đồng xu và hỏi bạn có nghĩ rằng nó là một đồng xu công bằng không. Bởi vì anh ta vội vàng, anh ta nói với bạn rằng bạn chỉ có thể ném đồng xu 10 lần. Như bạn có thể thấy, có một tham số không rõptrong vấn đề này, đó là xác suất của việc nhận được đầu trong ném đồng xu, và chúng tôi muốn ước tính giá trị có khả năng nhất củap.
(Lưu ý: Chúng tôi không nói rằng tham sốplà một biến ngẫu nhiên nhưng thay vào đó tham số này là cố định; chúng tôi muốn biết nơi nó có khả năng nhất giữa.)
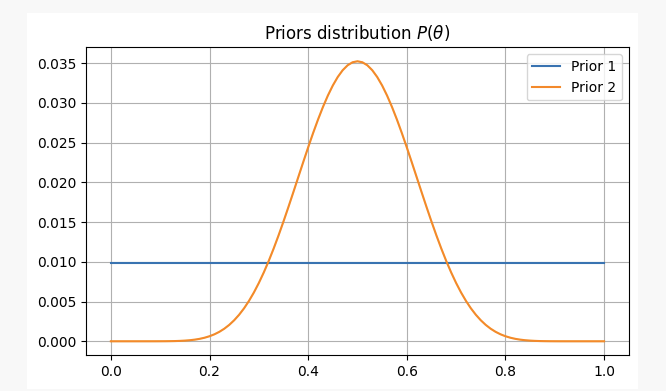
Để có những quan điểm khác nhau về vấn đề này, chúng ta sẽ giải quyết nó theo hai niềm tin trước đây khác nhau:
-
- Bạn không có thông tin trước về sự công bằng của đồng xu, vì vậy bạn gán một xác suất bằng nhau để
pTrong trường hợp này, chúng tôi sẽ sử dụng những gì được gọi là không thông tin trước bởi vì bạn đã không thêm bất kỳ thông tin nào cho niềm tin của bạn.
- Bạn không có thông tin trước về sự công bằng của đồng xu, vì vậy bạn gán một xác suất bằng nhau để
-
- Từ kinh nghiệm của bạn, bạn biết rằng ngay cả khi một đồng xu có thể không công bằng, nó là khó để làm cho nó cực kỳ không công bằng.
pkhông có khả năng là nhỏ hơn 0,3 hoặc lớn hơn 0,7. trong trường hợp này, chúng tôi sẽ sử dụng một thông tin trước.
- Từ kinh nghiệm của bạn, bạn biết rằng ngay cả khi một đồng xu có thể không công bằng, nó là khó để làm cho nó cực kỳ không công bằng.
Đối với hai kịch bản này, niềm tin trước đây của chúng ta sẽ như sau:
Với bằng chứng này, chúng ta có thể tìm thấy tham số của chúng ta ở đâup?
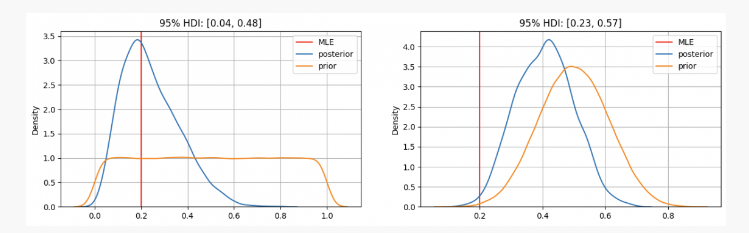
Như bạn có thể thấy, trong trường hợp đầu tiên, phân bố trước của chúng tôi của tham sốptập trung ở ước tính xác suất tối đa (MLE)p=0.2, đó là một phương pháp tương tự như phương pháp được sử dụng bởi trường tần số.
Mặt khác, trong những trường hợp có độ tin cậy cao rằng tham sốpTrong trường hợp này, tham số không rõ thực sự sẽ nằm trong khoảng độ tin cậy 95% giữa 0,23 và 0,57.
Vì vậy, trong trường hợp đầu tiên, bạn sẽ nói với bạn bè của bạn với sự chắc chắn rằng đồng tiền này không công bằng nhưng trong một tình huống khác, bạn sẽ nói rằng bạn không chắc chắn liệu nó có công bằng hay không.
Như bạn có thể thấy ngay cả khi phải đối mặt với bằng chứng giống hệt nhau (hai đầu trong mười lần ném), dưới các niềm tin trước khác nhau, kết quả có thể thay đổi rất nhiều; một lợi thế của thống kê Bayesian so với các phương pháp truyền thống nằm ở đây: giống như phương pháp khoa học, nó cho phép chúng ta cập nhật niềm tin của mình bằng cách kết hợp chúng với các quan sát và bằng chứng mới.
Kết thúc
Trong bài viết hôm nay, chúng ta đã xem nguồn gốc của thống kê Bayesian và những người đóng góp chính của nó. Sau đó, đã có nhiều người đóng góp quan trọng khác cho lĩnh vực thống kê này (Jeffreys, Cox, Shannon và vân vân), được tái in từ quantdare.com.
- FMZ định lượng: Các nhu cầu phổ biến của thị trường tiền điện tử
- WexApp, FMZ Quant Cryptocurrency Demo Exchange, vừa được ra mắt
- Giải thích chi tiết về tối ưu hóa tham số chiến lược lưới hợp đồng vĩnh viễn
- Dạy bạn sử dụng FMZ Extended API để Batch Modify Parameters của bot
- Dạy bạn sử dụng FMZ Extension API để thay đổi số lượng các tham số ổ đĩa
- Phương pháp tối ưu hóa các tham số lưới hợp đồng bền vững
- Hướng dẫn cài đặt Interactive Brokers IB Gateway trong Linux Bash
- Định hướng cài đặt chứng khoán xâm nhập IB GATEWAY trên Linux bash
- Điều gì phù hợp hơn cho việc đánh cá dưới đáy, giá trị thị trường thấp hay giá thấp?
- Giá trị thị trường thấp hay giá thấp, cái nào thích hợp hơn?
- Bayes - Bí mật giải mã xác suất, khám phá trí tuệ toán học đằng sau quyết định
- Những lợi thế của việc sử dụng API mở rộng của FMZ để quản lý kiểm soát nhóm hiệu quả trong giao dịch định lượng
- Hiệu suất giá sau khi đồng tiền được niêm yết trên các hợp đồng vĩnh viễn
- Sử dụng API mở rộng của FMZ để quản lý kiểm soát nhóm hiệu quả để có lợi trong giao dịch định lượng
- Giá của đồng tiền sau khi ký hợp đồng vĩnh cửu
- Sự tương quan giữa sự tăng và giảm của tiền tệ và Bitcoin
- Sự liên quan của Bitcoin với sự sụt giảm của đồng tiền
- Một cuộc thảo luận ngắn gọn về cán cân sổ lệnh trong các sàn giao dịch tập trung
- Đánh giá rủi ro và lợi nhuận - Giới thiệu về lý thuyết Markowitz
- Nói chuyện về cân bằng sổ lệnh của sàn giao dịch tập trung