Trong bài viết này, chúng ta sẽ tóm tắt quá trình Ornstein-Uhlenbeck, mô tả các công thức toán học của nó, thực hiện và mô phỏng nó bằng Python và thảo luận về một số ứng dụng thực tế trong tài chính định lượng và giao dịch hệ thống. Chúng ta sẽ sử dụng một mô hình quá trình ngẫu nhiên cao cấp hơn, được gọi là quá trình Ornstein-Uhlenbeck (OU), mô hình này có thể được sử dụng để mô hình hóa các chuỗi thời gian hồi quy thể hiện hành vi thu hồi giá trị bình đẳng.

Quá trình Ornstein-Uhlenbeck là gì?

Quá trình Ornstein-Uhlenbeck là một quá trình ngẫu nhiên theo thời gian liên tục được sử dụng để mô hình hóa hành vi thu hồi giá trị trung bình. Điều này có nghĩa là, không giống như sự trôi dạt ngẫu nhiên tiêu chuẩn hoặc chuyển động Brown có thể trôi dạt vô hạn, quá trình OU thường phục hồi về trung bình lâu dài theo thời gian. Về mặt toán học, quá trình OU là giải pháp cho các phương trình vi phân ngẫu nhiên cụ thể (SDE) điều khiển hành vi thu hồi giá trị trung bình này.

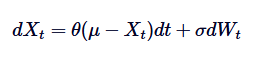
Trong đó, Xt biểu thị quá trình ngẫu nhiên trong thời gian t, μ là trung bình dài, θ là tỷ lệ trung bình, δ là biến động, và dWt là quá trình Wiener hoặc chuyển động Brown tiêu chuẩn.

Tiền bối lịch sử và ứng dụng

Quá trình Ornstein-Uhlenbeck ban đầu được đề xuất bởi Leonard Ornstein và George Eugene Uhlenbeck vào năm 1930 để mô phỏng tốc độ của các hạt trong chuyển động Brownian trong trường hợp có ma sát. Theo thời gian, tính thực tiễn của nó đã vượt xa vật lý và được áp dụng trong các lĩnh vực khác nhau như sinh học, hóa học, kinh tế và tài chính.

Trong tài chính định lượng, quá trình OU đặc biệt hữu ích trong việc mô hình hóa các hiện tượng thể hiện hành vi quay trở về giá trị trung bình. Các ví dụ nổi bật bao gồm sự biến động của lãi suất, tỷ giá hối đoái và thị trường tài chính. Ví dụ, mô hình lãi suất phổ biến mô hình Vasicek được đưa ra trực tiếp từ quá trình OU.

Tầm quan trọng trong tài chính định lượng

Quá trình Ornstein-Uhlenbeck rất quan trọng trong tài chính định lượng vì lý do sau đây. Tính chất trung bình của nó làm cho nó trở thành sự lựa chọn tự nhiên cho các biến số tài chính mô hình, các biến số tài chính này không thể hiện hành vi di chuyển ngẫu nhiên mà thay vào đó dao động xung quanh trung bình ổn định trong thời gian dài. Tính năng này rất quan trọng đối với mô hình lãi suất, trong đó trung bình trở lại phản ánh tác động của ngân hàng trung ương đối với lãi suất ổn định trong thời gian dài.

Ngoài ra, quá trình OU còn được sử dụng trong các mô hình định giá tài sản (bao gồm cả định giá các sản phẩm phái sinh) và các chiến lược quản lý rủi ro. Nó cũng có thể được sử dụng như một khối xây dựng cho các mô hình phức tạp hơn, chẳng hạn như mô hình Cox-Ingersoll-Ross (CIR), mô hình mở rộng quá trình OU để mô hình lãi suất không âm tính.

Đặc điểm chính và trực giác

Các đặc điểm chính của quá trình Ornstein-Uhlenbeck có thể được tóm tắt như sau:

• Phản hồi trung bình:Quá trình OU có xu hướng quay trở lại giá trị trung bình dài hạn μ. Điều này trái ngược hoàn toàn với các quá trình như chuyển động Brown, mà không có xu hướng này.
• Sự biến động:Mức độ ngẫu nhiên hoặc biến động trong quá trình điều khiển tham số δ. Sự biến động càng cao, quá trình càng lệch khỏi giá trị trung bình trước khi quay trở lại.
• Tốc độ trở về:Các tham sốθ quyết định tốc độ quay trở lại trung bình của quá trình.
• Sự ổn định:Quá trình OU là ổn định, có nghĩa là tính thống kê của nó không thay đổi theo thời gian. Điều này rất quan trọng trong việc mô hình hóa các hệ thống ổn định trong lĩnh vực tài chính.

Theo trực quan, bạn có thể xem quá trình Ornstein-Uhlenbeck như mô hình hóa hành vi của một sợi nhựa kéo quanh giá trị trung bình. Mặc dù quá trình này có thể bị lệch khỏi giá trị trung bình do dao động ngẫu nhiên, nhưng sợi nhựa kéo của sợi nhựa (cũng tương tự như sự quay trở lại giá trị trung bình) đảm bảo rằng nó cuối cùng sẽ quay trở lại giá trị trung bình.

So sánh với các quá trình ngẫu nhiên khác

Vì quá trình OU có liên quan chặt chẽ đến việc mô hình hóa các hiện tượng tài chính khác nhau, nó thường được so sánh với các quá trình ngẫu nhiên khác (như chuyển động Brown và chuyển động Brown hình học (GBM)). Không giống như chuyển động Brown (chuyển động Brown không có xu hướng quay trở lại trung bình), quá trình OU có hành vi quay trở lại trung bình rõ ràng. Điều này làm cho nó phù hợp hơn cho việc mô hình hóa các tình huống biến động xung quanh sự dao động cân bằng ổn định.

So với GBM, thường được sử dụng để mô hình hóa giá cổ phiếu và bao gồm các mục trôi dạt và dao động, quá trình OU không thể hiện sự tăng trưởng theo chỉ số, mà dao động xung quanh giá trị trung bình của nó. GBM thích hợp hơn để mô hình hóa số lượng tăng theo thời gian, trong khi quá trình OU rất thích hợp để mô hình hóa các biến thể thể hiện tính năng quay trở về giá trị trung bình.

Ví dụ về tài chính định lượng

Quá trình Ornstein-Uhlenbec có nhiều ứng dụng trong lĩnh vực tài chính, đặc biệt là trong các tình huống mô hình với phương tiện trở lại như một đặc điểm quan trọng. Dưới đây, chúng ta sẽ thảo luận về một số trường hợp sử dụng phổ biến nhất.

Mô hình lãi suất

Một trong những ứng dụng nổi bật nhất của quá trình OU là mô hình lãi suất, đặc biệt là trong khuôn khổ mô hình Vasicek. Mô hình Vasicek giả định lãi suất tuân theo quá trình OU, tức là lãi suất thường quay trở lại trung bình dài hạn theo thời gian. Đặc điểm này rất quan trọng để mô phỏng chính xác hành vi lãi suất, vì lãi suất thường không dao động vô hạn, mà dao động gần mức trung bình do điều kiện kinh tế ảnh hưởng.

Giá trị tài sản

Trong định giá tài sản, đặc biệt là các chứng khoán thu nhập cố định, quá trình OU thường được sử dụng để mô phỏng sự phát triển của tỷ lệ lợi nhuận trái phiếu. Bản chất quay trở về giá trị trung bình của quá trình OU đảm bảo tỷ lệ lợi nhuận không đi quá xa so với giá trị trung bình lịch sử của nó, phù hợp với hành vi thị trường được quan sát. Điều này làm cho quá trình OU trở thành một công cụ quý giá để định giá trái phiếu và các công cụ nhạy cảm với lãi suất khác.

Chiến lược giao dịch cặp

Giao dịch cặp là một chiến lược trung lập thị trường liên quan đến việc thiết lập một vị trí cân bằng giữa hai tài sản liên quan. Trong trường hợp này, quá trình OU đặc biệt hữu ích vì nó có thể mô hình hóa chênh lệch giá giữa hai tài sản, và chênh lệch giá thường là sự đảo ngược trung bình. Bằng cách sử dụng quá trình OU để mô hình hóa chênh lệch giá, các nhà giao dịch có thể xác nhận điểm vào và thoát lợi nhuận khi giá lệch khỏi giá trị trung bình của nó, dự đoán sự đảo ngược trung bình, và do đó tạo ra tín hiệu giao dịch.

Ví dụ, nếu chênh lệch giá giữa hai hợp đồng tương lai mở rộng vượt quá một mức giảm giá nào đó, các nhà giao dịch có thể bỏ qua hợp đồng tương lai hoạt động tốt và mua nhiều hợp đồng tương lai hoạt động kém, hy vọng rằng chênh lệch giá sẽ trở lại mức trung bình lịch sử của nó, do đó thu lợi nhuận khi sự đảo ngược xảy ra.

Giải pháp của Ornstein-Uhlenbeck SDE

Công thức phương trình phân số của quá trình Ornstein-Uhlenbeck là cơ sở để giải SDE này. Để giải SDE này, chúng tôi sử dụng phương pháp nhân tích. Hãy viết lại SDE:

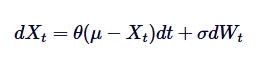
Đầu tiên, chúng ta nhân cả hai bên bằng nhân tích /upload/asset/28dfe9abfb54772651590.png:

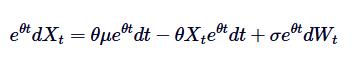
Lưu ý rằng nếu chúng ta thêm 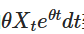ở cả hai bên, thì bên trái có thể được thể hiện là sự chênh lệch của nhân:

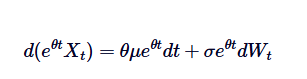
Nếu chúng ta tích hợp cả hai bên từ 0 đến t, chúng ta sẽ có:

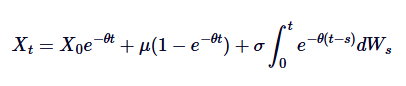
Đây là giải thích chung của Ornstein-Uhlenbeck SDE.

Giải pháp hiển thị được đưa ra ở trên có một số ý nghĩa quan trọng. Thứ nhất 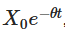cho thấy giá trị ban đầu suy giảm theo thời gian, cho thấy quá trình dần dần quên đi điểm bắt đầu của nó. Thứ hai 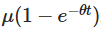cho thấy quá trình theo thời gian hướng đến giá trị trung bình của μ. Điều thứ ba giới thiệu tính ngẫu nhiên, trong đó tích hợp quá trình của Wiener giải thích sự biến động ngẫu nhiên.

Giải pháp này nhấn mạnh sự cân bằng giữa hành vi hồi quy trung bình xác định và tỷ lệ ngẫu nhiên theo động tác Brownian. Hiểu giải pháp này là rất quan trọng để mô phỏng hiệu quả quá trình OU, như sau:

Liên kết với các quá trình ngẫu nhiên khác

Quá trình Ornstein-Uhlenbeck có một số liên kết quan trọng với các quá trình ngẫu nhiên nổi tiếng khác (bao gồm cả chuyển động Brown và mô hình Vasicek).

Mối quan hệ với phong trào Brown

Quá trình Ornstein-Uhlenbeck có thể được xem như là một phiên bản hồi trung bình của chuyển động Brown. Phong trào Brown mô tả một quá trình có xu hướng tăng độc lập mà không có hồi trung bình, trong khi quá trình OU giới thiệu hồi trung bình bằng cách sử dụng các điều khoản trôi dạt để sửa đổi chuyển động Brown, do đó kéo quá trình trở lại giá trị trung tâm. Về mặt toán học, nếu chúng ta đặtθ = 0, quá trình OU sẽ được rút gọn thành chuyển động Brown tiêu chuẩn với các bước dao động:

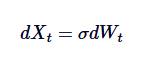
Do đó, chuyển động của Brown là một trường hợp đặc biệt của quá trình OU, tương ứng với sự thiếu hụt của sự hồi phục trung bình.

Quan hệ với mô hình Vasicek

Mô hình Vasicek được sử dụng rộng rãi trong mô hình lãi suất, về cơ bản là ứng dụng của quá trình Ornstein-Uhlenbeck trong sự tiến hóa lãi suất. Mô hình Vasicek giả định lãi suất tuân theo quá trình OU, trong đó SDE được định nghĩa là:

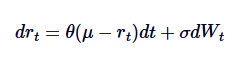
Trong đó, rt biểu thị lãi suất ngắn hạn, giải thích tham sốθ,μ vàδ tương tự như giải thích trong quá trình OU. Mô hình Vasicek có thể tạo ra đường dẫn lãi suất trung bình, đây là một trong những lợi thế chính của nó trong mô hình hóa tài chính.

Hiểu được các mối quan hệ này có thể giúp hiểu rõ hơn về cách thức sử dụng quy trình OU trong các môi trường khác nhau, đặc biệt là trong lĩnh vực tài chính. Chúng ta sẽ tìm hiểu ý nghĩa thực tế của các mối quan hệ này khi thảo luận về các ví dụ ứng dụng dưới đây.

Phương thức Ornstein-Uhlenbeck mô phỏng bằng Python

Trong phần này, chúng ta sẽ tìm hiểu cách sử dụng Python để mô phỏng quá trình Ornstein-Uhlenbeck (OU). Điều này liên quan đến phương trình phân tích ngẫu nhiên định nghĩa quá trình OU (SDE) bằng cách phân tách Euler-Maruyama.

Sự phân tán của SDE

Chúng ta hãy xem lại các công thức toán học của SDE ở trên và tóm tắt từng thuật ngữ:

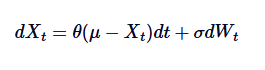
TRONG,

• Xt là giá trị của quá trình trong thời gian t.
• θ là tốc độ quay trở về giá trị trung bình
• μ là trung bình thời gian của quá trình.
• δ là tham số tỷ lệ dao động.
• dWt biểu thị sự gia tăng của quá trình Wiener ((chuyển động Brown tiêu chuẩn)).

Để mô phỏng quá trình này trên máy tính, chúng ta cần phân ly SDE thời gian liên tục. Một phương pháp thường được sử dụng là phân ly Euler-Maruyama, nó xấp xỉ quá trình liên tục bằng cách tính đến bước thời gian phân ly nhỏ.

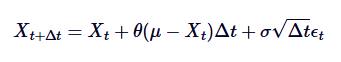
Trong đó, 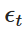là một biến ngẫu nhiên được rút ra từ phân phối chính xác tiêu chuẩn (tức là 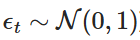). Sự phân tách này cho phép chúng ta tính toán giá trị của Xt theo thời gian để mô phỏng hành vi của quá trình OU.

Thực hiện Python

Bây giờ chúng ta hãy sử dụng Python để thực hiện quá trình Ornstein-Uhlenbeck phân tách. Trong phần này, chúng ta chỉ sử dụng thư viện Python NumPy và Matplotlib.

Đầu tiên, chúng ta nhập NumPy và Matplotlib theo cách tiêu chuẩn. Sau đó, chúng ta chỉ định tất cả các tham số cho mô hình OU. Sau đó, chúng ta phân bổ trước một mảng NumPy có chiều dài N để thêm vào nó sau khi tính toán đường OU. Sau đó chúng ta lặp N-1 (bước 1 là điều kiện ban đầu được chỉ định X0), mô phỏng gia tăng ngẫu nhiên dW, sau đó tính toán lần lặp tiếp theo của đường OU theo công thức toán học trên.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Kết quả của bản vẽ là như sau:

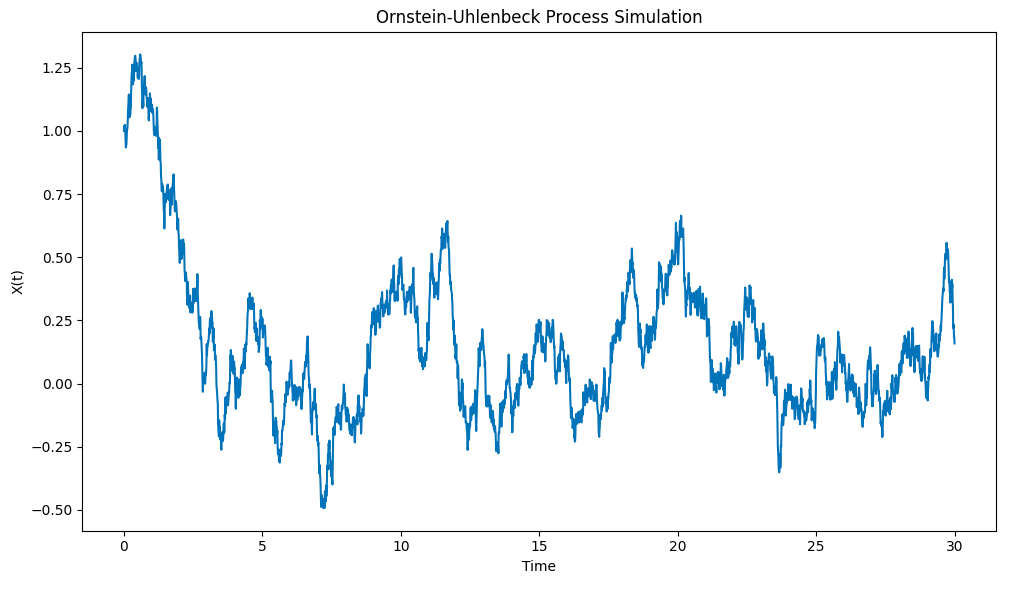
Mô phỏng quá trình Ornstein-Uhlenbeck được vẽ bằng Python

Lưu ý rằng quá trình này có thể nhanh chóng kéo từ điều kiện ban đầu đến trung bình khi X0 = 1 đến trung bình khi μ = 0 và sau đó nó cho thấy xu hướng quay trở lại trung bình khi nó lệch khỏi trung bình.

Tóm tắt và các bước tiếp theo

Trong bài viết này, chúng tôi đã giới thiệu quá trình Ornstein-Uhlenbeck, mô tả các công thức toán học của nó và cung cấp các triển khai cơ bản của Python để mô phỏng các phiên bản phân tách của SDE liên tục. Trong bài viết tiếp theo, chúng tôi sẽ nghiên cứu các SDE phức tạp hơn được xây dựng dựa trên quá trình OU và xem chúng được sử dụng như thế nào cho các ứng dụng giao dịch hệ thống và định giá dẫn xuất.

Mã đầy đủ

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Các bài viết khác về Python: http://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python