Công thức Kelly - một công cụ mạnh mẽ để kiểm soát vị trí

** Giả sử: Bạn có 60% khả năng thắng và 40% khả năng thua. Lợi nhuận ròng khi thắng là 100% và lỗ khi thua là 100%. Tức là, nếu thắng, bạn có thể giành được 1 đô la cho mỗi đô la, và nếu thua, bạn sẽ mất 1 đô la cho mỗi đô la.

• 1, đối với thế này, mỗi lần đặt cược sẽ có 60% lợi nhuận.*1-40%*1=20%, kỳ vọng lợi nhuận là tích cực. nghĩa là đây là một sự bế tắc đối với các hacker, và lợi thế rất lớn.

Vậy chúng ta nên đặt cược như thế nào?

Nếu không suy nghĩ nghiêm ngặt, chúng ta có thể nghĩ rằng nếu tôi có 20% lợi nhuận cho mỗi lần đánh bạc, thì để đạt được lợi nhuận tối đa trong thời gian dài, tôi nên cố gắng đặt một tỷ lệ số tiền thật nhiều hơn trong mỗi lần đánh bạc.

Nhưng rõ ràng mỗi lần đánh bạc đều đặt 100% vốn là không hợp lý, bởi vì một khi đánh bạc nào thua, tất cả vốn sẽ bị mất, không thể tham gia vào trận đấu tiếp theo, chỉ có thể rời khỏi trận đấu.

Vì vậy, kết luận là: nếu có một cơ hội để mất toàn bộ vốn ngay lập tức, dù là rất nhỏ, bạn sẽ không bao giờ có thể có đầy đủ. Bởi vì trong thời gian dài, các sự kiện có xác suất nhỏ nhất định sẽ xảy ra, và trong cuộc sống thực tế, xác suất thực tế của sự kiện có xác suất nhỏ sẽ lớn hơn nhiều so với xác suất lý thuyết của nó. Đây là hiệu ứng đuôi mỡ trong tài chính.

• 2/ Tiếp tục quay lại tình trạng bế tắc 1. Nếu mỗi lần đặt cược 100% là không hợp lý, vậy còn 99% thì sao? Nếu mỗi lần đặt cược 99% không chỉ đảm bảo bạn sẽ không bao giờ phá sản, mà nếu bạn may mắn, bạn có thể kiếm được rất nhiều lợi nhuận.

Đây có phải là thực tế hay không?

Chúng ta không phân tích vấn đề này theo lý thuyết, chúng ta có thể thực hiện một thí nghiệm. Chúng ta mô phỏng tình trạng bế tắc này, và đặt cược 99% mỗi lần để xem kết quả sẽ ra sao.

Đây là một thí nghiệm mô phỏng rất đơn giản, có thể thực hiện bằng Excel.

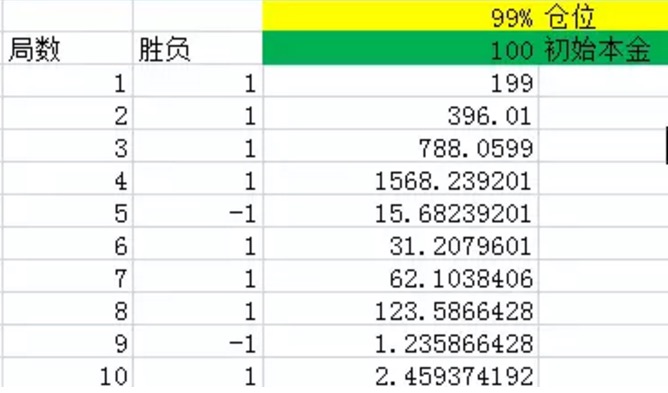Hình 1

Như trên, cột đầu tiên cho biết số lượt. Cột thứ hai là chiến thắng, excel sẽ tạo ra 1 theo xác suất 60%, tức là 60% xác suất lợi nhuận ròng là 1,40% xác suất -1, tức là 40% xác suất lợi nhuận ròng là -1. Cột thứ ba là tất cả tiền của người chơi khi kết thúc mỗi lượt.

Các bạn có thể thấy từ biểu đồ, sau khi thực hiện 10 lượt, số lượt thắng trong 10 lượt là 8, có xác suất lớn hơn 60% và chỉ thua hai lần. Nhưng ngay cả khi vậy, số tiền cuối cùng chỉ còn lại là 2.46 USD, về cơ bản là mất mát.

Và khi tôi tăng số lần thử nghiệm lên thành 1000, 2000, 3000… thì có thể thấy rằng cuối cùng, số tiền trong tay của tôi về cơ bản là 0.

Và vì 99% cũng không có tác dụng, chúng ta hãy thử một vài tỷ lệ khác, và hãy nhìn vào biểu đồ dưới đây: Từ biểu đồ có thể thấy rằng khi giảm dần vị thế, từ 99%, trở thành 90%, 80%, 70%, 60%, kết quả của cùng 10 lượt hoàn toàn khác nhau. Từ biểu đồ có vẻ như có thể thấy rằng số tiền sau 10 lượt dần dần lớn hơn khi vị trí dần dần nhỏ hơn.

Nếu bạn nhìn vào đây, bạn sẽ dần nhận ra rằng vấn đề của sự bế tắc này không đơn giản như vậy.

Vậy làm thế nào để đặt cược để có được lợi nhuận lớn nhất trong dài hạn?

Có phải tỉ lệ càng nhỏ càng tốt, như chúng ta thấy trên đây không?

Vậy tỷ lệ tối ưu là bao nhiêu?

Đây là vấn đề mà công thức nổi tiếng của Kelly phải giải quyết!

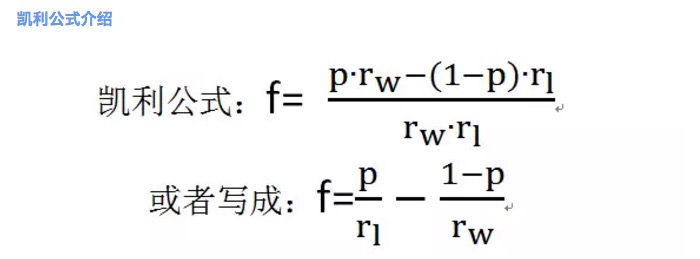Hình 2

trong đó f là tỷ lệ cược tối ưu; p là xác suất chiến thắng; rw là tỷ lệ lợi nhuận ròng khi chiến thắng, ví dụ như trong vòng 1 rw = 1; rl là tỷ lệ thua lỗ ròng, ví dụ như trong vòng 1 rl = 1; lưu ý ở đây rl> 0;

Theo công thức Kelly, tỷ lệ cược tối đa trong trò chơi 1 có thể được tính là 20%.

Chúng ta có thể thử nghiệm để hiểu rõ hơn về kết luận này.

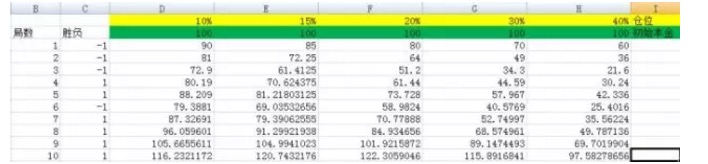Hình 3

Như trong hình, chúng ta đặt các vị trí là 10%, 15%, 20%, 30%, 40%; các cột tương ứng của chúng là D, E, F, G, H.

Và khi tôi thực hiện thử nghiệm 3000 lần, Và khi tôi thực hiện thử nghiệm này 5000 lần, Các bạn có thể thấy rằng kết quả của F là lớn nhất, so với các cột khác thì không phải là một số lượng. Trong khi đó, tỷ lệ vị trí của F tương ứng với 20% .

Các bạn đã thấy được sức mạnh của công thức Kelly rồi đấy. Trong thí nghiệm trên, nếu bạn không may chọn tỷ lệ là 40%, tức là H column, thì sau 5000 lượt đánh bạc, tiền của bạn sẽ tăng từ 100 lên 22799985.75, thu nhập rất lớn. Nhưng so với kết quả tỷ lệ 20% thì đó thực sự là không có tiền.

Đây là sức mạnh của kiến thức!

• 3, Hiểu rõ phương trình Kelly

Lý giải toán học của phương trình Kelly và sự phức tạp của nó đòi hỏi kiến thức toán học rất cao và sâu sắc, vì vậy không có ý nghĩa gì để thảo luận ở đây. Ở đây tôi sẽ thực hiện một số thí nghiệm để nâng cao sự hiểu biết chủ quan về phương trình Kelly.

Chúng ta hãy xem một trò chơi cờ bạc. Trò chơi cờ bạc 2: Bạn thua và thắng có xác suất 50%, ví dụ như ném đồng xu. Khi thắng, thu nhập ròng là 1, rw = 1, khi thua, thu nhập ròng là 0,5, rl = 0,5.

Có thể dễ dàng nhận thấy rằng lợi nhuận dự kiến của Băng 2 là 0.25, một Băng có lợi thế rất lớn của các nhà lừa đảo.

Theo công thức Kelly, tỷ lệ cược tối ưu cho mỗi lượt là:

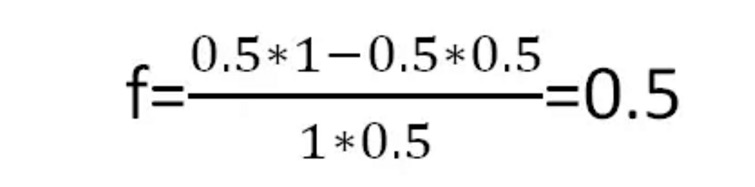Hình 4

Theo đó, mỗi lần bạn đặt cược một nửa số tiền của mình, bạn sẽ nhận được lợi nhuận lớn nhất trong thời gian dài.

Sau đây tôi sẽ đưa ra khái niệm về tốc độ tăng trưởng trung bình r dựa trên thí nghiệm.

Đầu tiên, hãy xem thử nghiệm 2.1 với hai biểu đồ sau:

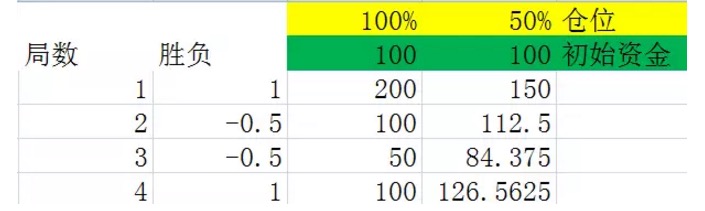Hình 5

Cả hai biểu đồ này đều là các thí nghiệm được thực hiện để mô phỏng Bán cược 2, trong hàng thứ hai, hàng thắng của thí nghiệm sẽ tạo ra 50% xác suất 1, đại diện cho lợi nhuận 100%. 50% xác suất tạo ra -0.5, đại diện cho tổn thất 50%.

So sánh cẩn thận hai biểu đồ có thể tìm thấy kết luận thứ nhất, đó là sau khi trải qua cùng một số lượt, kết quả cuối cùng chỉ liên quan đến số lượt thắng và số lượt thua trong các lượt này, không liên quan đến thứ tự thắng và thua trong các lượt này. Ví dụ, trong hai biểu đồ trước, cũng được thực hiện 4 lượt, cũng có hai lượt thắng và hai lượt thua trong mỗi biểu đồ, nhưng thứ tự thua của biểu đồ đầu tiên là thắng thua thắng, thứ tự thua của biểu đồ thứ hai là thua thua thắng thắng.

Tất nhiên, kết luận này rất dễ chứng minh ((hệ thống giao dịch phép nhân, học sinh tiểu học sẽ làm được), nhưng không chứng minh được ở đây, hai ví dụ trên đã đủ để mọi người hiểu rõ.

Vì kết quả cuối cùng không liên quan đến thứ tự thắng thua, chúng ta hãy giả định rằng Bán quyết 2 sẽ diễn ra như trong thí nghiệm 2.2, xem hình dưới đây:

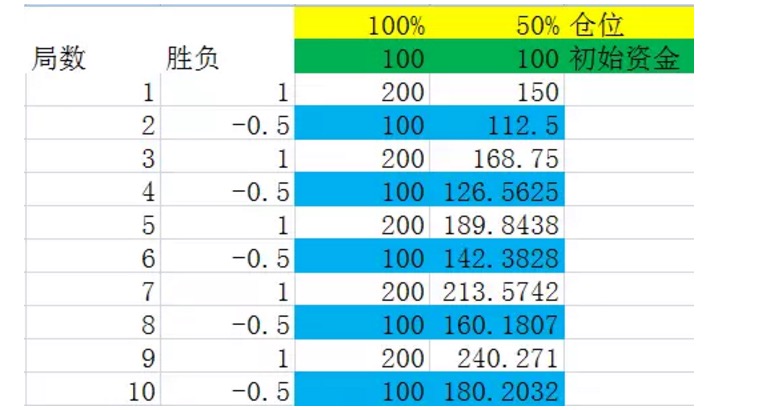Hình 6

Chúng ta giả định rằng các chiến thắng trong trận đấu là do sự thay đổi, vì kết luận thứ nhất, trong thời gian dài, điều này không ảnh hưởng gì đến kết quả.

Trước khi chúng ta nhìn vào hình ảnh, chúng ta hãy định nghĩa. Giả sử rằng một số trận đấu được coi là một toàn bộ, trong đó tần suất của các kết quả là chính xác bằng xác suất của nó, và số trận đấu của toàn bộ này là số trận đấu trung bình nhỏ nhất trong toàn bộ tất cả các điều kiện được đáp ứng, sau đó chúng ta gọi toàn bộ này là một nhóm trận đấu. Ví dụ như trong thí nghiệm trên, một nhóm trận đấu đại diện cho việc chơi hai trận đấu, trong đó thắng một lần thua.

Nhìn kỹ vào các con số được đánh dấu màu xanh trên biểu đồ, chúng là kết thúc của một nhóm ngưng trệ. Bạn sẽ thấy rằng các con số này tăng trưởng ổn định. Khi vị trí là 100%, con số được đánh dấu màu xanh là tăng trưởng 0%, tức là tăng trưởng vốn sau một nhóm ngưng trệ là 0%. Điều này cũng giải thích rằng khi mỗi lần đặt cược đầy đủ, trong vòng đấu 2 không thể kiếm tiền trong thời gian dài.

Đây là một quy luật phổ biến, tỷ lệ tăng sau mỗi nhóm đình trệ có liên quan đến vị trí. Và tỷ lệ tăng sau mỗi nhóm đình trệ càng lớn, lợi nhuận cuối cùng sẽ càng lớn về lâu dài.

Tỷ lệ tăng trưởng của mỗi nhóm có thể được tính toán dựa trên tỷ lệ tăng trưởng trung bình của mỗi nhóm g. Trong biểu đồ trên, mỗi nhóm bao gồm hai nhóm, thì tỷ lệ tăng trưởng trung bình của mỗi nhóm là

Hình 7

Trong dài hạn, để có được sự tăng trưởng lớn nhất của vốn, thực sự chỉ cần làm cho r lớn nhất, tức là để g tối đa. Và tỷ lệ cược tốt nhất f thực sự là do giải pháp max ((g)).

• Các kết luận khác về nguy cơ của công thức Kelly

Truyền thuyết Kelly

Công thức Kelly ban đầu được xây dựng cho John Larry Kelly, một nhà vật lý tại AT&T Bell Labs, dựa trên nghiên cứu của đồng nghiệp của ông, Claude Elwood Shannon về tin nhắn đường dây điện thoại đường dài. Kelly giải quyết vấn đề về cách áp dụng lý thuyết thông tin của Shannon đối với một kẻ đánh bạc có tin tức nội bộ trong lúc đánh bạc. Người đánh bạc muốn quyết định số tiền cược tốt nhất, và tin tức nội bộ của anh ta không cần phải hoàn hảo (không có tin tức), tức là cho anh ta một lợi thế hữu ích. Sau đó, Thorpe đã sử dụng thời gian làm việc của mình để viết một bài luận toán học có tựa đề Chiến lược chọn tốt nhất để đánh bạc 21 điểm. Ông đã sử dụng kiến thức của mình để tấn công tất cả các sòng bạc ở thành phố Reno, Nevada trong một đêm và đã giành được hàng chục ngàn đô la từ bàn đánh bạc 21 điểm. Ông cũng là cha đẻ của quỹ bảo hiểm giao dịch định lượng trên phố Wall, sáng lập quỹ bảo hiểm giao dịch định lượng đầu tiên vào những năm 70.

Sử dụng viễn cảnh

Làm thế nào để kiếm tiền trong cuộc sống thực bằng công thức Kelly? Đó là để tạo ra một tình trạng bế tắc đáp ứng các điều kiện của phương thức Kelly. Theo tôi, tình trạng bế tắc này phải đến từ thị trường tài chính. Một quy tắc mua bán với kỳ vọng lợi nhuận tích cực chiếm 10% tầm quan trọng, một phương pháp kiểm soát tài chính tốt chiếm 40% tầm quan trọng, và 50% còn lại là sự kiểm soát tâm lý của con người. Và công thức Kelly chính là công cụ giúp tôi kiểm soát vị thế tài chính của mình. Ví dụ như một hệ thống giao dịch chứng khoán mà tôi đã nghiên cứu trước đây, hệ thống này giao dịch một lần mỗi tuần, xác suất thành công của mỗi giao dịch là 0.8, xác suất thất bại là 0.2. Khi thành công, bạn có thể kiếm được 3% ((giảm hoa hồng, thuế in ấn), mỗi lần thất bại, mất 5% . Trước khi biết công thức Kelly, tôi là một giao dịch hoàn toàn mù quáng, cũng không biết tôi đặt vị trí này là không đúng, tâm lý rất ảo. Tất nhiên, phương thức Kelly không thể đơn giản như vậy trong ứng dụng thực tế, và có rất nhiều khó khăn cần phải vượt qua. Ví dụ như chi phí vốn cần thiết cho các sàn giao dịch đòn bẩy, ví dụ như tiền không có thể phân chia vô hạn trong thực tế, ví dụ như trong thị trường tài chính không đơn giản như tình trạng bế tắc đơn giản được đề cập ở trên. Nhưng dù sao đi nữa, công thức Kelly đã chỉ đường cho chúng ta.