Dự đoán giá Bitcoin trong thời gian thực với khuôn khổ LSTM

Xin lưu ý: Trường hợp này chỉ được sử dụng để nghiên cứu và không phải là một đề xuất đầu tư.

Dữ liệu giá của Bitcoin dựa trên chuỗi thời gian, do đó dự đoán giá của Bitcoin chủ yếu được thực hiện bằng mô hình LSTM.

Lưu ý ngắn hạn dài (LSTM) là một mô hình học sâu đặc biệt phù hợp với dữ liệu chuỗi thời gian (hoặc dữ liệu có thứ tự thời gian / không gian / cấu trúc, chẳng hạn như phim ảnh, câu nói, v.v.) và là mô hình lý tưởng để dự đoán xu hướng giá của tiền điện tử.

Bài viết này chủ yếu viết về việc kết hợp dữ liệu thông qua LSTM để dự đoán giá Bitcoin trong tương lai.

Import các thư viện cần sử dụng

import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Phân tích dữ liệu

Đang tải dữ liệu

Đọc dữ liệu giao dịch BTC hàng ngày

data = pd.read_csv(filepath_or_buffer="btc_data_day")

Hiện tại, có tổng cộng 1380 mục dữ liệu, bao gồm các hàng DATE, OPEN, HIGH, LOW, CLOSE, VOLUME (BTC), VOLUME (CURRENCY) và WEIGHTED PRICE.

data.info()

Xem số liệu trên 10 dòng dưới đây.

data.head(10)

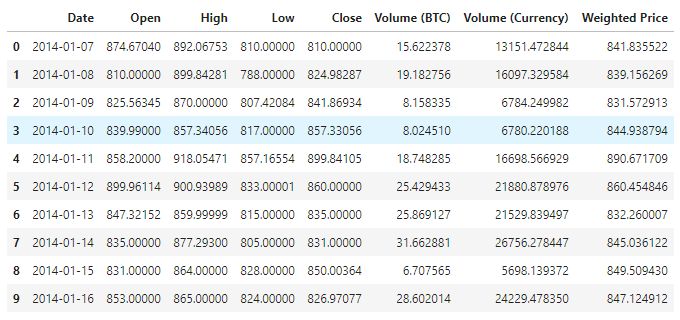
Hiển thị dữ liệu

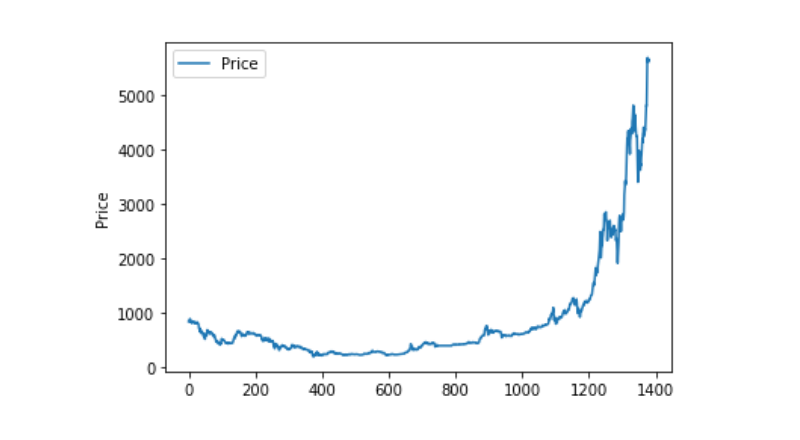
Sử dụng matplotlib để vẽ ra Weighted Price để xem sự phân bố và xu hướng của dữ liệu. Trong biểu đồ, chúng ta thấy một phần của dữ liệu 0 và chúng ta cần xác nhận liệu có bất thường nào trong dữ liệu dưới đây.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

Xử lý dữ liệu bất thường

Chúng ta hãy xem liệu dữ liệu có chứa dữ liệu nan hay không.

data.isnull().sum()

Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Và nếu chúng ta nhìn lại dữ liệu 0, chúng ta có thể thấy rằng dữ liệu của chúng ta có một giá trị 0, và chúng ta cần phải xử lý giá trị 0.

(data == 0).astype(int).any()

Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

(data == 0).astype(int).any()

Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Và khi chúng ta nhìn vào sự phân bố và xu hướng của dữ liệu, đường cong đã rất liên tục.

plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

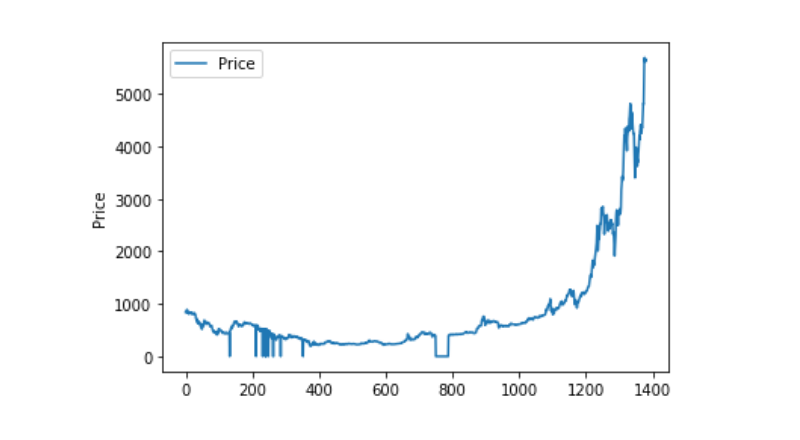
Phân loại tập dữ liệu huấn luyện và tập dữ liệu thử nghiệm

Kết hợp dữ liệu thành 0 - 1

data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Phân chia 2:8 giữa tập dữ liệu thử nghiệm và tập dữ liệu đào tạo

ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Tạo bộ dữ liệu huấn luyện và thử nghiệm với thời gian cửa sổ 1 ngày để tạo bộ dữ liệu huấn luyện và thử nghiệm của chúng tôi.

def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Định nghĩa mô hình và đào tạo

Lần này chúng ta sử dụng một mô hình đơn giản, cấu trúc mô hình như sau: 1. LSTM2.

Ở đây cần phải giải thích về hình thức đầu vào của LSTM, kích thước đầu vào của Input Shape là ((batch_size, time steps, features)). Trong đó, giá trị time steps là khoảng thời gian cửa sổ thời gian khi nhập dữ liệu, ở đây chúng ta sử dụng 1 ngày như một cửa sổ thời gian, và dữ liệu của chúng ta là dữ liệu ngày, vì vậy ở đây các bước thời gian của chúng ta là 1.

Long short-term memory (LSTM) là một loại RNN đặc biệt, chủ yếu để giải quyết các vấn đề biến mất gradient và nổ gradient trong quá trình đào tạo chuỗi dài.

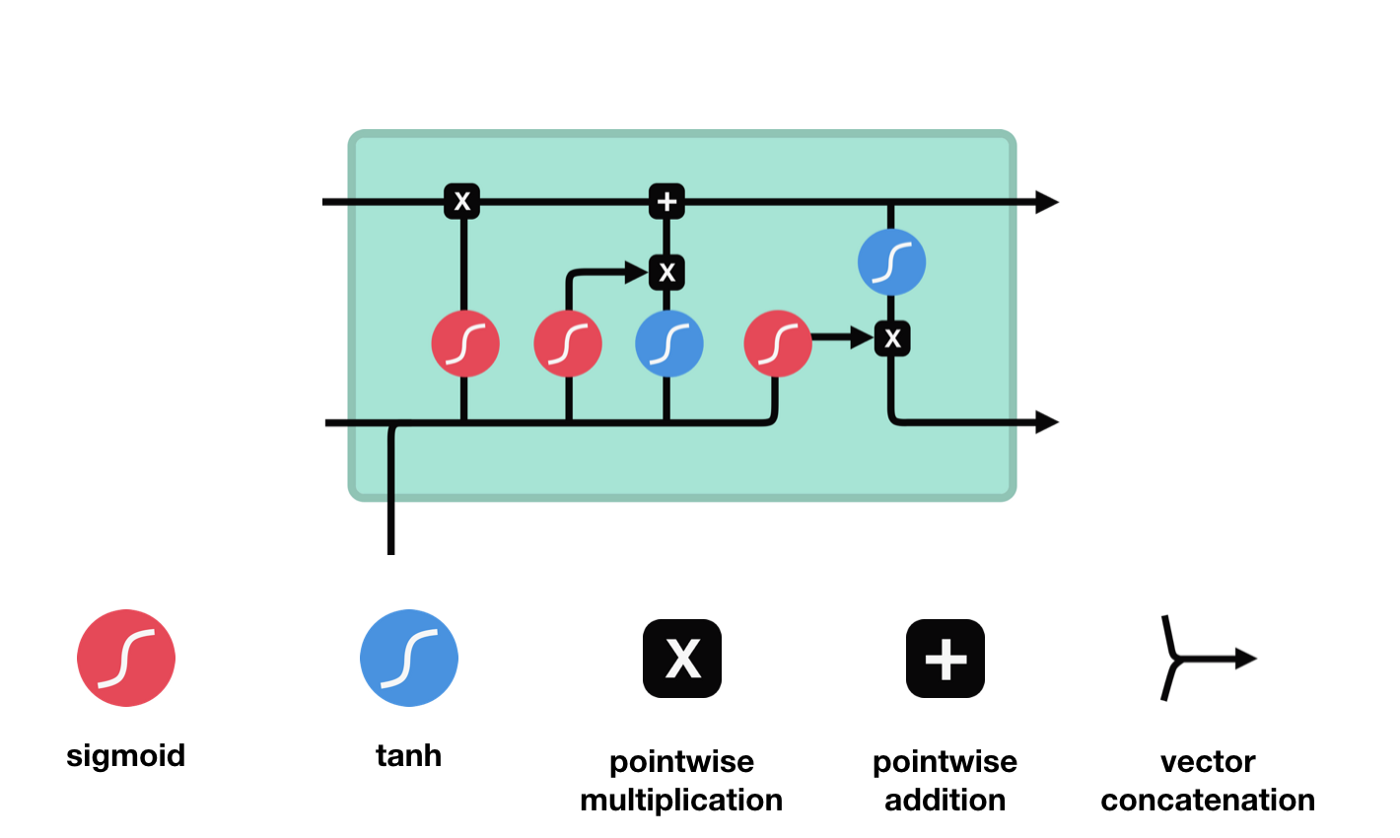
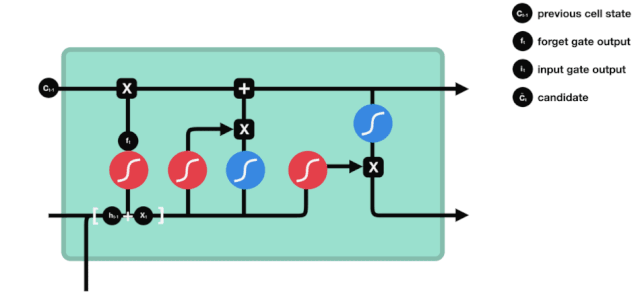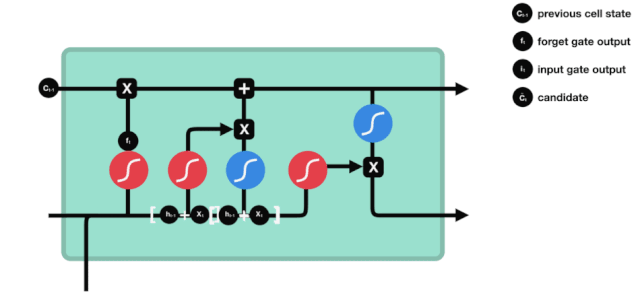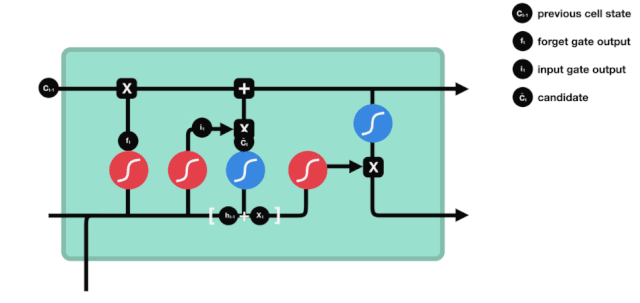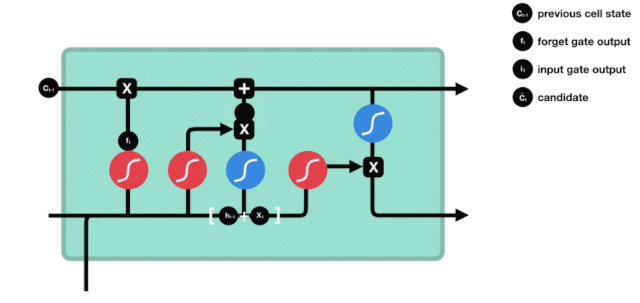
Từ biểu đồ cấu trúc mạng của LSTM, bạn có thể thấy rằng LSTM thực sự là một mô hình nhỏ, nó chứa 3 chức năng kích hoạt sigmoid, 2 chức năng kích hoạt tanh, 3 phép nhân, 1 phép cộng.

Tình trạng tế bào

Tình trạng tế bào là trung tâm của LSTM, ông là đường đen ở trên cùng của biểu đồ trên, và bên dưới đường đen là một số cửa, chúng tôi sẽ giới thiệu sau đây. Tình trạng tế bào sẽ được cập nhật dựa trên kết quả của mỗi cửa. Sau khi chúng tôi giới thiệu các cửa, bạn sẽ hiểu quá trình trạng thái tế bào.

Mạng lưới LSTM có thể xóa hoặc thêm thông tin về trạng thái tế bào thông qua một cấu trúc được gọi là cổng. Cổng có thể chọn lựa quyết định thông tin nào được truyền qua. cấu trúc của cổng là một sự kết hợp giữa một lớp sigmoid và một hoạt động nhân điểm.

Cánh cửa bị quên

Bước đầu tiên của LSTM là quyết định trạng thái tế bào cần loại bỏ thông tin nào. Phần này được xử lý bởi một đơn vị sigmoid gọi là cửa quên.

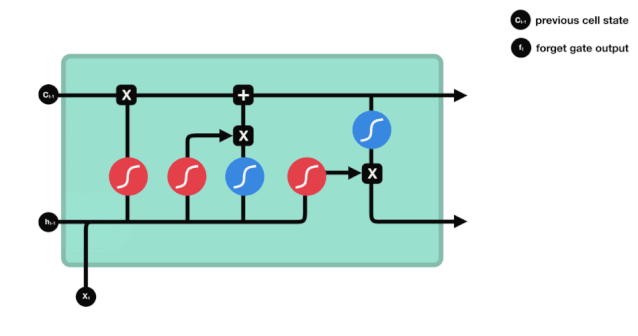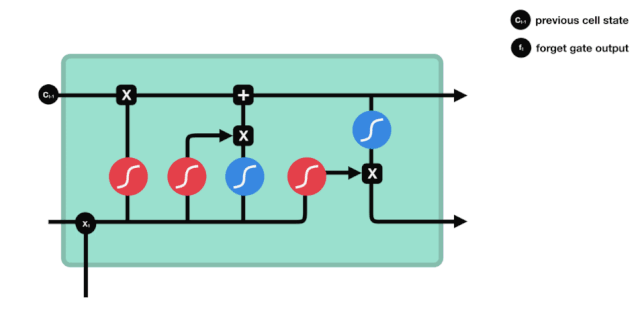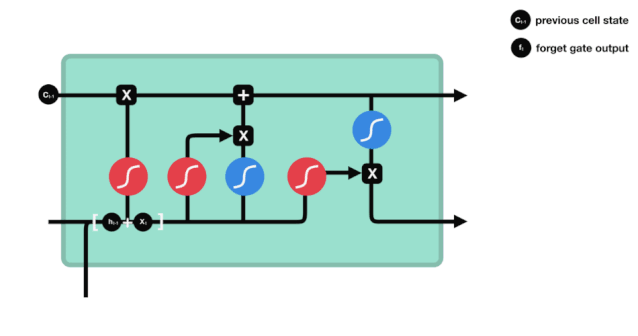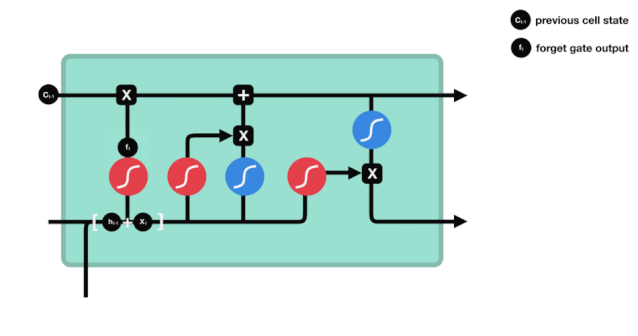
Chúng ta có thể thấy rằng cửa ngõ bị lãng quên xuất ra một vector giữa 0 - 1 bằng cách xem thông tin $h_{l-1} $ và $x_{t} $, trong đó giá trị 0 - 1 trong vector cho thấy thông tin nào trong trạng thái tế bào $C_{t-1} $ được giữ hoặc loại bỏ nhiều như thế nào.

biểu thức toán học: $f_{t}=\sigma\left ((W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) $

Cổng vào

Bước tiếp theo là quyết định những thông tin mới cần được thêm vào trạng thái tế bào, và bước này được thực hiện bằng cách mở cửa nhập.

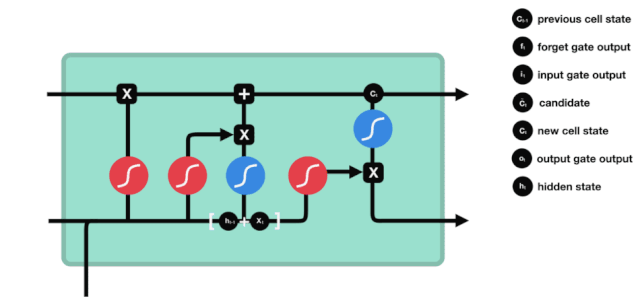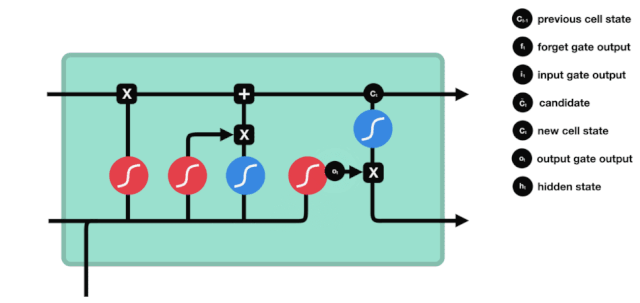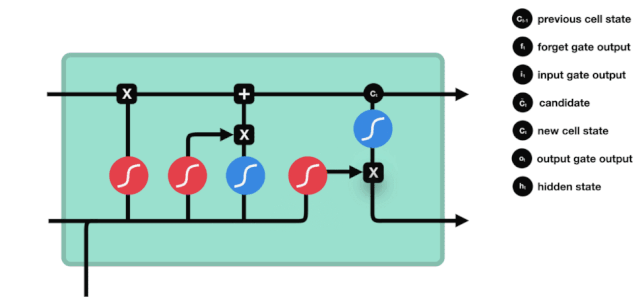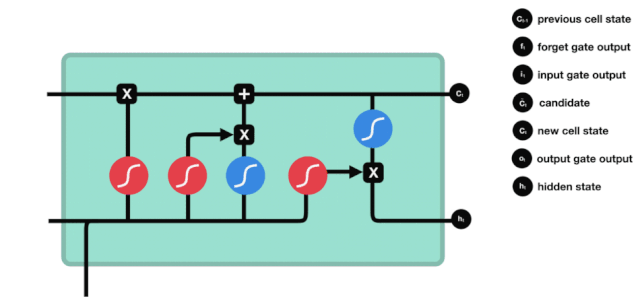
Chúng ta thấy thông tin $h_{l-1}$ và $x_{t}$ được thêm vào một cửa quên (sigmoid) và một cửa nhập (tanh). Vì đầu ra của cửa quên là 0-1, do đó, nếu cửa quên là 0, kết quả sau khi nhập $C_{i}$ sẽ không được thêm vào trạng thái tế bào hiện tại, nếu là 1, tất cả sẽ được thêm vào trạng thái tế bào, do đó, vai trò của cửa quên ở đây là chọn lọc kết quả của cửa nhập vào trạng thái tế bào.

Công thức toán học là: $C_{t}=f_{t} * C_{t-1} + i_{t} * \tilde{C}_{t} $

Cổng ra

Sau khi cập nhật trạng thái tế bào, các đặc điểm trạng thái của tế bào đầu ra cần được xác định dựa trên tổng của $h_{l-1}$ và $x_{t}$ được nhập vào, điều này đòi hỏi phải đưa vào qua một lớp sigmoid được gọi là cửa đầu ra để có được các điều kiện được xác định, sau đó đưa trạng thái tế bào qua lớp tanh để có được một vector có giá trị từ -1 đến 1, phương trình này được nhân với các điều kiện được xác định của cửa đầu ra để có được đầu ra của đơn vị RNA cuối cùng, hình ảnh động như sau:

def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

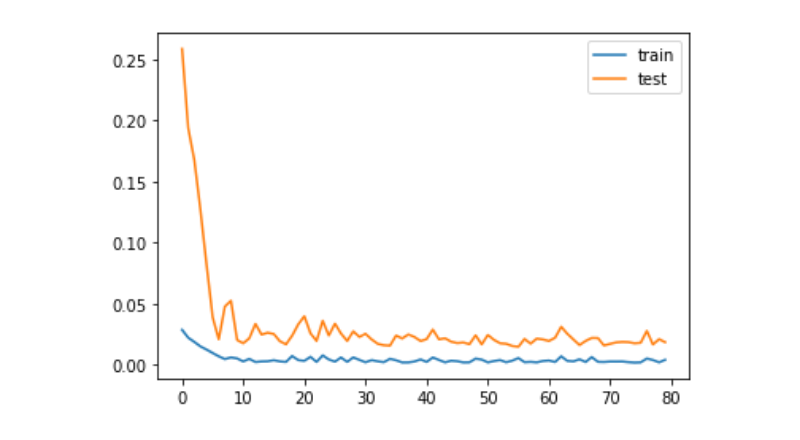
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Dự báo

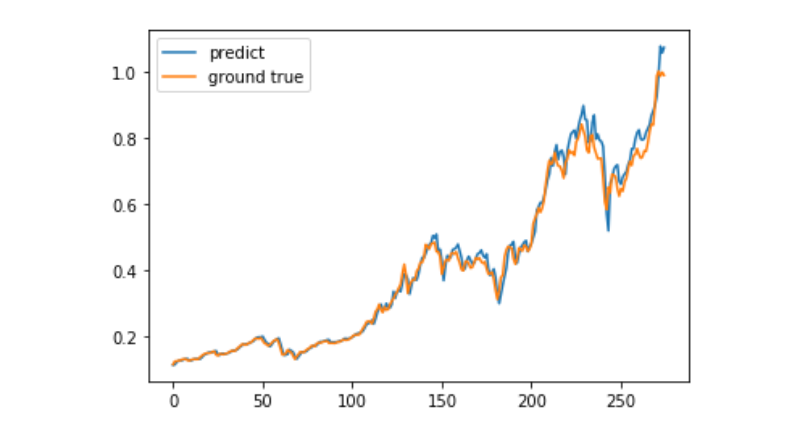
predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

Hiện tại, việc sử dụng máy học để dự đoán xu hướng giá Bitcoin trong thời gian dài là rất khó khăn, và bài viết này chỉ được sử dụng như một trường hợp học tập. Trường hợp này sẽ được đưa ra trực tuyến và trong hình ảnh demo của đám mây ma trận, người dùng quan tâm có thể trải nghiệm trực tiếp.