Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện Chuyện

Trong số trước, chúng tôi đã nói rằng khi Jacob Bernoulli qua đời, ông vẫn chưa xuất bản cuốn sách của mình về thuyết xác suất. Nhiệm vụ biên soạn bản thảo của ông đã được giao cho cháu trai của ông, Nicholas II Bernoulli (đó là thiên tài ban đầu). Sau khi hoàn thành di chúc của chú, Nicholas bắt đầu muốn nghiên cứu mức độ sai lệch của xác suất thực trong trường hợp đã xác định số lần quan sát. Ông Moivre (Abraham de Moivre) đã được dịch thành ông Moivre ở nhiều nơi, nhưng sau khi nhìn thấy hình ảnh của ông, tôi không ủng hộ cách dịch sau này. Đáng lẽ lời mời này có thể đạt được một bài hát được ca ngợi về thế giới sau này, nhưng ông Moivre đã từ chối. Và lý do ông từ chối là vì ông cảm thấy mình chưa có đủ sức mạnh.

• Bạch Dương. Sau đó, vua Louis XIV của Pháp đã ban hành một sắc lệnh tuyên bố người Tin Lành trong nước là công dân kém cỏi, trẻ em phải cải đạo sang Tin Lành, và điều này đã làm cho Tin Lành ở Pháp trở thành một giáo phái, và Tin Lành đã bị bỏ tù hai năm. Sau khi thoát khỏi tù, Tin Lành đã tìm cách chạy trốn sang Anh, nhưng ông đã không được giảng dạy trong giới học thuật, mặc dù ông là bạn của Newton và mặc dù ông là thành viên của gia đình hoàng gia Anh ở tuổi 30.

Nhưng chúng ta vẫn phải kêu lên ở đây, Dunmore sẽ không bao giờ chết! Năm 1711, Dunmore đã xuất bản một câu chuyện thần thoại về thước đo may mắn, và nếu có một cuốn sách được xuất bản vào thời điểm đó, nó chắc chắn sẽ có lời khuyên của Newton: Hãy hỏi ông Dunmore, ông ấy biết nhiều hơn tôi về điều này.

Không phải lúc đó, vì vậy, Don Moffat đã không có cơ hội kiếm được nhiều tiền từ bản quyền.

Bạn cũng nên nhớ câu hỏi mà chúng ta đã đề cập ở bài trước đó (tạm dịch: Câu chuyện nhỏ về mạo hiểm): Binh nhân Bernoulli, đối với 5000 viên đá trong một cái xô, chúng ta có thể thực hiện 25.500 lần thu thập để ước tính tỷ lệ của tổng số viên đá. Nhưng bạn cũng nên nhận ra rằng 25.500 lần thu thập lặp lại là quá nhiều, nó còn tốt hơn là đổ một viên đá ra một số.

Sử dụng phương pháp tính toán và hình tam giác Pascal, Dunmower đã lấy phương pháp lấy mẫu theo nhóm. Ông giả định rằng mỗi lần lấy 100 viên đá từ trong thùng, ghi lại tỷ lệ của viên đá đen và trắng, đặt lại và lấy lại. Bằng cách này, Dunmower có thể cho bạn biết trước sự lệch xấp xỉ của tỷ lệ bạn ghi lại với tỷ lệ thực và tỷ lệ này sẽ phân bố như thế nào xung quanh giá trị trung bình của chúng.

Câu nói này có giống như quen thuộc, hay là cảm giác ngay trên miệng, hay là ngay lập tức muốn gọi tên nó? Vâng, đây là sự phân phối chính xác mà tất cả chúng ta đều quen thuộc. Đường cong của sự phân phối chính xác giống như một đường cong hình chuông, hầu hết các giá trị quan sát tập trung ở giữa, gần với trung bình của tất cả các giá trị quan sát, sau đó từ trung bình nghiêng đối xứng về hai đầu, và số lượng quan sát ở hai đầu của trung bình là bằng nhau.

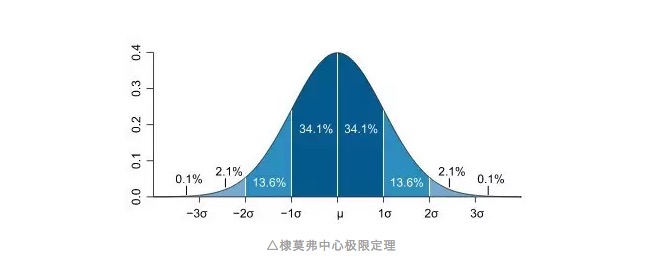
Như vậy chúng ta có thể giới thiệu khái niệm chênh lệch chuẩn, mà chúng ta đã đề cập đến nó trong các bài viết khác của số công chúng tại sao chênh lệch chuẩn? đo lường rủi ro trong mắt của Thượng đế. Sự chênh lệch chuẩn thực sự mô tả mức độ lệch của giá trị quan sát so với giá trị trung bình, hoặc chúng ta hiểu nó như là đơn vị lệch so với giá trị trung bình. Đối với một phân phối chính xác, tỷ lệ của 100 khối đá bạch cầu chúng ta lấy ra, khoảng 68% sẽ nằm trong phạm vi chênh lệch chuẩn hai bên của giá trị trung bình, trong khi phạm vi chênh lệch hai tiêu chuẩn có thể bao gồm khoảng 95% giá trị quan sát.

Là một tín đồ đạo đức, Dunmore cho rằng đường cong hình chuông là sản phẩm của Thiên Chúa. Theo ông, bằng cách đo lường như vậy, chúng ta có thể chiến thắng sự không chắc chắn và sau đó chinh phục tất cả các rủi ro, bởi vì đường cong đã mô tả tất cả các hiện tượng có thể xảy ra và xác suất của chúng, có lẽ do sự ngẫu nhiên sẽ tạo ra cái gọi là lệch lạc, nhưng theo thời gian, những lệch lạc này sẽ không ảnh hưởng đến quy luật mà chúng ta tổng hợp.

Theo cách giải thích của mọi người, điều mà Tom Morver nói là Tom thất vọng là đôi khi không thể gọi được số điện thoại, cố gắng nhiều lần và luôn trả lời Tom. Ở trường trung học còn có một bài học cổ điển ((Ôi, tại sao tôi luôn sử dụng bài học trung học)) là về tỷ lệ vượt qua sản phẩm. Nếu đối với một loạt sản phẩm, tiêu chuẩn ngành công nghiệp cho rằng tỷ lệ chất thải không quá 0,1% là đủ tiêu chuẩn, điều này có nghĩa là chúng ta chọn 10.000 sản phẩm một cách ngẫu nhiên, trong đó nếu chất thải không quá 10, sẽ được vượt qua.

Tuy nhiên, trong hầu hết các trường hợp, câu hỏi này không có ý nghĩa gì với chúng ta. Bởi vì thực tế chúng ta có thể không biết tỷ lệ chất thải trung bình của sản phẩm là bao nhiêu, và nếu tỷ lệ chất thải trung bình cao hơn tiêu chuẩn kiểm tra, thì một loạt sản phẩm của chúng ta có khả năng vượt qua kiểm tra như thế nào? Nếu lấy 20.000 sản phẩm để kiểm tra, thì kết quả của 10.000 sản phẩm có thể được sử dụng trực tiếp không?

Tóm tắt từ Trung Quốc Quantified Investment Society