Một công cụ mạnh mẽ cho các nhà giao dịch theo chương trình: thuật toán cập nhật gia tăng để tính toán trung bình và biến thể

Lời giới thiệu

Trong giao dịch theo chương trình, thường cần phải tính toán trung bình và biến thể, chẳng hạn như tính toán trung bình động và chỉ số biến động. Khi chúng ta cần tính toán tần suất cao và dài hạn, cần phải giữ dữ liệu lịch sử trong một thời gian dài, điều này là không cần thiết và tốn nhiều tài nguyên. Bài viết này giới thiệu một thuật toán cập nhật trực tuyến để tính toán trung bình và biến thể, đặc biệt quan trọng cho việc xử lý luồng dữ liệu thời gian thực và điều chỉnh năng động các chiến lược giao dịch, đặc biệt là các chiến lược tần suất cao. Bài viết cũng cung cấp việc thực hiện mã Python tương ứng để giúp các nhà giao dịch nhanh chóng triển khai và áp dụng thuật toán trong giao dịch thực tế.

Trung bình đơn giản và biến thể

Nếu chúng ta dùng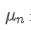để đại diện cho giá trị trung bình của điểm dữ liệu số n, giả sử rằng chúng ta đã tính trung bình của n-1 điểm dữ liệu /upload/asset/28e28ae0beba5e8a810a6.png, bây giờ chúng ta nhận được một điểm dữ liệu mới /upload/asset/28d4723cf4cab1cf78f50.png. Chúng ta muốn tính số trung bình mới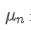Sau đây là một dẫn xuất chi tiết.

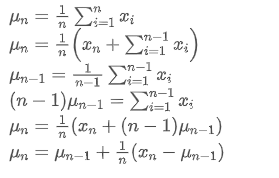
Quá trình cập nhật biến thể có thể được chia thành các bước sau:

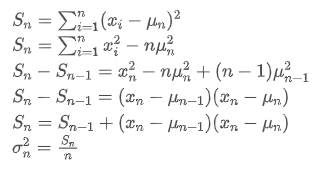
Như có thể thấy từ hai công thức trên, quá trình này cho phép chúng ta cập nhật trung bình và biến thể mới khi nhận được mỗi điểm dữ liệu mới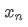bằng cách duy trì chỉ trung bình và biến thể của dữ liệu trước đó, mà không lưu dữ liệu lịch sử, làm cho tính toán hiệu quả hơn. Tuy nhiên, vấn đề là những gì chúng ta tính toán theo cách này là trung bình và biến thể của tất cả các mẫu, trong khi trong các chiến lược thực tế, chúng ta cần xem xét một khoảng thời gian cố định nhất định. Quan sát cập nhật trung bình trên cho thấy số lượng cập nhật trung bình mới là độ lệch giữa dữ liệu mới và trung bình trước đây nhân với một tỷ lệ. Nếu tỷ lệ này được cố định, nó sẽ dẫn đến một trung bình trọng số theo cấp số nhân, mà chúng ta sẽ thảo luận tiếp theo.

Trung bình trọng số theo hàm số nhân

Mức trung bình trọng số nhân có thể được xác định bằng mối quan hệ tái diễn sau:

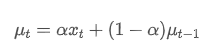
Trong số đó,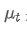là trung bình trọng số nhân tại thời điểm t,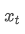là giá trị được quan sát tại thời điểm t, α là yếu tố trọng lượng, và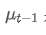là chỉ số trung bình trọng số của thời điểm trước đó.

Phân biến được cân nhắc theo hàm số nhân

Đối với biến thể, chúng ta cần tính toán trung bình trọng số nhân của các độ lệch bình phương tại mỗi thời điểm.

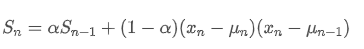
Trong số đó,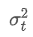là biến thể trọng số nhân tại thời điểm t, và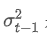là biến thể cân nhắc theo hàm số của thời điểm trước.

Quan sát trung bình và biến thể trọng số theo hàm số nhân, các cập nhật gia tăng của chúng là trực quan, giữ lại một phần các giá trị trong quá khứ và thêm các thay đổi mới.https://fanf2.user.srcf.net/hermes/doc/antiforgery/stats.pdf

SMA và EMA

SMA (còn được gọi là trung bình số học) và EMA là hai biện pháp thống kê phổ biến, mỗi biện pháp có các đặc điểm và cách sử dụng khác nhau. Đệ nhất gán trọng lượng bằng nhau cho mỗi quan sát, phản ánh vị trí trung tâm của tập dữ liệu.

• Phân phối trọng lượng: SMA gán cùng trọng lượng cho mỗi điểm dữ liệu, trong khi EMA gán trọng lượng cao hơn cho các điểm dữ liệu gần đây nhất.
• Nhạy cảm với thông tin mới: SMA không đủ nhạy cảm với dữ liệu mới được thêm vào, vì nó liên quan đến việc tính lại tất cả các điểm dữ liệu.
• Sự phức tạp tính toán: Việc tính toán SMA tương đối đơn giản, nhưng khi số điểm dữ liệu tăng lên, chi phí tính toán cũng tăng lên.

Phương pháp chuyển đổi gần đúng giữa EMA và SMA

Mặc dù SMA và EMA khác nhau về khái niệm, chúng ta có thể làm cho EMA gần gũi với SMA có chứa một số lượng quan sát cụ thể bằng cách chọn một giá trị α thích hợp. Mối quan hệ gần gũi này có thể được mô tả bằng kích thước mẫu hiệu quả, đó là hàm của yếu tố trọng lượng α trong EMA.

SMA là trung bình số học của tất cả các giá trong một cửa sổ thời gian nhất định. Đối với một cửa sổ thời gian N, trung tâm của SMA (tức là vị trí mà số trung bình nằm) có thể được coi là:

trung tâm của SMA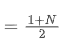

EMA là một loại trung bình trọng số mà các điểm dữ liệu gần đây nhất có trọng lượng lớn hơn.

trung tâm của EMA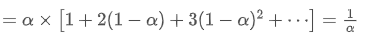

Khi chúng ta giả định rằng SMA và EMA có cùng một trung tâm, chúng ta có thể nhận được:

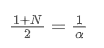
Để giải phương trình này, chúng ta có thể lấy mối quan hệ giữa α và N.

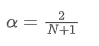
Điều này có nghĩa là đối với một SMA N ngày nhất định, giá trị α tương ứng có thể được sử dụng để tính toán EMA tương đương, để chúng có cùng một trung tâm và kết quả rất giống nhau.

Chuyển đổi EMA với tần số cập nhật khác nhau

Giả sử chúng ta có một EMA cập nhật mỗi giây, với một yếu tố trọng lượng là /upload/asset/28da19ef219cae323a32f.png. Điều này có nghĩa là mỗi giây, điểm dữ liệu mới sẽ được thêm vào EMA với trọng lượng là /upload/asset/28da19ef219cae323a32f.png, trong khi ảnh hưởng của các điểm dữ liệu cũ sẽ được nhân với /upload/asset/28cfb008ac438a12e1127.png.

Nếu chúng ta thay đổi tần suất cập nhật, chẳng hạn như cập nhật mỗi f giây một lần, chúng ta muốn tìm một yếu tố trọng lượng mới /upload/asset/28d2d28762e349a03c531.png, để tác động tổng thể của các điểm dữ liệu trong f giây là giống như khi cập nhật mỗi giây.

Trong vòng f giây, nếu không thực hiện cập nhật, tác động của các điểm dữ liệu cũ sẽ liên tục suy giảm f lần, mỗi lần nhân /upload/asset/28e50eb9c37d5626d6691.png. Do đó, tổng nhân phân rã sau f giây là /upload/asset/28e296f97d8c8344a2ee6.png.

Để làm cho EMA được cập nhật mỗi f giây có hiệu ứng phân rã tương tự như EMA được cập nhật mỗi giây trong một khoảng thời gian cập nhật, chúng tôi đặt tổng nhân tố phân rã sau f giây bằng nhân tố phân rã trong một khoảng thời gian cập nhật:

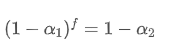
Giải quyết phương trình này, chúng ta có được các yếu tố trọng lượng mới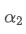

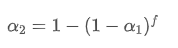
Công thức này cung cấp giá trị ước tính của yếu tố trọng lượng mới /upload/asset/28d2d28762e349a03c531.png, giữ hiệu ứng làm mịn EMA không thay đổi khi tần suất cập nhật thay đổi. Ví dụ: Khi chúng ta tính giá trung bình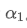với một giá trị 0,001 và cập nhật nó mỗi 10 giây, nếu nó được thay đổi để cập nhật mỗi giây, giá trị tương đương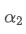sẽ khoảng 0,01.

Thực hiện mã Python

class ExponentialWeightedStats:
    def __init__(self, alpha):
        self.alpha = alpha
        self.mu = 0
        self.S = 0
        self.initialized = False

    def update(self, x):
        if not self.initialized:
            self.mu = x
            self.S = 0
            self.initialized = True
        else:
            temp = x - self.mu
            new_mu = self.mu + self.alpha * temp
            self.S = self.alpha * self.S + (1 - self.alpha) * temp * (x - self.mu)
            self.mu = new_mu

    @property
    def mean(self):
        return self.mu

    @property
    def variance(self):
        return self.S

# Usage example
alpha = 0.05  # Weight factor
stats = ExponentialWeightedStats(alpha)
data_stream = [] # Data stream
for data_point in data_stream:
    stats.update(data_point)

Tóm lại

Trong giao dịch theo chương trình tần số cao, việc xử lý dữ liệu nhanh chóng trong thời gian thực là rất quan trọng. Để cải thiện hiệu quả tính toán và giảm tiêu thụ tài nguyên, bài viết này giới thiệu một thuật toán cập nhật trực tuyến để tính toán liên tục trung bình trọng số và biến thể của một luồng dữ liệu. Các bản cập nhật gia tăng thời gian thực cũng có thể được sử dụng cho các tính toán dữ liệu thống kê và chỉ số khác nhau, chẳng hạn như mối tương quan giữa hai giá tài sản, phù hợp tuyến tính, vv, với tiềm năng lớn. Việc cập nhật gia tăng coi dữ liệu như một hệ thống tín hiệu, đó là sự tiến hóa trong suy nghĩ so với tính toán định kỳ. Nếu chiến lược của bạn vẫn bao gồm các phần tính toán bằng cách sử dụng dữ liệu lịch sử, hãy xem xét chuyển đổi nó theo cách tiếp cận này: chỉ ghi lại ước tính tình trạng hệ thống và cập nhật tình trạng hệ thống khi dữ liệu mới đến; lặp lại chu kỳ này tiếp theo.