Giao dịch cặp dựa trên công nghệ dữ liệu

Giao dịch cặp dựa trên công nghệ dữ liệu

Giao dịch cặp là một ví dụ tốt về việc xây dựng các chiến lược giao dịch dựa trên phân tích toán học.

Nguyên tắc cơ bản

Giả sử bạn có một cặp mục tiêu đầu tư X và Y có một số kết nối tiềm năng. Ví dụ, hai công ty sản xuất cùng một sản phẩm, chẳng hạn như Pepsi Cola và Coca Cola. Bạn muốn tỷ lệ giá hoặc chênh lệch cơ bản (còn được gọi là chênh lệch giá) của hai sản phẩm này không thay đổi theo thời gian. Tuy nhiên, do những thay đổi tạm thời trong cung và nhu cầu, chẳng hạn như một đơn đặt hàng mua / bán lớn của mục tiêu đầu tư, và phản ứng với tin tức quan trọng của một trong các công ty, sự khác biệt giá giữa hai cặp có thể khác nhau theo thời gian. Trong trường hợp này, một đối tượng đầu tư di chuyển lên trong khi đối tượng khác di chuyển xuống tương đối với nhau. Nếu bạn muốn sự bất đồng này trở lại bình thường theo thời gian, bạn có thể tìm thấy các cơ hội giao dịch (hoặc cơ hội điều chỉnh).

Khi có sự khác biệt giá tạm thời, bạn sẽ bán đối tượng đầu tư có hiệu suất tuyệt vời ( đối tượng đầu tư tăng) và mua đối tượng đầu tư có hiệu suất kém ( đối tượng đầu tư giảm). Bạn chắc chắn rằng lợi nhuận giữa hai đối tượng đầu tư cuối cùng sẽ giảm thông qua sự sụt giảm của đối tượng đầu tư có hiệu suất tuyệt vời hoặc sự gia tăng của đối tượng đầu tư có hiệu suất kém, hoặc cả hai. Giao dịch của bạn sẽ kiếm tiền trong tất cả các tình huống tương tự này. Nếu các đối tượng đầu tư di chuyển lên hoặc xuống cùng nhau mà không thay đổi sự khác biệt giá giữa chúng, bạn sẽ không kiếm được hoặc mất tiền.

Do đó, giao dịch cặp là một chiến lược giao dịch trung lập thị trường, cho phép các nhà giao dịch kiếm lợi từ hầu hết các điều kiện thị trường: xu hướng tăng, xu hướng giảm hoặc hợp nhất theo chiều ngang.

Giải thích khái niệm: hai mục tiêu đầu tư giả định

• Xây dựng môi trường nghiên cứu trên nền tảng FMZ Quant

Trước hết, để làm việc trơn tru, chúng ta cần xây dựng môi trường nghiên cứu của mình.FMZ.COM) để xây dựng môi trường nghiên cứu của chúng tôi, chủ yếu để sử dụng giao diện API thuận tiện và nhanh chóng và hệ thống Docker được đóng gói tốt của nền tảng này sau đó.

Trong tên chính thức của nền tảng FMZ Quant, hệ thống Docker này được gọi là hệ thống Docker.

Vui lòng tham khảo bài viết trước của tôi về cách triển khai một docker và robot:https://www.fmz.com/bbs-topic/9864.

Người đọc muốn mua máy chủ điện toán đám mây của riêng mình để triển khai các dockers có thể tham khảo bài viết này:https://www.fmz.com/digest-topic/5711.

Sau khi triển khai thành công máy chủ điện toán đám mây và hệ thống docker, tiếp theo chúng tôi sẽ cài đặt hiện tại lớn nhất hiện vật của Python: Anaconda

Để thực hiện tất cả các môi trường chương trình có liên quan (thư viện phụ thuộc, quản lý phiên bản, v.v.) được yêu cầu trong bài viết này, cách đơn giản nhất là sử dụng Anaconda.

Đối với phương pháp cài đặt của Anaconda, vui lòng tham khảo hướng dẫn chính thức của Anaconda:https://www.anaconda.com/distribution/.

Bài viết này cũng sẽ sử dụng numpy và panda, hai thư viện phổ biến và quan trọng trong máy tính khoa học Python.

Công trình cơ bản trên cũng có thể tham chiếu đến các bài viết trước của tôi, giới thiệu cách thiết lập môi trường Anaconda và thư viện numpy và panda.https://www.fmz.com/bbs-topic/9863.

Tiếp theo, hãy sử dụng mã để thực hiện một mục tiêu đầu tư giả định:

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Vâng, chúng ta cũng sẽ sử dụng matplotlib, một thư viện biểu đồ rất nổi tiếng trong Python.

Hãy tạo ra một mục tiêu đầu tư giả định X, và mô phỏng và vẽ lãi suất hàng ngày của nó thông qua phân bố bình thường.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

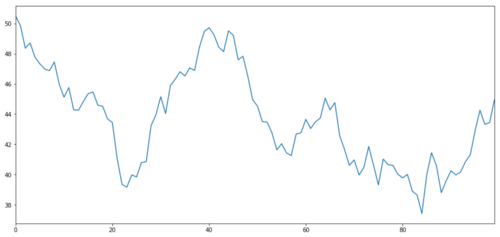
X của đối tượng đầu tư được mô phỏng để vẽ lợi nhuận hàng ngày của nó thông qua một phân bố bình thường

Bây giờ chúng ta tạo ra Y, được tích hợp mạnh mẽ với X, vì vậy giá của Y nên rất giống với sự thay đổi của X. Chúng ta mô hình hóa điều này bằng cách lấy X, di chuyển nó lên và thêm một số tiếng ồn ngẫu nhiên chiết xuất từ phân bố bình thường.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

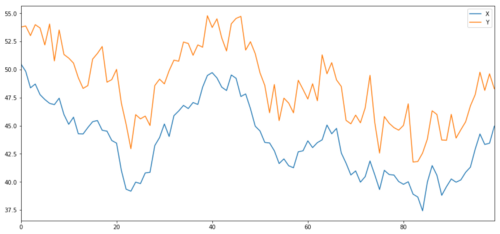
X và Y của đối tượng đầu tư hợp nhất

Tích hợp

Tích hợp rất giống với tương quan, có nghĩa là tỷ lệ giữa hai chuỗi dữ liệu sẽ thay đổi gần giá trị trung bình.

Y = X + e

Nơi là một tỷ lệ không đổi và e là tiếng ồn.

Đối với các cặp giao dịch giữa hai chuỗi thời gian, giá trị dự kiến của tỷ lệ theo thời gian phải hội tụ với giá trị trung bình, nghĩa là chúng nên được tích hợp.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

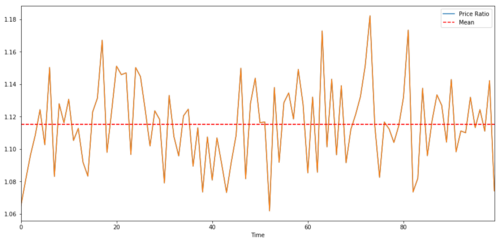
Tỷ lệ và giá trị trung bình giữa hai giá mục tiêu đầu tư tích hợp

Xét nghiệm hợp nhất

Một phương pháp kiểm tra thuận tiện là sử dụng statsmodels.tsa.stattools. Chúng ta sẽ thấy một giá trị p rất thấp, bởi vì chúng ta đã tạo ra hai chuỗi dữ liệu nhân tạo được tích hợp hợp nhất có thể.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Kết quả là: 1.81864477307e-17

Lưu ý: tương quan và hợp nhất

Tương quan và hợp nhất, mặc dù tương tự nhau về lý thuyết, nhưng không giống nhau. Hãy xem các ví dụ về các chuỗi dữ liệu có liên quan nhưng không hợp nhất và ngược lại.

X.corr(Y)

Kết quả là: 0,951

Một ví dụ đơn giản là một chuỗi của hai dữ liệu lệch.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

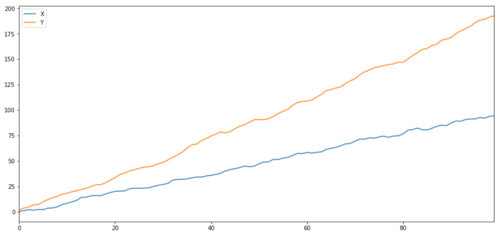
Hai loạt liên quan (không tích hợp với nhau)

Tỷ lệ tương quan: 0,998 Giá trị P của thử nghiệm hợp nhất: 0,258

Các ví dụ đơn giản về hợp nhất mà không có mối tương quan là chuỗi phân phối bình thường và sóng vuông.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()
Y3[0:100] = 30

Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

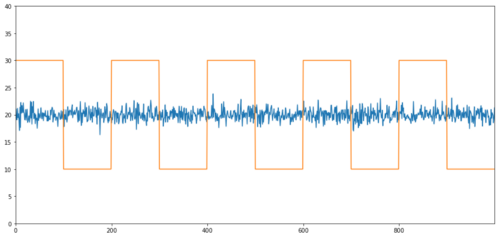
Sự tương quan: 0,007546 Giá trị P của thử nghiệm hợp nhất: 0.0

Sự tương quan rất thấp, nhưng giá trị p cho thấy sự tích hợp hoàn hảo!

Làm thế nào để tiến hành giao dịch cặp?

Do hai chuỗi thời gian tích hợp (như X và Y ở trên) đối diện nhau và lệch nhau, đôi khi mức chênh lệch cơ sở cao hoặc thấp. Chúng tôi thực hiện giao dịch cặp bằng cách mua một đối tượng đầu tư và bán một đối tượng khác. Bằng cách này, nếu hai mục tiêu đầu tư giảm hoặc tăng cùng nhau, chúng tôi sẽ không kiếm tiền hoặc mất tiền, nghĩa là chúng tôi trung lập trên thị trường.

Trở lại như trên, X và Y trong Y = X + e, để tỷ lệ (Y / X) di chuyển xung quanh giá trị trung bình của nó . Chúng tôi kiếm tiền thông qua tỷ lệ đảo ngược giá trị trung bình. Để làm điều này, chúng tôi sẽ chú ý đến trường hợp X và Y cách xa nhau, tức là giá trị của quá cao hoặc quá thấp:

• Đi dài tỷ lệ: Đây là khi tỷ lệ rất nhỏ và chúng tôi mong đợi nó sẽ tăng.

• Tỷ lệ đi ngắn: Đây là khi tỷ lệ rất lớn và chúng tôi mong đợi nó sẽ giảm.

Vui lòng lưu ý rằng chúng tôi luôn có một vị trí bảo hiểm: nếu chủ thể giao dịch mua giá trị lỗ, vị trí mua sẽ kiếm tiền, và ngược lại, vì vậy chúng tôi miễn dịch với xu hướng thị trường tổng thể.

Nếu X và Y của đối tượng giao dịch di chuyển tương đối với nhau, chúng ta sẽ kiếm tiền hoặc mất tiền.

Sử dụng dữ liệu để tìm các đối tượng giao dịch có hành vi tương tự

Cách tốt nhất để làm điều này là bắt đầu từ đối tượng giao dịch mà bạn nghi ngờ có thể là hợp nhất và thực hiện một bài kiểm tra thống kê.khuynh hướng so sánh nhiều lần.

Sự thiên vị so sánh nhiều lầnđề cập đến khả năng tăng của việc tạo ra các giá trị p quan trọng không chính xác khi chạy nhiều bài kiểm tra, bởi vì chúng ta cần chạy một số lượng lớn các bài kiểm tra. Nếu chúng ta chạy 100 bài kiểm tra trên dữ liệu ngẫu nhiên, chúng ta nên thấy 5 giá trị p dưới 0,05. Nếu bạn muốn so sánh n mục tiêu giao dịch cho hợp nhất, bạn sẽ thực hiện n (n-1) / 2 so sánh, và bạn sẽ thấy nhiều giá trị p không chính xác, sẽ tăng lên với sự gia tăng các mẫu thử nghiệm của bạn. Để tránh tình huống này, hãy chọn một vài cặp giao dịch và bạn có lý do để xác định rằng chúng có thể là hợp nhất, và sau đó kiểm tra chúng riêng biệt. Điều này sẽ làm giảm đáng kểkhuynh hướng so sánh nhiều lần.

Vì vậy, hãy thử tìm một số mục tiêu giao dịch cho thấy sự tích hợp. Hãy lấy một giỏ cổ phiếu công nghệ lớn của Mỹ trong chỉ số S&P 500 làm ví dụ. Những mục tiêu giao dịch này hoạt động trong các phân khúc thị trường tương tự và có giá tích hợp. Chúng tôi quét danh sách các đối tượng giao dịch và kiểm tra sự tích hợp giữa tất cả các cặp.

Ma trận điểm thử nghiệm hợp nhất được trả lại, ma trận giá trị p và tất cả các cặp có giá trị p nhỏ hơn 0,05.Phương pháp này dễ bị thiên vị so sánh nhiều lần, vì vậy trên thực tế, họ cần thực hiện xác minh thứ hai.Trong bài viết này, để dễ dàng giải thích, chúng tôi chọn bỏ qua điểm này trong ví dụ.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Lưu ý: Chúng tôi đã bao gồm điểm chuẩn thị trường (SPX) trong dữ liệu - thị trường đã thúc đẩy dòng chảy của nhiều đối tượng giao dịch. Thông thường bạn có thể tìm thấy hai đối tượng giao dịch dường như được tích hợp; Nhưng trên thực tế, chúng không tích hợp với nhau, nhưng với thị trường. Điều này được gọi là biến gây nhầm lẫn. Điều quan trọng là kiểm tra sự tham gia thị trường trong bất kỳ mối quan hệ nào bạn tìm thấy.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Bây giờ hãy thử sử dụng phương pháp của chúng tôi để tìm các cặp giao dịch tích hợp.

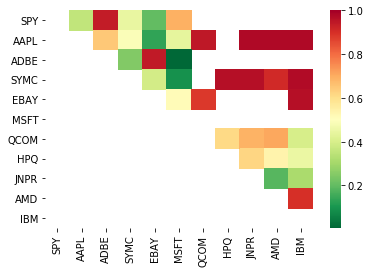
# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

ADBE và MSFT được tích hợp với nhau.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

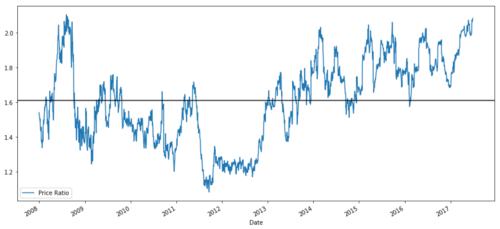
Biểu đồ tỷ lệ giá giữa MSFT và ADBE từ năm 2008 đến 2017

Tỷ lệ này trông giống như một mức trung bình ổn định. Tỷ lệ tuyệt đối không hữu ích về mặt thống kê. Nó hữu ích hơn để tiêu chuẩn hóa tín hiệu của chúng ta bằng cách xử lý chúng như Điểm Z. Điểm Z được định nghĩa là:

Điểm số Z (giá trị) = (giá trị trung bình) / Sai lệch chuẩn

Cảnh báo

Trong thực tế, chúng ta thường cố gắng mở rộng dữ liệu dựa trên giả định rằng dữ liệu được phân bố bình thường. Tuy nhiên, nhiều dữ liệu tài chính không được phân bố bình thường, vì vậy chúng ta phải rất cẩn thận không đơn giản giả định bình thường hoặc bất kỳ phân bố cụ thể nào khi tạo số liệu thống kê. Sự phân bố thực sự của tỷ lệ có thể có hiệu ứng đuôi béo, và những dữ liệu có xu hướng cực đoan sẽ gây nhầm lẫn cho mô hình của chúng ta và dẫn đến tổn thất lớn.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

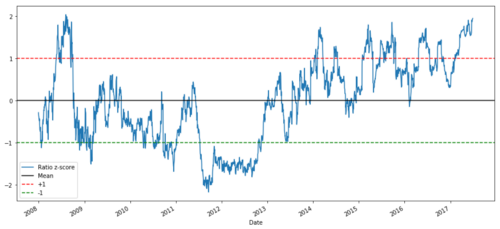
Tỷ lệ giá Z giữa MSFT và ADBE từ năm 2008 đến 2017

Bây giờ nó dễ dàng hơn để quan sát sự chuyển động của tỷ lệ gần giá trị trung bình, nhưng đôi khi nó dễ dàng để có một sự khác biệt lớn từ giá trị trung bình.

Bây giờ chúng ta đã thảo luận về kiến thức cơ bản về chiến lược giao dịch cặp, và xác định chủ đề tích hợp chung dựa trên giá lịch sử, hãy thử phát triển tín hiệu giao dịch.

• Thu thập dữ liệu đáng tin cậy và dọn dẹp dữ liệu;

• Tạo các chức năng từ dữ liệu để xác định tín hiệu giao dịch / logic;

• Các hàm có thể là các đường trung bình động hoặc dữ liệu giá, mối tương quan hoặc tỷ lệ của các tín hiệu phức tạp hơn - kết hợp chúng để tạo ra các hàm mới;

• Sử dụng các chức năng này để tạo ra tín hiệu giao dịch, tức là tín hiệu mua, bán hoặc vị trí ngắn để theo dõi.

May mắn thay, chúng ta có nền tảng FMZ Quant (fmz.com), đã hoàn thành bốn khía cạnh trên cho chúng tôi, đó là một ân phước lớn cho các nhà phát triển chiến lược.

Trong nền tảng FMZ Quant, có các giao diện được đóng gói cho các giao dịch chính khác nhau. Những gì chúng ta cần làm là gọi các giao diện API này. Phần còn lại của logic thực hiện cơ bản đã được hoàn thành bởi một nhóm chuyên nghiệp.

Để hoàn thành logic và giải thích nguyên tắc trong bài viết này, chúng tôi sẽ trình bày chi tiết về logic cơ bản này. Tuy nhiên, trong hoạt động thực tế, người đọc có thể gọi giao diện FMZ Quant API trực tiếp để hoàn thành bốn khía cạnh trên.

Hãy bắt đầu:

Bước 1: Đặt câu hỏi

Ở đây, chúng ta cố gắng tạo ra một tín hiệu để cho chúng ta biết liệu tỷ lệ sẽ mua hoặc bán tại thời điểm tiếp theo, đó là biến dự đoán của chúng tôi Y:

Y = Tỷ lệ là mua (1) hoặc bán (-1)

Y ((t) = Sign ((Ratio ((t+1) Ratio ((t))

Xin lưu ý rằng chúng tôi không cần dự đoán giá mục tiêu giao dịch thực tế, hoặc thậm chí là giá trị thực tế của tỷ lệ (mặc dù chúng tôi có thể), nhưng chỉ hướng tỷ lệ trong bước tiếp theo.

Bước 2: Thu thập dữ liệu đáng tin cậy và chính xác

FMZ Quant là bạn của bạn! Bạn chỉ cần chỉ định đối tượng giao dịch được giao dịch và nguồn dữ liệu được sử dụng, và nó sẽ trích xuất dữ liệu cần thiết và xóa nó cho phân chia cổ tức và đối tượng giao dịch. Vì vậy, dữ liệu ở đây rất sạch sẽ.

Trong các ngày giao dịch trong 10 năm qua (khoảng 2500 điểm dữ liệu), chúng tôi đã thu thập các dữ liệu sau đây bằng cách sử dụng Yahoo Finance: giá mở cửa, giá đóng cửa, giá cao nhất, giá thấp nhất và khối lượng giao dịch.

Bước 3: Phân chia dữ liệu

Đừng quên bước rất quan trọng này trong việc kiểm tra độ chính xác của mô hình.

• Đào tạo 7 năm ~ 70%

• Thử nghiệm ~ 3 năm 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

Lý tưởng nhất, chúng ta cũng nên tạo ra các bộ xác nhận, nhưng chúng ta sẽ không làm điều đó ngay bây giờ.

Bước 4: Kỹ thuật tính năng

Chúng ta muốn dự đoán hướng thay đổi tỷ lệ. Chúng ta đã thấy rằng hai mục tiêu giao dịch của chúng ta được tích hợp lại, vì vậy tỷ lệ này có xu hướng thay đổi và trở lại giá trị trung bình. Có vẻ như các đặc điểm của chúng ta nên là một số biện pháp của tỷ lệ trung bình, và sự khác biệt giữa giá trị hiện tại và giá trị trung bình có thể tạo ra tín hiệu giao dịch của chúng ta.

Chúng tôi sử dụng các hàm sau:

• Tỷ lệ trung bình động 60 ngày: đo lường trung bình lăn;

• Tỷ lệ trung bình động 5 ngày: đo giá trị hiện tại của trung bình;

• 60 ngày lệch chuẩn;

• Điểm số Z: (5d MA - 60d MA) / 60d SD.

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

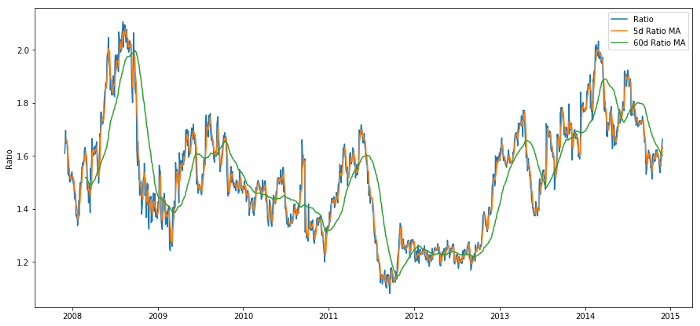
Tỷ lệ giá giữa 60d và 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

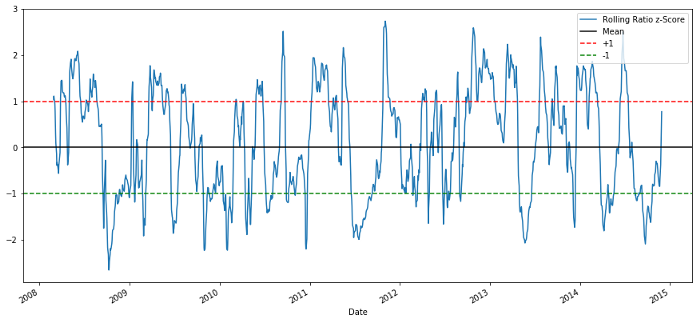
60-5 Z tỷ lệ giá điểm

Điểm số Z của giá trị trung bình lăn không đưa ra các thuộc tính hồi quy giá trị trung bình của tỷ lệ!

Bước 5: Chọn mô hình

Hãy bắt đầu với một mô hình rất đơn giản. Nhìn vào biểu đồ điểm số z, chúng ta có thể thấy rằng nếu điểm số z quá cao hoặc quá thấp, nó sẽ trở lại.

• Khi z dưới -1.0, tỷ lệ là mua (1), bởi vì chúng ta mong đợi z trở lại 0, vì vậy tỷ lệ tăng;

• Khi z trên 1,0, tỷ lệ là bán (- 1), bởi vì chúng ta mong đợi z trở lại 0, vì vậy tỷ lệ giảm.

Bước 6: Đào tạo, xác minh và tối ưu hóa

Cuối cùng, hãy xem xét tác động thực tế của mô hình của chúng tôi đối với dữ liệu thực tế.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

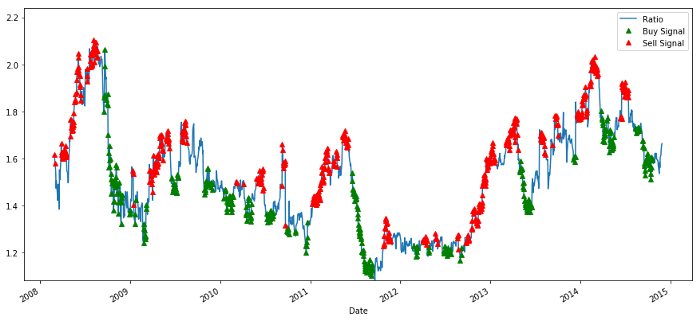
Tín hiệu tỷ lệ giá mua và bán

Dấu hiệu dường như hợp lý. Chúng ta dường như bán khi nó cao hoặc tăng (điểm đỏ) và mua lại khi nó thấp (điểm xanh) và giảm. Điều này có nghĩa là gì đối với đối tượng thực tế của giao dịch của chúng tôi? Hãy xem:

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

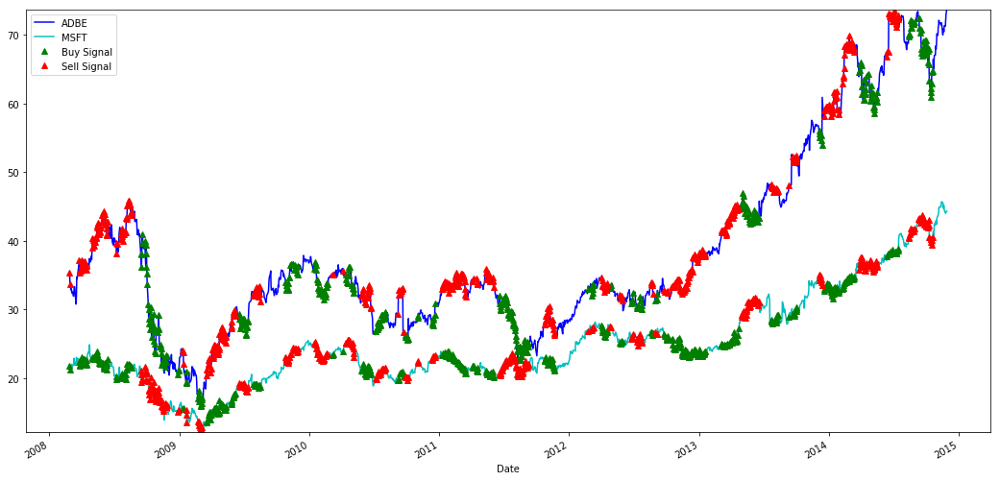
Các tín hiệu mua và bán cổ phiếu MSFT và ADBE

Xin hãy chú ý đến cách chúng tôi đôi khi kiếm lợi nhuận trên "chân ngắn", đôi khi trên "chân dài", và đôi khi cả hai.

Chúng tôi hài lòng với tín hiệu của dữ liệu đào tạo. Hãy xem tín hiệu này có thể tạo ra lợi nhuận như thế nào. Khi tỷ lệ thấp, chúng ta có thể thực hiện một kiểm tra trở lại đơn giản, mua tỷ lệ (mua 1 cổ phiếu ADBE và bán tỷ lệ x cổ phiếu MSFT), và bán tỷ lệ (bán 1 cổ phiếu ADBE và mua x tỷ lệ cổ phiếu MSFT) khi nó cao, và tính toán các giao dịch PnL của các tỷ lệ này.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Kết quả là: 1783.375

Bây giờ, chúng ta có thể tối ưu hóa hơn nữa bằng cách thay đổi cửa sổ thời gian trung bình động, bằng cách thay đổi ngưỡng mua / bán và đóng các vị trí, và kiểm tra cải thiện hiệu suất của dữ liệu xác thực.

Chúng ta cũng có thể thử các mô hình phức tạp hơn, chẳng hạn như Logistic regression và SVM, để dự đoán 1/-1.

Bây giờ, hãy tiến bộ mô hình này, dẫn chúng ta đến:

Bước 7: Kiểm tra lại dữ liệu thử nghiệm

Ở đây một lần nữa, nền tảng FMZ Quant áp dụng một công cụ backtesting QPS / TPS hiệu suất cao để tái tạo môi trường lịch sử một cách thực sự, loại bỏ những cạm bẫy backtesting định lượng phổ biến và phát hiện ra những thiếu sót của các chiến lược kịp thời, để giúp đỡ tốt hơn cho đầu tư bot thực sự.

Để giải thích nguyên tắc, bài viết này vẫn chọn để hiển thị logic cơ bản. Trong ứng dụng thực tế, chúng tôi khuyên độc giả sử dụng nền tảng FMZ Quant. Ngoài việc tiết kiệm thời gian, điều quan trọng là cải thiện tỷ lệ dung nạp lỗi.

Việc backtesting rất đơn giản. Chúng ta có thể sử dụng hàm trên để xem PnL của dữ liệu thử nghiệm.

trade(data['ADBE'].iloc[1762:], data['MSFT'].iloc[1762:], 60, 5)

Kết quả là: 5262.868

Mô hình đã làm một công việc tuyệt vời! Nó trở thành mô hình giao dịch cặp đơn giản đầu tiên của chúng tôi.

Tránh quá tải

Trước khi kết thúc cuộc thảo luận, tôi muốn thảo luận về quá phù hợp đặc biệt. quá phù hợp là cái bẫy nguy hiểm nhất trong các chiến lược giao dịch. thuật toán quá phù hợp có thể hoạt động rất tốt trong backtest nhưng thất bại trên dữ liệu vô hình mới - có nghĩa là nó không thực sự tiết lộ bất kỳ xu hướng nào của dữ liệu và không có khả năng dự đoán thực sự. Hãy đưa ra một ví dụ đơn giản.

Trong mô hình của chúng tôi, chúng tôi sử dụng các tham số lăn để ước tính và tối ưu hóa chiều dài cửa sổ thời gian. Chúng tôi có thể quyết định đơn giản lặp lại trên tất cả các khả năng, một khoảng thời gian cửa sổ thời gian hợp lý, và chọn thời gian theo hiệu suất tốt nhất của mô hình của chúng tôi. Hãy viết một vòng lặp đơn giản để ghi điểm chiều dài cửa sổ thời gian theo pnl của dữ liệu đào tạo và tìm vòng lặp tốt nhất.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Bây giờ chúng tôi kiểm tra hiệu suất của mô hình trên dữ liệu thử nghiệm, và chúng tôi thấy rằng chiều dài cửa sổ thời gian này không phải là tối ưu! Điều này là bởi vì lựa chọn ban đầu của chúng tôi rõ ràng quá phù hợp với dữ liệu mẫu.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Rõ ràng là dữ liệu mẫu phù hợp với chúng ta sẽ không phải lúc nào cũng mang lại kết quả tốt trong tương lai.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

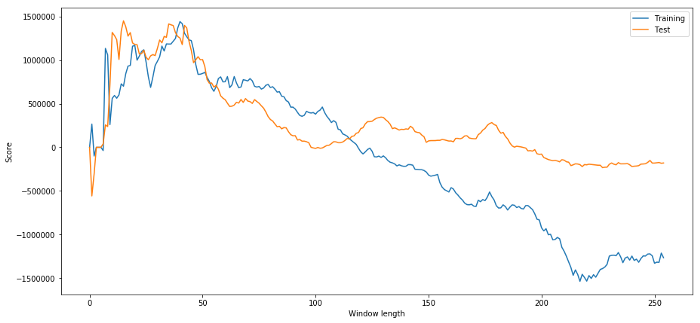
Chúng ta có thể thấy rằng bất cứ thứ gì từ 20 đến 50 là một lựa chọn tốt cho các cửa sổ thời gian.

Để tránh quá phù hợp, chúng ta có thể sử dụng lý luận kinh tế hoặc bản chất của thuật toán để chọn độ dài của cửa sổ thời gian. Chúng ta cũng có thể sử dụng bộ lọc Kalman, không yêu cầu chúng ta xác định độ dài; Cách tiếp cận này sẽ được mô tả sau trong một bài viết khác.

Bước tiếp theo.

Trong bài viết này, chúng tôi đề xuất một số phương pháp giới thiệu đơn giản để chứng minh quá trình phát triển các chiến lược giao dịch. Trong thực tế, nên sử dụng thống kê phức tạp hơn. Bạn có thể xem xét các tùy chọn sau:

• Tỉ số Hurst;

• Thời gian bán hủy của sự hồi quy trung bình được suy luận từ quy trình Ornstein-Uhlenbeck;

• Bộ lọc Kalman.

Có liên quan

Thêm nữa