【中性对冲统计套利New】(Pure-Alpha 梦幻版)
-0多空敞口暴露的中性对冲统计套利策略
各位交易者大家好,经过数个月的调试、优化与迭代,很高兴这款中性对冲统计套利已经达到了较为稳定的层面并可以与大家见面。这是一款基于多空对冲的市场中性策略,在同一账户中做多一篮子品种做空一篮子品种,多空价值相等。在避免市场β性系统性风险的前提下,运用统计方法寻找各种多空配对组合,达到α稳定盈利的低风险类型套利策略。本款策略持有体验较好,与市场大盘相关性较低,多空敞口中性,完全没有312/519等极端黑天鹅下的风险,反而会在这种市场定价错误完全混乱的时间大放异彩。下面将对这款策略做详细的说明。
Hello~Welcome come to my channel!
欢迎各位交易者来到我的频道,我是作手君,一名Quant Developer,全栈开发CTA & HFT & Arbitrage等交易策略。 感谢FMZ平台,我会在我的量化频道多多分享量化开发相关内容,同各位交易者共同维护量化社区的繁荣。
更多信息,移步我的频道哦~在这等你来撩【作手君量化小屋】
一,统计套利的介绍与说明
统计套利策略是一种利用不同篮子品种之间的价格关系进行交易的策略。该策略基于统计学原理,通过分析多个品种之间的历史价格走势和相关性,找到它们之间的价格差异,并利用这些差异进行交易。历史上,统计套利策略在股票市场得到了广泛应用。最早的统计套利策略主要是在股票之间进行,比如石油公司之间或者电信公司之间。这些策略往往基于行业相关性的假设,通过买入价格低估的股票,同时卖出价格高估的股票,以达到套利的目的。
随着市场的发展,统计套利策略也逐渐扩展到其他金融市场,如商品期货、外汇以及加密货币等。在这些市场中,可以找到存在相关性的不同篮子组合,利用价格差异进行套利交易。该策略的逻辑是基于均值回归的原理。当构建的多个篮子品种组合之间的价格出现偏离其统计范畴的情况时,存在回归的趋势。根据这一趋势,可以在价格偏离较大的时候卖出价格高的一篮子品种,并买入价格低的一篮子品种,以期针对市场短暂的错误定价进行对冲交易。通过这种方式,可以获得多篮子配对组合价差的收益。
二,统计套利的优点与缺点
优点: * 降低市场风险: 统计套利策略基于各篮子品种组合间差异的套利交易,相对于单一品种交易,分散了风险,减少了市场波动对策略的影响。减少了市场系统性风险。 * 稳定收益: 统计套利策略针对市场短期的错误定价进行回归套利交易,相对于方向性策略,具有较为稳定的收益特征。相比较方向性策略,产生更为低风险、低波动、和稳定的收益。 * 可以适应不同市场环境: 统计套利策略可以在不同的市场环境下运作,因为这种交易策略与市场的方向性关系较小。
缺点: * 历史数据只能反映过去关系,无法完全代表未来,存在一定风险。统计套利策略的构建会使用大量的统计检验,基于历史大数据进行篮子品种的组合与相关关系挖掘,未来可能产生变化,有一定的尾部风险。 * 针对市场存在的短期定价错误失衡回归均衡关系,需要的时间跨度难以准确判断。如果交易时间过长,资金使用成本也是很大的考研。 * 高要求的数据分析与模型构建能力: 统计套利策略需要对不同篮子组合品种之间的相关性、协整性等统计数据进行深入分析和建模,需要具备较高的数据分析和模型构建能力。 * 交易执行与流动性风险: 由于是多品种对冲交易,执行价格和成交量可能会受到不同品种的影响,存在交易执行风险。需要更为精妙的策略设计与架构实现。
三,本款Alpha统计套利的主要内容
1, 实时监控全品种数据信息,进行大数据扫描,构建多空品种篮子组合。
具体会构建组合篮子配对:例如有A,B,C,D,E,F6个品种,可以每分2组,每组3个品种,构建篮子组合。同时会构建指数套利:将部分行业与板块品种一分为二,构建两个新的市场指数,然后对这两个指数进行之后的统计数据分析。
2, 检验篮子多空组合相关性。
相关性是指两个或多个变量之间的关联程度。它用来衡量一个变量的变动与另一个变量的变动之间的关系,有助于判断是否存在某种对应关系或者预测一个变量的变动对另一个变量的影响。相关系数是衡量相关性的常用方法,常见的有皮尔逊相关系数(Pearson correlation coefficient)、斯皮尔曼等级相关系数(Spearman’s rank correlation coefficient)等。皮尔逊相关系数是针对两个连续型变量的关系进行评估,而斯皮尔曼等级相关系数则适用于两个有序变量的关系评估。相关系数的取值范围是[-1, 1],其中-1表示负相关,1表示正相关,0表示没有相关性。相关系数越接近-1或1,表示相关性越强;接近0表示相关性越弱。相关系数的数学公式如下(以皮尔逊相关系数为例):
r = cov(X, Y) / (std(X) * std(Y))。
其中,r为相关系数,cov为协方差,std为标准差,X和Y分别表示两个变量。在检验相关性时,常用的方法是计算相关系数的统计显著性。通常可以使用假设检验来判断相关系数是否显著。假设检验的零假设为变量之间不存在相关性,通过计算相关系数的统计量来判断是否拒绝零假设。
3, 检验篮子多空组合协整性。
协整性(cointegration)是指两个或多个时间序列变量之间的长期关系,即它们的线性组合是稳定的。相比于相关性,协整性更加关注长期的均衡关系,而不仅仅是短期的关联程度。当他们偏离这个均衡关系时,则存在校正机制使得偏离回归到合理范围。协整性的概念最初由斯皮格尔曼(S.G.Engle)和格兰杰琼(C.W.J.Granger)于1987年提出,用于解决时间序列分析中存在的伪回归问题。伪回归问题是由于变量之间可能存在单位根(unit root)而导致的,单位根使得变量间的回归关系在短期内看似显著,但在长期内并不存在真正的均衡关系。
协整理论从分析时间序列的非平稳性入手,探求非平稳变量蕴含的长期均衡关系。如果涉及的变量经过一阶差分后是平稳的,并且这些变量的某种线性组合是平稳的,则称这些变量之间存在协整性。协整为了刻画两个或多个序列之间的平稳关系。对于每一个序列单独来说可能是非平稳的,这些序列的各阶矩,如均值、方差或协方差随着时间而变化,而这些时间序列的线性组合序列却可能有不随时间变化的性质。当两个资产价格服从协整关系的时候,那么其线性组合满足均值回复(mean reverting)的性质。协整性的数学公式表达如下(以两个时间序列变量为例):
Y_t = β_0 + β_1 * X_t + ε_t
其中,Y_t和X_t分别表示两个时间序列变量的观测值,β_1是回归系数,ε_t是误差项。如果Y_t和X_t之间存在协整关系,那么两个变量的线性组合将是稳定的,即ε_t是平稳的。满足均值为0的正太分布。在检验协整性时,通常需要进行稳定性检验,常用的方法包括Johansen检验和Engle-Granger检验。Johansen检验是基于特征根(eigenvalue)的方法,可以直接检验多个变量之间的协整关系。Engle-Granger两步法检验是基于修正的OLS估计(Ordinary Least Squares)的方法,适用于两个变量之间的协整关系检验。
4,本策略会针对大量组合进行时间序列的协整关系的检验,具体标准如下:
- 单独的组合篮子时间价格序列是一阶单整向量,即时间价格序列是非平稳的(有明显趋势的)。用ADF单位根检验多个时间价格时间的平稳性。
- 单独的组合篮子一阶差分后的序列(即导数)是平稳的。用ADF单位根检验两个篮子时间价格序列。用ADF单位根检验两个篮子时间价格序列一阶差分的平稳性。
- 配对组合时间价格序列的某种线性组合是平稳的,即以两个序列构建的线性方程的残差是平稳的。对两个同阶的序列,进行OLS回归,再检验残差的平稳性。
- 更多统计检验与数据分析不再赘述,会对全市场全品种进行大规模细致的全方位统计分析。
5,进行大量Hurst指数检验。
Hurst指数用于衡量时间序列的长期记忆性,以确定序列的均值回归特性。Hurst指数值介于0和1之间,接近0.5表示序列呈现随机漫步,接近1表示具有持续趋势。原理:Hurst指数通过计算序列的重叠子序列的离差范围与其长度的关系,来估计序列长期记忆性的程度。数学公式:计算Hurst指数的一种方法是利用重叠子序列的离差范围与长度的关系,建立随机游走的对应关系。可以使用重叠子序列的离差范围与长度之间的线性回归拟合来估计Hurst指数。
6,均值回归半衰期估计。
均值回归半衰期是用来估计价格序列恢复到其均值所需时间的指标。半衰期越小,说明均值回归速度越快。原理:均值回归半衰期的计算是通过拟合收敛的指数平滑移动平均模型(EMA)来估计。当价格序列对均值的偏离超过半衰期时,可以认为存在均值回归的机会。数学公式:均值回归半衰期的计算公式如下:
(H = -\frac{\ln(0.5)}{\ln(\frac{P_t}{Pt - P{t-1}})})
检验方式:可以计算价格序列的EMA,然后基于EMA来计算半衰期。
7,依据大量统计数据构建交易策略。
简单描述,依据Hurst指数排序过滤篮子品种组合,依据均值回归半衰期估计相关统计参数,依据协整性构建交易策略组合,更多细节不会描述。
设x,y分别是资产X篮子和Y篮子的价格时间序列,二者的协整关系可以表示为:Lny = a + blnx + c,其中c为残差项,是平稳的,满足均值为0的正太分布。
经过协整检验,资产X与Y的时间价格存在协整关系,残差项c的标准差为σ,选定常数λ作为边界值。 * 当lny-(a+blnx) > λσ 时,篮子Y价格相对高估,篮子X价格相对低估,买入篮子X,卖出篮子Y; * 当lny-(a+blnx) < -λσ 时,篮子X价格相对高估,篮子Y价格相对低估,买入篮子Y,卖出篮子X; * 当价差lny-(a+blnx)回归到一定范围,比如【-0.5λσ, 0.5λσ】区间进行平仓;
8,一些特点。
当前版本已较为完善,包括超强的近乎全市场交易、对交易任务与盘口高频趋势进行估计从而进行高频的Maker结合Taker的成交优势、长期概率优势验证后的单品种的尾部对冲保护、极致的逐个订单本地记录可以与别的策略混合对冲运行等等不再赘述。
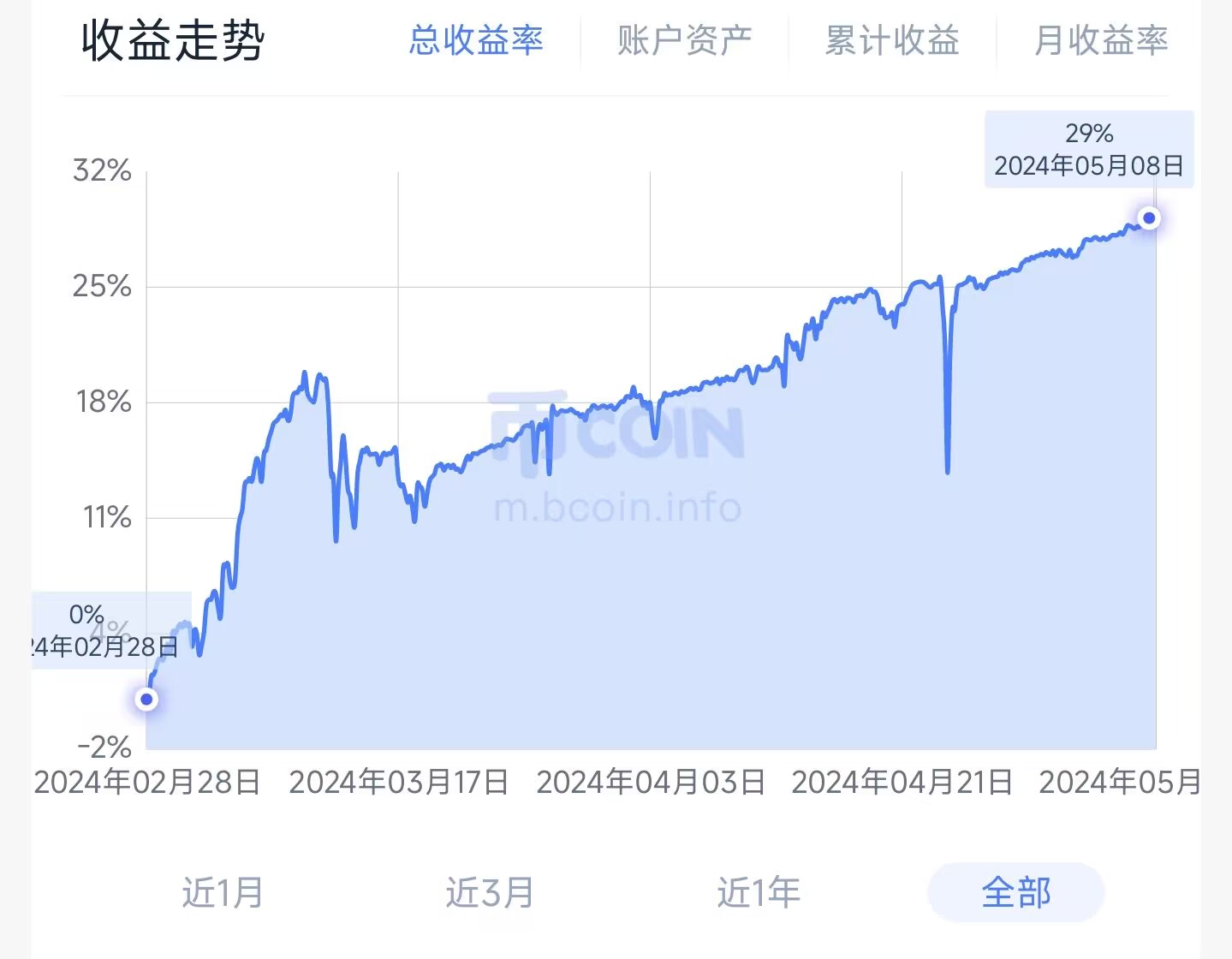
四,部分历史业绩(分钟级切片统计,真实成交价估计后的吃单万5成本数据)




五,期待合作交流,共同学习进步
第三方币coin数据
任何策略都有其方法论与适应与否的行情。例如均值回归策略依据市场随机游走等理论,动量趋势策略依据多种行为金融学理论市场存在肥尾波动的行情等。一定要了解其原理,依据其特性,适应其波动。同时策略的使用者一定要注意盈亏同源,更高的收益一定伴随着更高的风险,成熟的策略有其优势与弊端,合理的运用并扬长避短,知晓其对与错,合适与否行情下的完整表现,做到胸有成竹,宠辱不惊。
量化不是永动机,也不是万能的,但它一定是未来交易的方向,值得每个交易者学习和使用!欢迎各位交易者前来指出不足,共同讨论,一起学习进步,在波澜壮阔的行情里乘风破浪,砥砺前行。
● 本款策略较为特性,与传统趋势、网格、高频、套利等差异较大,容量有限,自营为主,欢迎大额用户与机构投资者交流学习。
● 更多合作方案:对于任何有需求的个人与机构都保持开放共赢的合作态度,期待您的商讨,按您需求、风险偏好等定制化合作。
如果您风险偏好较高,喜欢短期盈亏,有短期交易的需求,可以查看另一款稳定的高频策略,月化3%-50%,无爆仓风险: 【高频对冲做市网格New】(HFT Market-Making矿机版)
如果您资金额度较大,可以与观察另外一款大容量中低频复合CTA交易系统,历时1000天实盘,风雨无阻。是目前公布的时间最长、稳定性较高、普适性较强的CTA策略组合系统,以实现中长期稳定增长: 【复合CTA交易系统New】(多因子+多品种+多策略公用版)
✱ 联系方式 (欢迎交流讨论,共同学习进步) WECHAT: haiyanyydss Telegram: https://t.me/JadeRabbitcm 更多干货 ➔ 作手君的量化小屋 https://www.fmz.com/market-offer/512 ✱Fully automatic CTA & HFT & Arbitrage trading system @2018 - 2024