在上一篇文章中(https://www.fmz.com/digest-topic/4187)，我们介绍了配对交易策略，并演示了如何利用数据和数学分析来创建和自动化交易策略。

多空均衡权益策略是适用于一篮子交易标的的配对交易策略的自然延伸。其特别适用于品种众多且有相互关联性的交易市场,比如数字货币市场和商品期货市场.

基本原则

多空均衡权益策略是同时做多和做空一篮子交易标的。就像配对交易一样，确定哪种投资标的价格便宜，哪种投资标的价格昂贵.不同的是,多空均衡权益策略会将所有投资标的排在一个选股池中，以确定哪些投资标的相对便宜或者昂贵。然后，它将基于排名做多头部前n个投资标的，并且以等金额做空底部n个投资标的（多头头寸的总值=空头头寸的总值）。

还记得我们之前说配对交易是一个市场中立的策略吗？多空均衡权益策略也是如此，因为多头和空头头寸等额确保策略将保持市场中性（不受市场波动影响）。该策略在统计上也很稳健;通过对投资标的进行排名并持有多个头寸，你可以对你的排名模型进行多次开仓，而不仅仅是一次性风险开仓。你纯粹押注的只有你排名方案的质量。

什么是排名方案？

排名方案是可以根据预期的表现为每个投资标的分配优先级的模型。其中的因子可以是价值因子，技术指标，定价模型或上述所有因子的组合。例如，你可以使用动量指标对一系列趋势跟踪投资标的进行排名：预计具有最高势头的投资标的将继续表现良好并获得最高排名; 动量最小的投资标的表现最差，收益率最低。

该策略的成功几乎完全在于所使用的排名方案,即你的排名方案能够将高绩效投资标的与低绩效投资标的分开，更好地实现多空投资标的策略的回报。因此，制定排名方案非常重要。

怎样制定排名方案？

一旦我们确定了排名方案，我们显然希望能够从中获利。我们这样做是通过投入相同数量的资金来做多排名靠前的投资标的，并做空排名底部的投资标的。这确保了策略只会按照排名的质量按比例赚钱，并且将是"市场中立"的。

假设你正在对所有投资标的m进行排名，有n美元投资，并希望持有总共2p（其中m> 2p）的仓位。如果排名rank 1的投资标的预计会表现最差，那么排名为m的投资标的预计将表现最佳：

• 你将投资标的排列为:1,…,p这样的位置，做空2/2p美元的投资标的

• 你将投资标的排列为:m-p,…,m这样的位置，做多n/2p美元的投资标的

**注意：**由于价格跳动导致的投资标的价格不会总是均匀地划分n/2p，并且必须以整数购买某些投资标的，所以会有一些不精确的算法，算法应尽可能接近这个数字。对于运行n = 100000和p = 500的策略，我们看到:

n/2p = 100000/1000 = 100

这对于价格大于100的分数会造成很大的问题(如商品期货市场)，因为你不能开仓分数价格的仓位(数字货币市场这个问题不存在)。我们通过减少分数价格交易或增加资本来缓解这种情况。

让我们来看一个假设的例子吧

• 在发明者量化平台搭建我们的研究环境

首先,为了工作的顺利进行,我们需要搭建我们的研究环境,本文我们使用发明者量化平台(FMZ.COM)进行研究环境的搭建,主要是为了后期可以使用此平台的方便快捷的API接口和封装完善的Docker系统.

在发明者量化平台的官方称呼中，这个Docker系统被称为托管者系统。

关于如何部署托管者和机器人，请参考我之前的文章：https://www.fmz.com/bbs-topic/4140

想购买自己云计算服务器部署托管者的读者，可以参考这篇文章：https://www.fmz.com/bbs-topic/2848

在成功部署好云计算服务与托管者系统后，接下来，我们要安装Python目前最大的神器：Anaconda

为了实现本文所需的所有相关程序环境（依赖库，版本管理等），最简单的办法就是用Anaconda。它是一个打包的Python数据科学生态系统和依赖库管理器。

关于Anaconda的安装方法，请查看Anaconda官方指南：https://www.anaconda.com/distribution/

本文还将用到numpy和pandas这两个目前在Python科学计算方面十分流行且重要的库.

以上这些基础工作也可参考我之前的文章,里面有关于如何设置Anaconda环境和numpy和pandas这两个库的介绍,详情请见: https://www.fmz.com/digest-topic/4169

我们生成随机投资标的和随机因子，对其进行排名。让我们假设我们未来的回报实际上取决于这些因子值。

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

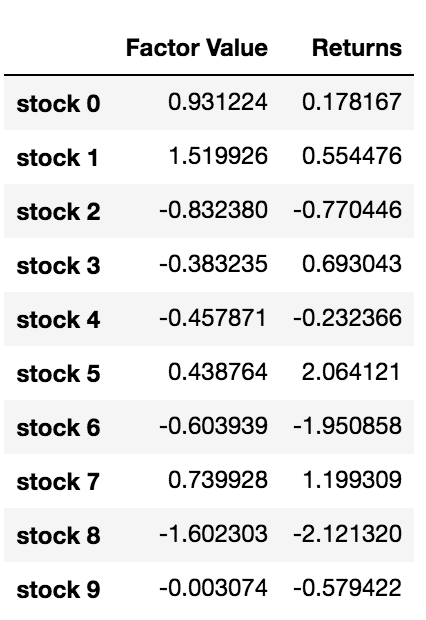
现在我们有因子价值和收益了，我们可以看到如果我们根据因子价值对投资标的进行排名，然后开仓多头和空头头寸会发生什么。

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

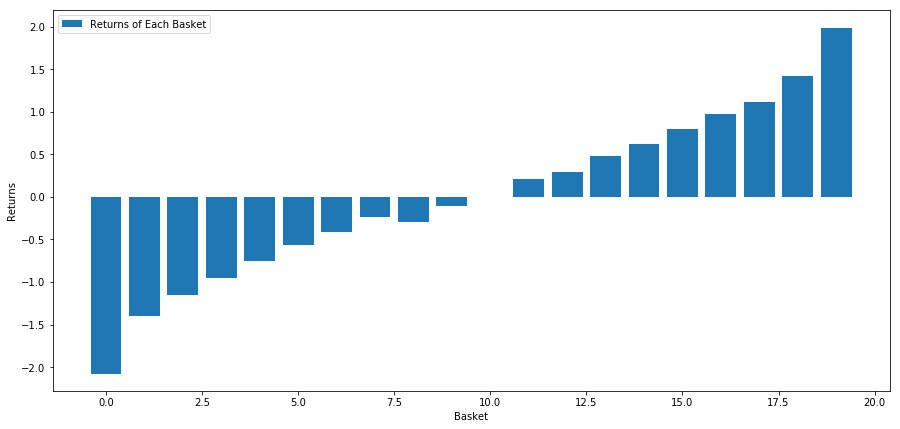
我们的策略是在一篮子投资标的池中做多排名第一的;做空排名第10的。这个策略的回报是：

basket_returns[number_of_baskets-1] - basket_returns[0]

其结果为:4.172

把钱放在我们的排名模型上，以让其能够从低绩效投资标的中分离高绩效投资标的。

在本文接下来的内容中，我们将讨论如何评估排名方案。基于排名的套利赚钱的好处在于它不受市场无序的影响,反而可以利用它。

让我们考虑一个现实世界的例子。

我们为标准普尔500指数中不同行业的32只股票加载数据并尝试对它们进行排名。

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

让我们以一个月时间周期的标准化动量指标作为排名依据

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

现在我们将分析我们股票的行为，看看我们的股票在市场中如何在我们选择的排名因子中运作。

分析数据

股票行为

我们看看我们选择的一篮子股票在我们的排名模型中是如何表现的。为此，让我们计算所有股票的一周远期回报。然后我们可以看看每个股票的1周前向回报与之前30天动量的相关性。表现出正相关的股票是趋势跟随，表现出负相关的股票是均值回归。

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

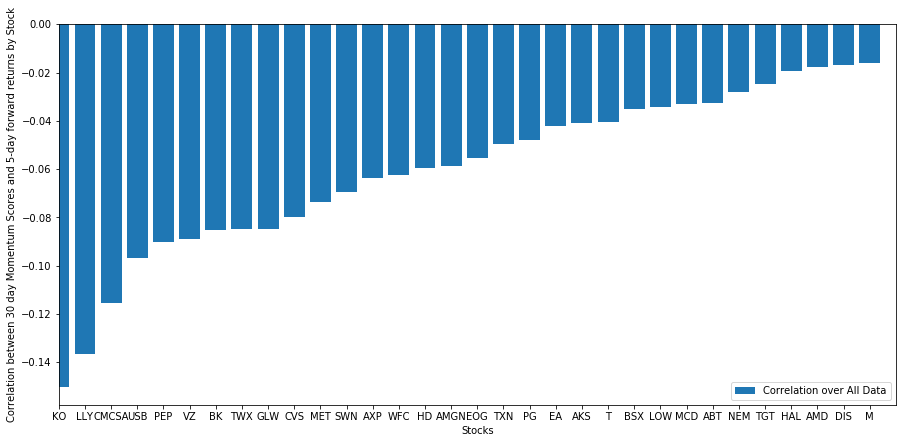
我们所有的股票都在一定程度上均值回归！（显然我们选择的宇宙就是这样运作的）这告诉我们，如果股票在动量分析中得分排名很高，我们应该预计其下周表现不佳。

动量分析得分排序与收益之间的相关性

接下来，我们需要看看我们的排名得分和市场总体的前向回报之间的相关性，即预计回报率的预测与我们的排名因子的关系,较高的相关性等级是否可以预测较差的相对回报，又或者反之亦然？

为此，我们计算所有股票的30天的动量和1周远期回报之间的每日相关性。

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

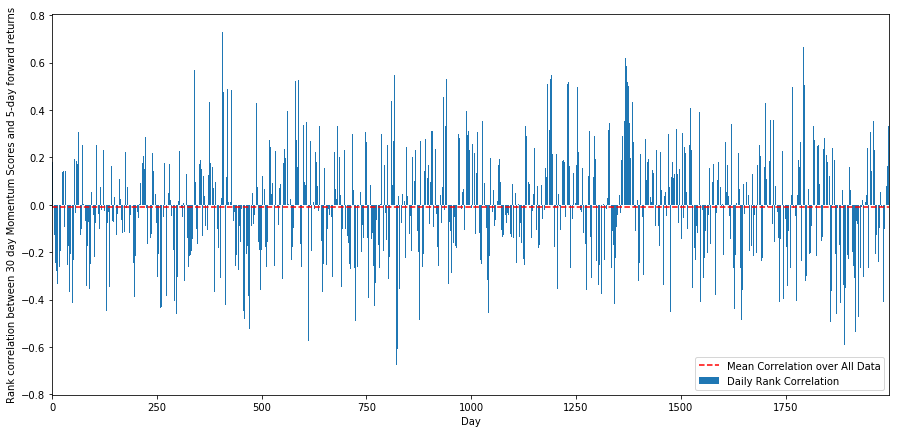
每日相关性表现的非常嘈杂，但非常轻微（这是预期到的，因为我们说过所有的股票都会均值回归）。我们还要看看1个月前向回报的平均每月相关性。

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

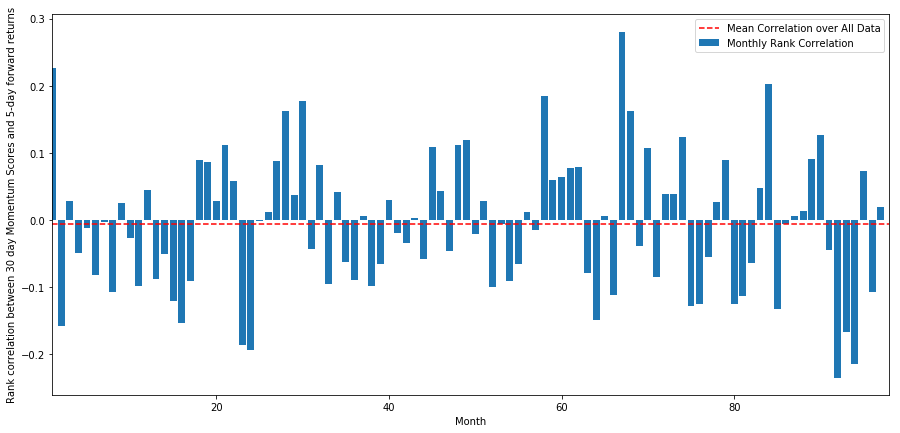
我们可以看到平均相关性再次略微为负，但每个月也会变化很大。

平均一篮子股票回报率

我们已经计算了从我们的排名中取出的一篮子股票的回报。如果我们对所有股票进行排名然后将它们分成nn组，那么每组的平均收益是多少？

第一步是创建一个函数，该函数将给出每月给定的每个篮子的平均回报和排名因子。

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

我们根据此分数对股票进行排名时计算每个篮子的平均回报。这应该让我们可以了解很长一段时间内他们的关系。

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

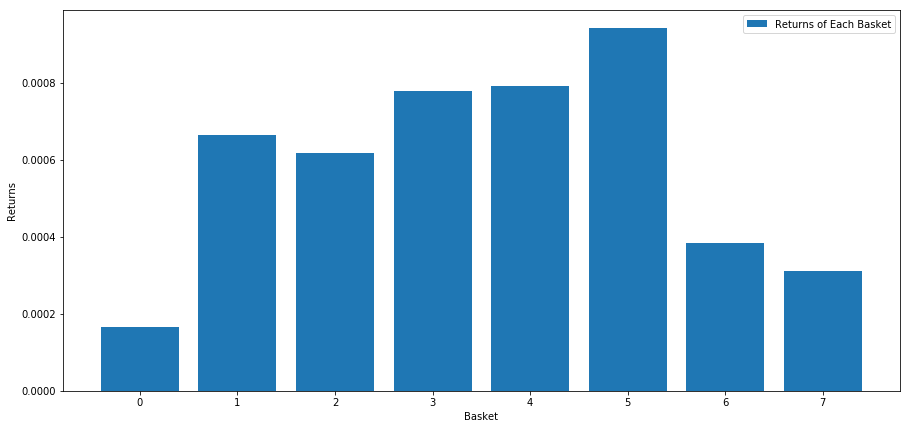
似乎我们能够将高绩效者与低绩效者分开了。

利差(基差)一致性

当然，这些只是平均关系。为了了解这关系是多么一致，以及我们是否愿意进行交易，我们应该随着时间的推移来改变看待它的方法和态度。接下来，我们将查看它们前两年的月度利差(基差)。我们可以看到更多变化，进行进一步的分析以确定这个动量分数是否可以交易。

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

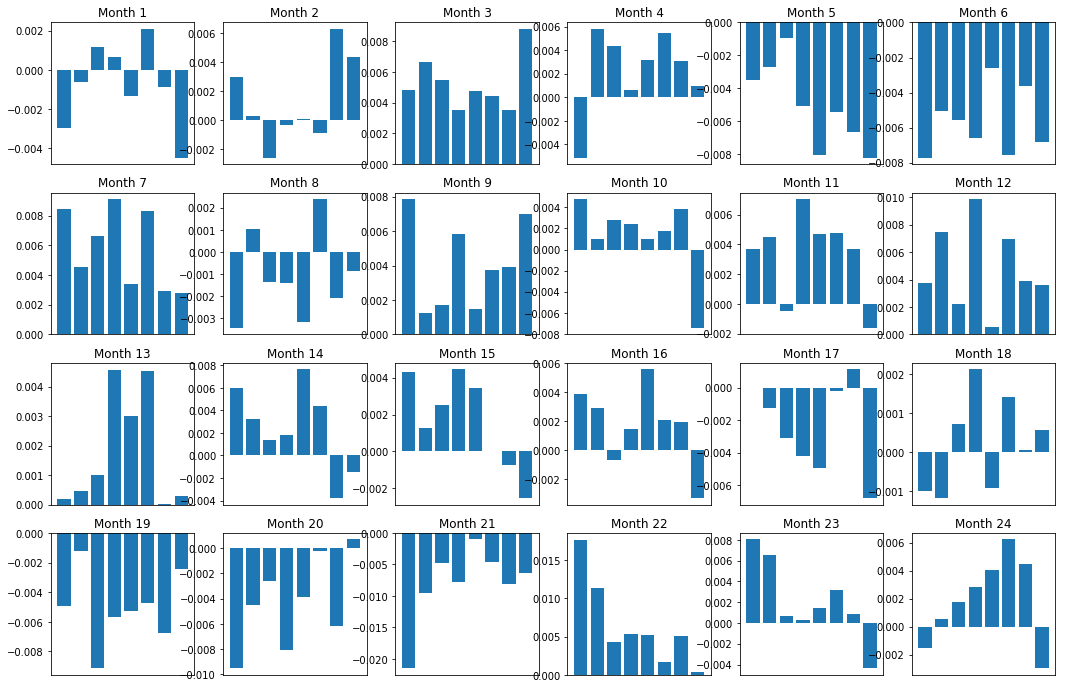
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

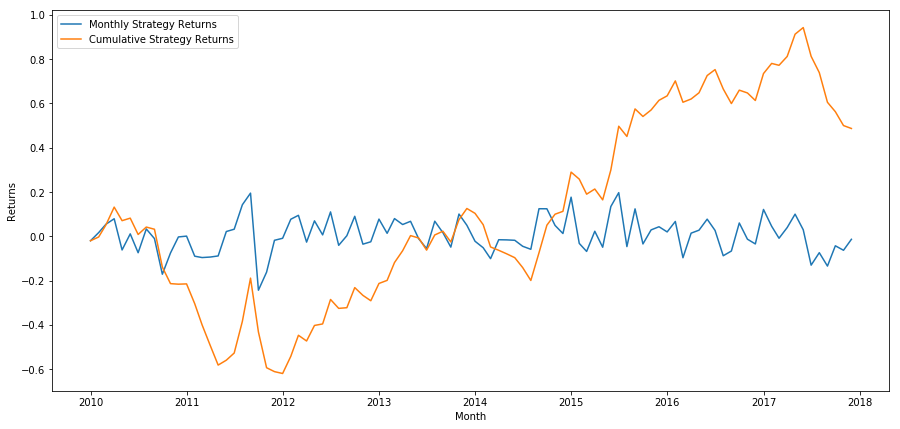
最后，如果我们做多最后一个篮子并且每个月做空第一个篮子，那么让我们看一下回报（假设每个证券的资本分配相等）

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

年回报率：5.03%

我们看到，我们有一个非常微弱的排名方案，只能温和地将高绩效股票与低绩效股票区分开来。 此外，这个排名方案没有一致性，每月变化很大。

找到正确的排名方案

要实现多空均衡权益策略，你实际上只需要确定排名方案。之后的一切都是机械的。一旦你有一个多空均衡权益策略，你可以交换不同的排名因子，别的都不用太大的改动。这是一种非常方便的方法，可以快速迭代你的想法，而无需担心每次调整全部代码。

排名方案也可以来自几乎任何模型。它不一定是基于价值的因子模型，它可以是一种机器学习技术，可以提前一个月预测回报并根据该等级进行排名。

排名方案的选择与评估

排名方案是多空均衡权益策略的优势所在，也是最重要的组成部分。选择一个好的排名方案是一个系统的工程，并没有简单的答案。

一个很好的起点是选择现有的已知技术，看看你是否可以稍微修改它们以获得更高的回报。 我们将在这里讨论几个起点：

• 克隆和调整：选择一个经常讨论的内容，看看是否可以稍微修改它以获得优势。通常情况下，公开的因子将不再有交易信号，因为它们已完全套利出市场。但是，有时它们会引导你朝着正确的方向前进。

• 定价模型：任何预测未来回报的模型都可能是一个因子,都有潜在的可能用于对你的一篮子交易标的进行排名。你可以采用任何复杂的定价模型并将其转换为排名方案。

• 基于价格的因子（技术指标）：基于价格的因子，如我们今天所讨论的，获取有关每种权益的历史价格的信息，并使用它来生成因子价值。例子可能是移动平均指标，动量指标或波动率指标。

• 回归与动量：值得注意的是，有些因子认为价格一旦朝着一个方向发展，就会继续这样做。有些因子恰恰相反。两者都是关于不同时间范围和资产的有效模型，并且研究基础行为是基于动量还是基于回归是很重要的。

• 基本因子（基于价值）：这是使用基本价值的组合，如PE，股息等。基本价值包含与公司的现实世界事实相关的信息，因此在许多方面可以比价格更强大。

最终，发展预测因子是一场军备竞赛，你正试图保持领先一步。因子会从市场中被套利并且具有使用寿命，因此你必须不断地开展工作以确定你的因子经历了多少衰退，以及可以使用哪些新因子来取代它们。

其他考虑因素

• 重新平衡频率

每个排名系统都会在稍微不同的时间范围内预测回报。基于价格的均值回归可能在几天内可预测，而基于价值的因子模型可能在几个月内具有预测性。确定模型应该预测的时间范围非常重要，并在执行策略之前进行统计验证。你当然不希望通过尝试优化重新平衡频率来过度拟合,你将不可避免地找到一个随机优于其他频率.一旦确定了排名方案预测的时间范围，尝试以大约该频率进行重新平衡，以便充分利用你的模型。

• 资本能力和交易成本

每种策略都有最小和最大的资本容积,最低门槛通常由交易成本决定。

交易太多股票将导致高交易成本。假设你想购买1000股，那么每次重新平衡将产生几千美元的成本。你的资本基础必须足够高，以使交易成本占你的策略产生的回报的一小部分。例如，如果你的资本为100,000美元且你的策略每月赚取1％（1000美元），则所有这些回报将被交易成本占用。你需要以数百万美元的资本运行该策略获利超过1000股。

最低的资产门槛，主要取决于交易的股票数量。然而，最大容量也非常高，多空均衡权益策略能够交易数亿美元而不会失去优势。这是事实，因为该策略相对不经常重新平衡.总资产数量除以交易的股票数量,每股的美元价值会非常低，你不必担心你的交易量会影响市场。假设你交易1000股，也就是100,000,000美元。如果你每个月重新平衡整个投资组合，那么每个股票每月会只交易100,000美元，这对于大多数证券而言不足以成为重要的市场份额。

Related

More