এফএমইএক্স-এর পতন অনেক লোককে প্রতারিত করেছে, কিন্তু এটি সম্প্রতি একটি পুনঃসূচনা পরিকল্পনা নিয়ে এসেছে এবং ঋণ আনলক করার জন্য মূল খনির অনুরূপ নিয়ম প্রণয়ন করেছে। লেনদেন খনির বিষয়ে, একটি বিশ্লেষণ নিবন্ধ দেওয়া হয়েছে, https://www.fmz.com/bbs-topic/5834। বাছাই করা খনির মধ্যে অপ্টিমাইজেশনের জন্যও জায়গা রয়েছে। যদিও লোকেদের একই গর্তে দুবার পা দেওয়া উচিত নয়, যারা FMEX-এ দাবি করেছেন তারা নির্দিষ্ট রিয়েল-টাইম কৌশলগুলি দেখতে চান যা FMZ পরিমাণগত প্ল্যাটফর্মে চলতে পারে।

FMEX বাছাই আনলক করার নিয়ম

প্রতিটি দিনের প্রতি 5 মিনিটকে একটি বাছাই এবং আনলক করার সময়কাল হিসাবে সংজ্ঞায়িত করুন এবং প্রতিটি সময়কাল সেই দিনের জন্য ট্রেডিং পেয়ারের বাছাই এবং আনলক করার পরিমাণের 1/288 বরাদ্দ করা হয়। প্রতিটি চক্রে, ট্রেডিং পেয়ারের জন্য মুলতুবি ক্রয়-বিক্রয়ের অর্ডারগুলির একটি স্ন্যাপশট তৈরি করতে একটি সময় বিন্দু এলোমেলোভাবে নির্বাচন করা হয়, যেখানে:

• কিনুন 1. ব্যবহারকারীর মুলতুবি অর্ডারের পরিমাণের অনুপাত অনুসারে, এই সাজানোর আনলকিং চক্রে ফেরতের পরিমাণের 1/4 বরাদ্দ করা হবে।
• বিক্রয় 1 ব্যবহারকারীর মুলতুবি অর্ডার পরিমাণের অনুপাতে, এই সাজানোর আনলকিং চক্রের 1/4 টাকা ফেরত দেওয়া হয়।
• বাই 2 থেকে বাই 5 পর্যন্ত মুলতুবি থাকা অর্ডারের চারটি স্তরের জন্য, সাজানো আনলক চক্রের ফেরতের পরিমাণের 1/40 প্রতিটি স্তরে ব্যবহারকারীর মুলতুবি অর্ডারের পরিমাণ অনুযায়ী বরাদ্দ করা হবে।
• সেল 2 থেকে সেল 5 পর্যন্ত মুলতুবি থাকা অর্ডারের চারটি স্তরের জন্য, সাজানো আনলক চক্রের ফেরত পরিমাণের 1/40 প্রতিটি স্তরে ব্যবহারকারীর মুলতুবি অর্ডারের পরিমাণ অনুযায়ী বরাদ্দ করা হবে।
• বাই 6 থেকে বাই 10 পর্যন্ত পাঁচটি স্তরের মুলতুবি অর্ডারগুলির জন্য, সাজানো আনলক চক্রের ফেরতের পরিমাণের 1/50 প্রতিটি স্তরে ব্যবহারকারীর মুলতুবি অর্ডারের পরিমাণ অনুযায়ী বরাদ্দ করা হবে।
• সেল 6 থেকে সেল 10 পর্যন্ত মুলতুবি থাকা অর্ডারের পাঁচটি স্তরের জন্য, সাজানো আনলক চক্রের ফেরতের পরিমাণের 1/50 প্রতিটি স্তরে মুলতুবি থাকা অর্ডারের পরিমাণের ব্যবহারকারীর অনুপাত অনুসারে বরাদ্দ করা হবে।
• 11 থেকে 15 কিনুন পর্যন্ত মুলতুবি থাকা অর্ডারগুলির পাঁচটি স্তরের জন্য, সাজানো আনলক চক্রের ফেরতের পরিমাণের 1/100 প্রতিটি স্তরে মুলতুবি থাকা অর্ডারের পরিমাণের ব্যবহারকারীর অনুপাত অনুসারে বরাদ্দ করা হবে।
• সেল 11 থেকে সেল 15 পর্যন্ত মুলতুবি থাকা অর্ডারগুলির পাঁচটি স্তরের জন্য, সাজানো আনলক চক্রের ফেরত পরিমাণের 1/100 প্রতিটি স্তরে মুলতুবি থাকা অর্ডারের পরিমাণের ব্যবহারকারীর অনুপাত অনুসারে বরাদ্দ করা হবে।

দিনে একটি নির্দিষ্ট ট্রেডিং পেয়ারে ব্যবহারকারীর সাজানো আনলকিংয়ের মোট রিটার্ন হল ব্যবহারকারীর প্রতিটি চক্রে ট্রেডিং পেয়ারের সাজানো আনলক করার মাধ্যমে ফেরত দেওয়া পরিমাণের সমষ্টি।

সুবিধাগুলি আনলক করার জন্য বাছাই করা হচ্ছে

প্রথমে সাজানো এবং আনলক করার মোট আয় হল:

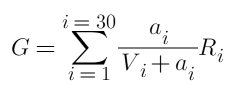
তাদের মধ্যে, i একটি অবস্থানের প্রতিনিধিত্ব করে, এবং দুটি পক্ষের মধ্যে মোট 30টি অবস্থান রয়েছে a হল মুলতুবি অর্ডারের পরিমাণ, R হল রিফান্ডের পরিমাণ এবং V হল বিদ্যমান অর্ডারগুলির মোট পরিমাণ৷

লেনদেন আনলক করার বিপরীতে, মুলতুবি অর্ডারের জন্য কোন খরচ নেই এখানে R শুধুমাত্র আপেক্ষিক আকার বিবেচনা করে, এবং USDT মূল্যের পরম পরিমাণ বিবেচনা করার প্রয়োজন নেই। যদি আমরা মুলতুবি থাকা অর্ডারের মোট সংখ্যা নির্ধারণ করি, তাহলে প্রশ্ন হয়ে যায় কিভাবে বিভিন্ন পদে অর্ডারগুলি বরাদ্দ করা যায় যাতে রাজস্ব জি সর্বোচ্চ করা যায়। ন্যূনতম পরিমাণ মুলতুবি থাকা অর্ডারগুলির সাথে কেবল অবস্থান খুঁজে পাওয়া এবং সেগুলিকে স্থাপন করা স্পষ্টতই সর্বোত্তম সমাধান নয়। উদাহরণস্বরূপ, 10 এর বিদ্যমান অর্ডার ভলিউম সহ তিনটি পজিশন রয়েছে এবং আমরা মোট অর্ডার ভলিউম 30 এ সেট করি। যদি শুধুমাত্র একটি পজিশন অর্ডার করার জন্য নির্বাচন করা হয়, তাহলে চূড়ান্ত মোট আয় হবে 0.75R প্রতিটি অবস্থান 10 সঙ্গে স্থাপন করা হয়, তারপর চূড়ান্ত আয় 1.5R এটা কখনও কখনও বিচ্ছুরিত আদেশের আয় ভাল হয় দেখা যায়. তাহলে কিভাবে তহবিল বরাদ্দ করা যায়?

বাছাই আনলকিং অপ্টিমাইজেশান

অবশেষে, আমাদের অপ্টিমাইজেশন লক্ষ্য এবং সীমাবদ্ধতা হল:

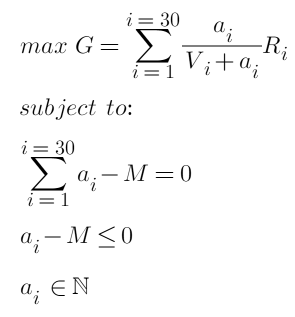
তাদের মধ্যে, M হল মোট পেন্ডিং অর্ডার ভলিউম। এটি একটি দ্বিঘাত উত্তল অপ্টিমাইজেশান সমস্যা যার মধ্যে অসমতা রয়েছে, কেটিটি শর্তকে সন্তুষ্ট করে এবং সমাধানটি একটি পূর্ণসংখ্যা। সংশ্লিষ্ট ব্যাগ এবং উত্তল অপ্টিমাইজেশান সলভার ব্যবহার করে প্রতিটি অবস্থানের জন্য সর্বোত্তম মুলতুবি অর্ডার ভলিউম ফিরিয়ে দিয়ে সরাসরি ফলাফলগুলি অর্জন করা সম্ভব হওয়া উচিত। কিন্তু এটি স্পষ্টতই আমরা যে উত্তর চাই তা নয়।

একটি সহজ উদাহরণ দিয়ে শুরু করুন

শুধুমাত্র দুটি স্তরের পরিস্থিতি বিবেচনা করুন 10 এবং 20 (যথাক্রমে প্রথম স্তর এবং দ্বিতীয় স্তর হিসাবে উল্লেখ করা হয়)। তাদের বরাদ্দ করতে তহবিল সর্বোচ্চ আনলক সীমা পৌঁছেছেন? এই প্রশ্নটি সহজ মনে হচ্ছে, কিন্তু গণনা ছাড়াই একটি সঠিক উপসংহার টানা কঠিন।

বিকল্প 1:

ন্যূনতম মুলতুবি অর্ডার অবস্থান খুঁজুন এবং মোট লাভ হবে G=30/(30+10)=0.75R। এটিও চিন্তা করার সবচেয়ে সহজ সমাধান।

দৃশ্যপট ২:

প্রতিবার 1 ইউয়ান বরাদ্দ করুন, এবং এটি এমন জায়গায় বরাদ্দ করুন যেখানে সর্বাধিক মুনাফা তৈরি করা যেতে পারে, অর্থাৎ, সবচেয়ে ছোট মুলতুবি অর্ডার সহ অবস্থান। তারপর 1ম ইউয়ান প্রথম গিয়ারে বরাদ্দ করা হবে, এবং প্রথম গিয়ারে মুলতুবি অর্ডারের পরিমাণ 10+1 হয়ে যাবে, এবং 2য় ইউয়ানও প্রথম গিয়ারে বরাদ্দ করা হবে...এবং এভাবেই, যতক্ষণ না মোট 10 ইউয়ান প্রথম গিয়ারে বরাদ্দ করা হয়েছে এই সময়ে, আপনি এলোমেলোভাবে একটি নির্বাচন করতে পারেন এবং যখন প্রথম ধাপে মুলতুবি থাকা অর্ডারের সংখ্যা 20 ছাড়িয়ে যায়, তখন সেগুলি দ্বিতীয় স্তরে বরাদ্দ করা হবে৷ চূড়ান্ত ফলাফল হল যে প্রথম স্তরটি 20 ইউয়ান বরাদ্দ করা হয়েছে, দ্বিতীয় স্তরটি 10 ​​ইউয়ান বরাদ্দ করা হয়েছে এবং তাদের চূড়ান্ত মুলতুবি আদেশ উভয়ই 30। মোট আয় G=20/30+10/30=R. এই বিকল্পটি বিকল্প 1 থেকে অনেক ভালো এবং গণনা করা সহজ।

সমাধান ৩:

আপনি ধরে নিতে পারেন যে প্রথম গিয়ারটি a বরাদ্দ করা হয়েছে, এবং দ্বিতীয় গিয়ারটি 30-a, তারপর আপনি সরাসরি সমীকরণটি তালিকাভুক্ত করতে পারেন এবং 0-এ ডেরিভেশনটি বের করতে পারেন (প্রক্রিয়াটি তালিকাভুক্ত নয়, এটি লেনদেন আনলকিং নিবন্ধের অনুরূপ) , এবং চূড়ান্ত ফলাফল গণনা করুন:

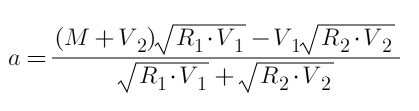
পূর্ণসংখ্যায় প্রতিস্থাপন করো এবং a=15 পাও। মোট লাভ G=15/25+15/35=1.0286R, যা বিকল্প 2 এর চেয়ে ভালো। যেহেতু এটি সরাসরি সূত্র থেকে উদ্ভূত, তাই এটিই সর্বোত্তম সমাধান। পাঠকরা এটি পরীক্ষা করে দেখতে পারেন।

ফলাফল আপনার প্রত্যাশার চেয়ে ভিন্ন হতে পারে। এটা স্পষ্ট যে পরিকল্পনা ২-এ প্রতিটি ডলার বরাদ্দ করা বর্তমান পরিস্থিতিতে সর্বোত্তম সমাধান। কেন এটি সামগ্রিকভাবে সর্বোত্তম সমাধান নয়? এই পরিস্থিতি খুবই সাধারণ। স্থানীয় সর্বোত্তমতা অগত্যা সামগ্রিক সর্বোত্তমতা নয়, কারণ বরাদ্দের আগে, অর্ডারগুলি ইতিমধ্যেই তহবিল বিনিয়োগ করেছে, এবং সামগ্রিক দক্ষতার জন্য ডুবে যাওয়া খরচ বিবেচনা করা প্রয়োজন। অপ্টিমাইজেশনের প্রতিটি ধাপের জন্য আমাদের লক্ষ্য হল একক সুবিধা সর্বাধিক করার পরিবর্তে সামগ্রিক দক্ষতা সর্বাধিক করা।

নির্দিষ্ট অপ্টিমাইজেশন পরিকল্পনা

অবশেষে, ব্যবহারিক এবং সম্ভাব্য ক্রিয়াকলাপ শুরু হয়েছে প্রতিবার 1 ইউয়ান বরাদ্দ করে সমস্যাটি সহজ করা যাক। প্রথমত, কার্যকারিতা পরিমাপ করুন প্রতিটি a-এর অবদানকে প্রতিফলিত করে। স্পষ্টতই, ফাংশনের গ্রাফ অনুসারে, a=1, উপস্থিতি থেকে অনুপস্থিতি, সর্বোচ্চ দক্ষতা, এবং তারপর ধীরে ধীরে হ্রাস পায়।

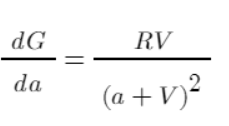
উপরের একই সাধারণ উদাহরণ ব্যবহার করে, তহবিল বরাদ্দ করার পরে দক্ষতা গণনা করুন এবং টেবিলটি তালিকাভুক্ত করুন:

তহবিল	1	2
1	0.0826	0.0454
2	0.069	0.0413
3	0.0592	0.0378
4	0.051	0.0347
5	0.0444	0.032
...	...	...
12	0.0207	0.0195
13	0.0189	0.0184
14	0.0174	0.0173
15	0.016	0.0163
16	0.0148	0.0154
17	0.0137	0.0146
18	0.0128	0.0139

টেবিল অনুসারে, 1ম ইউয়ান প্রথম বন্ধনীতে বরাদ্দ করা হয়, 2য় ইউয়ান প্রথম বন্ধনীতে বরাদ্দ করা হয়... 5ম ইউয়ান দ্বিতীয় বন্ধনীতে বরাদ্দ করা হয়... এবং শেষ পর্যন্ত 15 ইউয়ান বরাদ্দ করা হয় প্রথম বন্ধনী এবং দ্বিতীয় বন্ধনী থেকে 15 ইউয়ান, আমরা সমীকরণের উপর ভিত্তি করে গণনা করেছি সর্বোত্তম সমাধান। বিশেষত 30 তম গিয়ারের জন্য, অ্যালগরিদম একই, এবং নির্দিষ্ট পদক্ষেপগুলি হল:

• 1. প্রথমে সমস্ত গিয়ার পরীক্ষা করুন যদি V=0, তাহলে a=1, কোন অতিরিক্ত তহবিল বরাদ্দ করা হবে না।
• 2. N শেয়ারে মোট তহবিল বরাদ্দ করুন এবং প্রতিবার বরাদ্দের জন্য একটি গিয়ার নির্বাচন করুন।
• 3. প্রতিটি গিয়ারের দক্ষতা গণনা করুন =RV/pow(a+V,2), যেখানে a এই অবস্থানে জমাকৃত বরাদ্দকৃত তহবিল + এই সময়ে বরাদ্দকৃত তহবিলকে প্রতিনিধিত্ব করে।
• 4. সবচেয়ে দক্ষ গিয়ারে তহবিল বরাদ্দ করুন যদি কার্যকারিতা একই হয় তবে এলোমেলোভাবে একটি বেছে নিন।
• 5. তহবিল বিতরণ সম্পূর্ণ না হওয়া পর্যন্ত লুপ 3-4

যদি আমাদের মোট মুলতুবি অর্ডারগুলি বড় হয় এবং প্রতিটি ডলার একবার বরাদ্দ করার দক্ষতা খুব কম হয়, আমরা তহবিলগুলিকে 100টি শেয়ারে ভাগ করতে পারি এবং প্রতিবার একটি শেয়ার বরাদ্দ করতে পারি যেহেতু এটি শুধুমাত্র একটি সাধারণ গণনা এবং বাছাই, অ্যালগরিদমটি খুবই দক্ষ৷ এক্সিকিউশন লেভেলের জন্য নির্দিষ্ট, অপ্টিমাইজেশানের জন্য এখনও জায়গা আছে, যেমন আমাদের অর্ডারগুলিকে 100 তে ভাগ করা, যাতে প্রতিবার আমরা সামঞ্জস্য করি, আমাদের কেবল সেগুলিকে সরিয়ে দেওয়ার পরিবর্তে অর্ডারগুলিকে পুনরায় বিতরণ করতে হবে। বাজার থেকে দূরত্বকে আরও বেশি ওজন দেওয়ার জন্য আপনি নিজেই R মান সেট করতে পারেন।

এই নিবন্ধটি FMZ পরিমাণগত প্ল্যাটফর্মের একটি মূল নিবন্ধ হস্তান্তর করার সময় উত্সটি নির্দেশ করুন: https://www.fmz.com/bbs-topic-new/5843।