Kryptowährungen sind eine neue Anlageklasse, und Forscher beginnen gerade, die grundlegenden Kräfte hinter ihren Preisbewegungen besser zu verstehen. Eine neue Forschungsarbeit zeigt, dass die Preise von Bitcoin mit dem Metcalfe-Gesetz modelliert werden können.

Zusammenfassung:

Wir zeigen anhand von Beispielen, dass der langfristige Preis von Bitcoin nicht zufällig ist, sondern als eine Funktion der langfristigen Zunahme der Anzahl der Nutzer mit der Zeit modelliert werden kann. Anhand von beobachteten Facebook- und Bitcoin-Daten haben wir die Beziehung zwischen Preis, Anzahl der Nutzer und Zeit abgeleitet und gezeigt, dass der erhaltene Marktwert möglicherweise der Gompertz-Sigmoid-Wachstumsfunktion unterliegt. Diese Funktion wurde historisch verwendet, um das Wachstum von Organismen wie Bakterien, Tumoren und Viren zu beschreiben und könnte in der Netzeconomie eine gewisse Anwendung haben.

Bemerkenswerte Zitate aus wissenschaftlichen Studien:

In diesem Artikel wird die Preisbildung in einem aufstrebenden und oftmals missverstandenen Kryptowährungs-Ökosystem einfach erklärt. Mit Bitcoin als Beispiel liefern wir überzeugende empirische Beweise dafür, dass die Preisbildung nicht das semi-randomisierte Ergebnis von emotionalen Investitionen ist, sondern auf einem Prinzip basiert, das erst vor kurzem als wertwirtschaftlich anerkannt wurde: der Netzwerkeconomie.

Eine Untersuchung des Bitcoin-Preises lieferte einige interessante Beobachtungen, die den Mythos, dass der Bitcoin-Wert ein Rätsel ist, direkt widerlegten. Erstens, wie die Befürworter seit langem behaupten, hängt der Wert einer Währung hauptsächlich von der Verwendung und Akzeptanz der Währung ab.

Das Metcalfe-Gesetz basiert auf einem mathematischen Parameter, der die Verbindungen zwischen n Nutzern beschreibt. Daher ist der Netzwert V eine Funktion der Anzahl der Nutzern. Die mathematische Grundlage des Metcalfe-Gesetzes basiert auf Paarverbindungen (z. B. ein Telefon). Wenn vier Personen in einem Netzwerk ein Telefon benutzen, gibt es insgesamt 3 + 2 + 1 = 6 Verbindungen.

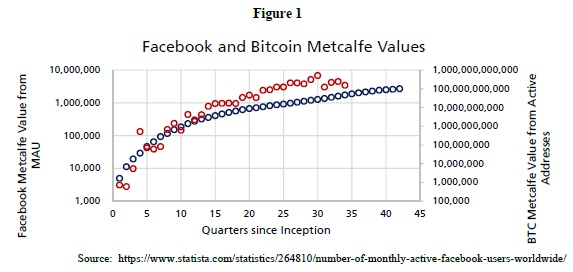
Facebook eignet sich hervorragend zum Vergleich mit Bitcoin. Die Länge jeder Datenreihe ist fast gleich (ca. 10 Jahre). Beide sind ziemlich innovativ, wenn auch nicht ganz original (Digicash vor Bitcoin, MySpace vor Facebook). Es gibt nur selten die Möglichkeit, eine Währung oder ein anderes Asset zu sehen, das mit der Zeit übernommen wird.

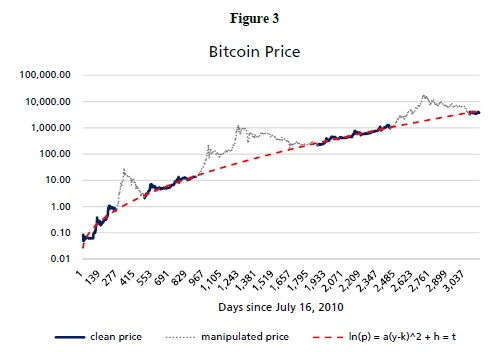
Rückblickend auf Abbildung 3 gibt es drei bemerkenswerte Ausnahmen, bei denen der Preis von Bitcoin von der Parallaxlinie abweicht. Es handelt sich um Zeiträume, in denen es zu dokumentierter Preismanipulation und schließlich zur Gleichgewichtserreichung kam. Diese Spitzen stellen Preisabweichungen dar, die nicht durch benutzerrelevante Faktoren erklärt werden können. Benutzerrelevante Faktoren werden durch Nutzerwachstum oder Netzwerknutzung getrieben.

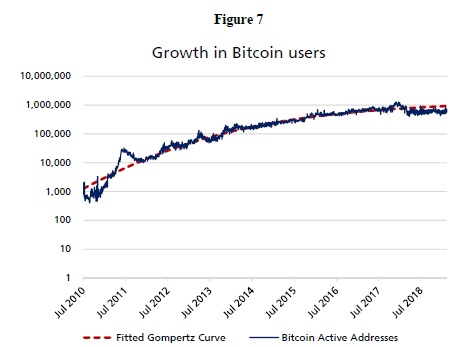
Wenn n mit einer konstanten Rate wächst, ist log (n) linear. Da log (n) nicht linear ist, wie wir es in Facebook und Bitcoin (Abbildung 7) beobachten, ist n mit einer konstanten Rate wachsend, was darauf hindeutet, dass die Annahme in verschiedenen Phasen ist. Dieses Modell der kumulativen Wachstumsrate erzeugt die S-Form-Funktion (Gompertz-Funktion), die seit Jahrzehnten verwendet wird, um Virusinfektionen, Bakterienwachstum, Tumorwachstum und Mobilfunkverbreitung zu simulieren.[2018], mit dem er Metcalfe’s Verwandtschaftskoeffizienten simuliert. Mit den täglichen Daten von n aktiven Proxy-Konten passen wir diese Gleichung zu den aktiven Adressen in Abbildung 7 an.

Das ist eine sehr schwierige Aufgabe, die sich nicht von einem einfachen Computer aus erledigen lässt.