PS: Der Artikel ist lang und nicht sehr umfangreich, ich empfehle Ihnen, ihn zu lesen, er wird Ihnen helfen.

Die Grid-Trading-Methode ist im Wesentlichen eine Handelsmethode, bei der die Preise durch wiederholte niedrige, hohe oder niedrige Kauf- und Verkaufsschwankungen mechanisch manipuliert werden. Wenn die Preise sinken, wird geteilt gekauft, wenn die Preise steigen, werden geteilt verkauft. Die Grid-Trading-Methode ist nicht auf künstliches Denken angewiesen, sondern ist eine rein prozedurale Handlung, die wie ein Fischernetz die Schwankungen der Marktlage nutzt.

Die Grid-Trading-Methode kann programmierbar betrieben werden, ohne lange Zeit zu verbringen, ohne sich um die Stabilität der Gewinne zu kümmern. Daher ist die Grid-Trading-Methode die beste Methode, um einen stabilen Gewinn zu erzielen, an dem gewöhnliche Menschen teilnehmen können, da diese Methode eine geringe Anforderungen an die Fähigkeiten der Menschen hat.

Grid-Geschäftsregeln

Ein einfaches Beispiel: Man teilt sein Geld in zwei gleiche Teile: Eine Hälfte kauft sofort die Aktien oder Fonds, die einem gefallen, und die andere Hälfte ist in der Tasche. Wenn die Aktien oder Fonds, die man kauft, ständig unter die Erde fallen, nimmt man das Geld aus der Tasche und setzt es auf. Viele Handelssoftware ist in der Regel eingebaut, die Benutzer können automatisch laufen, wenn sie einfach eingerichtet werden. Die Artikel der Gitterhandelsmethode-Universum-Kolumne-Serie enthalten ein Setup-Tutorial, das interessierte Freunde durchsuchen können, um den Inhalt der Kolumne zu lesen und direkt das Setup-Tutorial der Software zu erlernen.

Es gibt viele verschiedene Varianten der Gittermethode, und hier ist eine der bekanntesten, die die wissenschaftlichen Grundlagen für einen stabilen Gewinn der Gittermethode beschreibt und erklärt, warum immer mehr Geld in Ihrem Konto steigt.

Jeder, der eine Aktie gekauft hat, hat diese Erfahrung gemacht, eine Aktie ist nicht so leicht gestiegen, dann ist sie wieder zurückgefallen, hat sich mühsam gearbeitet, hat es heimlich bereut und hat es früh verkauft.

In der zweiten Hälfte seines Lebens widmete sich Shannon hauptsächlich der Erforschung von Investments und hielt regelmäßig Vorträge, in denen er den Leuten die Geheimnisse der Investition beibrachte. Ein Jahr später hielt er eine Rede in der größten Auditorium des MIT, in der er den Leuten die Geheimnisse des Geldes verdienen unterrichtete.

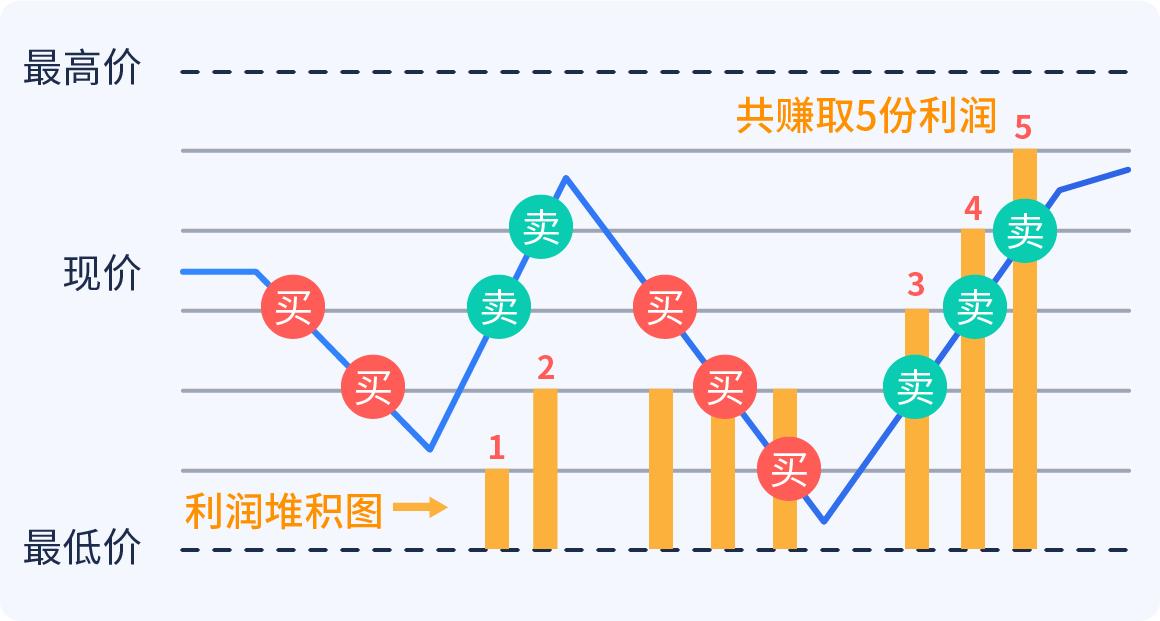
Die Nachfolger dieses Geheimnisses nannten es den Teufel von Shannon, und der Teufel von Shannon ist eine Art von Gitterhandel, von dem man so oft spricht.

Das Rezept von Shannon lautet:

Was würden Sie tun, wenn eine Aktie von 1 auf 2 steigen würde und dann von 2 auf 1 fallen würde?

Wenn Sie 200 Dollar investieren wollen, dann ist Shannon’s Tipp, dass Sie 100 Dollar für die Aktien und 100 Dollar für die Leerstände kaufen, und dann müssen Sie die Aktien so halten, dass der Marktwert und die Summe des Geldes gleich sind.

Wenn Sie 100 Aktien haben, die auf 200 gefallen sind, dann haben Sie insgesamt 200 Aktien plus 100 Bargeld, also 300 Aktien, dann verkaufen Sie 50 Dollar für die Aktie, also haben Sie 150 Aktien, 150 Bargeld, und wenn die Aktie um 1 Dollar fällt, dann ist der Marktwert der Aktie nur 75, aber Ihr Gesamtvermögen beträgt 225!

Wenn die Aktien fallen und dann wieder hochkommen, dann ist es das Gleiche, und Sie haben 25 Dollar verdient!

Das klingt nicht so realistisch, die Aktien haben sich verdoppelt, und der Rückgang ist nur ein halber Rückgang: 2 × 0,5-1 = 0, so oder so, aber der Kurs ist zurückgegangen, und Chansons Strategie hat tatsächlich Geld verdient.

Das Geheimnis des Geldes von Shannon liegt in der Verwendung der Kelly-Formel, der stärksten Gabel im Universum.

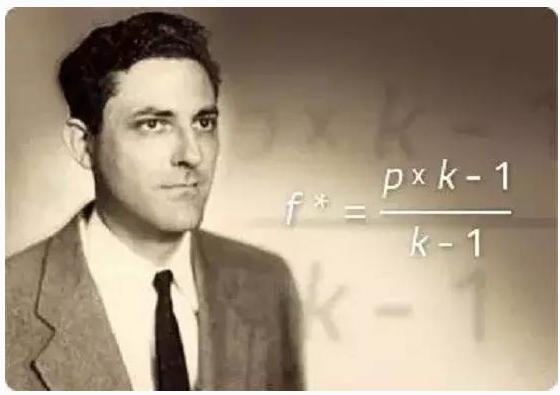
Die Formel wurde von Kelley, einem Kollegen von Shannon am Bell Laboratories, in die Anwendung von Kommunikationssignalen auf Basis von Shannons Informatik eingeführt.

Die Kelly-Formel, die in der Anlagewelt unter dem Namen “The Kelly-Wealth-Formula” bekannt ist, befasst sich mit der Frage, wie man den optimalen Anteil der Investitionen in einem Glücksspiel oder einer Investition anhand der Wahrscheinlichkeit der Verluste berechnet.

Die allgemeine Formel für die Kelly-Formel lautet: f=(pb-q) /b

P ist die Wahrscheinlichkeit, dass du Geld gewinnst (z.B. positiv), q ist natürlich die Wahrscheinlichkeit, dass du Geld verlierst, in einem Münzwurf sind diese beiden Werte 0,5 und b ist was? b ist deine Gewinnwahrscheinlichkeit, also wie viel Geld du noch gewinnen kannst, wenn du dein Geld verlierst.

Wenn du z.B. jedes Mal, wenn du 1 Münze spielst, 6 Münzen aus dem Haus bekommst, dann ist b gleich 5… 6 Münzen minus 1 Münze deines Geldes. In diesem Fall ist dein Geld pro Wette f=… 5×0.5-0.5)/5=40%, und in diesem Spiel, bei dem du 40 Prozent jedes Geldes spielst, ist deine Geometrie die höchste Erwartungshöhe für die zukünftige Rendite!

Es gibt keine bessere Investitionsquote-Anordnung als die Kelly-Formel!

Das Prinzip der Kelly-Formel ist eigentlich sehr einfach, wenn man den zukünftigen Gesamtwert eines Vermögens betrachtet:*(1-fa) ^ Nq (f: Investitionsanteil, b Gewinnwahrscheinlichkeit, a Verlustwahrscheinlichkeit, Np: Anzahl der Gewinne, Nq: Anzahl der Verluste), mit C f als Variable, um die beste f zu erhalten, ist die Formel: f = p/a-q/b

Diese Formel sieht anders aus als die vorher erwähnte f=(pb-q) / b, die eigentlich die gleiche ist, wenn du beim Verlieren alles verlierst ((z.B. wenn du eine Münze auf die richtige Seite wirfst, und wenn sie auf die falsche Seite kommt, hast du 1 Dollar verloren) dann ist a gleich 0, und wenn a gleich 0 ist, dann ist es die gleiche Formel wie zuvor.

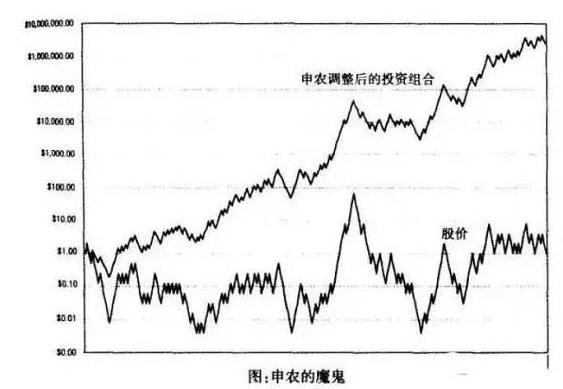
Wenn Sie die Kelly-Formel verwenden, um Shannon’s Devils noch einmal zu untersuchen, verdoppeln Sie, wenn Sie aufsteigen, was einem Einsatz entspricht, wenn Sie gewinnen, gibt Ihnen der Hausbesitzer zwei, wenn Sie fallen, halbieren Sie, was einem Einsatz entspricht, verlieren Sie und der Hausbesitzer verliert fünf Cents. Basierend auf diesen Informationen kann die Kelly-Formel verwendet werden, um die beste Position für Shannon’s Devils zu berechnen: f = p / a-q / b = 0,5 / 0,5 - 0,5 / 1 = 0,5

Das ist das Geheimnis von Shannon’s Devils, die Kelly-Formel berechnet, dass die optimale Investitionsquote die Hälfte des Kapitals ist, weshalb Shannon jedes Mal die gleiche Anpassung an den Marktwert benötigt.

Wie viel Geld verdient Shannon, wenn er diese Strategie durchführt?

Der oben beschriebene Prozess, der aus der Kelly-Formel abgeleitet wird, ergibt: C = 1 + 0,5 × 1) ^ Np*(1-0.5 × 0.5) ^ Nq, unter der Annahme, dass die Wahrscheinlichkeit von Auf- und Abwärtsbewegungen in der langen Zeitspanne gleich ist, ist Np = Nq = n, was bedeutet, dass:

In anderen Worten, wenn Shannon’s Vermögenswerte um die n-teine von 1,125 erhöht werden, klingt das nicht nach einem furchtbaren Gewinn?

Aber das widerspricht der Intuition, nicht wahr?

Stürzt auf, stürzt ab, stürzt auf, stürzt auf, stürzt auf, stürzt auf, stürzt hin und her, tritt hin und her, gibt Geld zurück?

Wenn wir das genauer untersuchen, finden wir eine Lücke: Wenn man bei einem Gewinn 1 Pfund investiert, verliert man bei einem Rückgang 1 Pfund, und wenn man bei einem Rückgang 1 Pfund investiert, verliert man nur 0,5. Wenn man die Wahrscheinlichkeitserwartungen berechnet: 1 × 0,5-0,5 × 0,5 = 0,25, dann gibt es eindeutig ein positives erwartetes Ergebnis.

Aber wenn es ein Spiel mit positiven Erwartungen gibt, warum sollte man dann, wenn man den ganzen Betrag hat, am Ende leer bleiben und keinen Cent verdienen?

Das ist ein sehr interessantes Phänomen, und es gibt eine sehr wichtige Beziehung zwischen Ihrem endgültigen Gewinn und Ihrer Position!

Wenn man sich in einem Spiel mit positiven Erwartungen auf ein gutes Ergebnis versetzt, kann man auch keinen Cent mehr verdienen.

Wenn wir den Teufel von Shannon mit dem Konzept des Profits messen, dann wird dieser Profit so aussehen: 2x0.5=1 (2: Verdoppelung, 0.5: Ausgleich), also ein Spiel, in dem es niemals einen Profit gibt, ein Spiel, in dem es niemals einen Profit gibt.

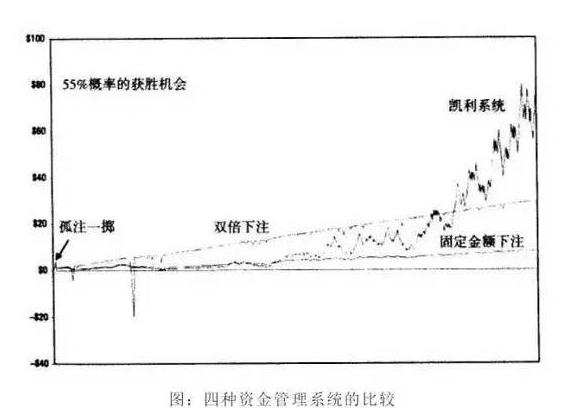
Die Kelly-Formel ist eine magische Formel, die die geometrische Rate der Rendite auf Null bringt, aber unendliche Reichtümer schafft.

Wenn wir uns die Dämonen von Shannon genauer anschauen, dann denken wir vielleicht, dass nach dem Anstieg und Fall alles wieder null ist und man noch Geld verdienen kann.

In der Realität ist es vielleicht die Illusion, dass die Wahrscheinlichkeit, dass ein Double weniger ist als die Wahrscheinlichkeit, dass ein Double weniger ist als die Wahrscheinlichkeit, dass ein Double weniger ist als die Wahrscheinlichkeit, dass ein Double weniger ist als eine Hälfte.

Und Shannon’s Devil impliziert, dass die Wahrscheinlichkeiten gleich sind. Ist es nicht absurd, wenn man so denkt, dass es vernünftig ist, dass die Wahrscheinlichkeiten unterschiedlich sind, dass es sonst aus dem Nichts Geld gibt?

Wir werden also jetzt untersuchen, ob die Wahrscheinlichkeit, dass ein Doppel steigt, dasselbe ist wie die Wahrscheinlichkeit, dass ein halber sinkt.

Einer ist um 100% gestiegen, der andere um 50%, und es sieht ganz anders aus, als wenn die Zahl, die um 100% gestiegen ist, kleiner ist als die Zahl, die um 50% gesunken ist.

Und langsam, 100% und 50% ist nur eine Bandbreite, nicht eine Wahrscheinlichkeit, was die Rendite der Börse, die akademische und die praktische Anwendung betrifft, ist die logarithmische Rendite, obwohl die Praxis zeigt, dass die logarithmische Rendite nicht perfekt in der normalen Verteilung ist, aber die Annäherung ist sehr hoch.

Bis wir ein besseres Modell haben, können wir uns die Erträge von Zahlenpaaren mit einer normalen Verteilung ansehen und direkt auf die Antwort kommen: Die logarithmische Rendite von 100% nach oben = ln(²⁄₁) = 0,6931, die logarithmische Rendite von 50% nach unten = ln(²⁄₁) = 0,6931, die Wahrscheinlichkeit für eine logarithmische Rendite von 100% nach oben und 50% nach unten ist in der logarithmischen Rendite normal verteilt!

In einem Gleichgewichtsszenario mit einer langfristigen Rendite von Null kann man mit Shannon’s Dämonen Geld verdienen.

Wie viel Geld verdient man mit 50 Bargeld und 50 Positionen?

Die logarithmische Rendite ist gleich der logarithmischen Rendite für die gleichen Zahlen: e^{\displaystyle e^{\displaystyle e^{\mathrm {e}}} -0.0953) = 0.909 ≠ 0.09531. Das heißt, dass die Wahrscheinlichkeit, dass wir sagen, dass die Wahrscheinlichkeit um 10% sinkt, ist: -9.09%.

Mit der Kelly-Formel berechnen wir die optimale Haltungsquote, und dann müssen wir in Zukunft nur noch mit Shannon’s teuflischen Aktien handeln, etwas verkaufen, etwas kaufen, eine feste Haltungsquote beibehalten, und dann können wir Shannon’s teuflische Gewinne erzielen!

Nach der vorherigen Kelly-Formel: f = p/a-q/b, bringen wir die Wahrscheinlichkeit und die Wahrscheinlichkeit, die wir gerade berechnet haben: f = 0.⁵⁄₀.0909-0.⁵⁄₀.1 = 5.5005-5 = 0.5005, ist fast gleich 0,5 .

Die optimale Haltungsquote, die nach der Kelly-Formel berechnet wird, beträgt also 50 Prozent der Positionen (wenn man 10 Prozent in 30 Prozent umwandelt, wird die Haltungsquote zu 200 Prozent, ein doppeltes Leverage).

Wie ich bereits in meinem Vortrag über die Kelly-Formel erwähnt habe:

C=（1+fb)^Np(1-fa) ^ Nq, wir setzen die Zahlen, die wir gerade berechnet haben, in: C=(1+0.5×0.1)(1-0.5×0.0909)^n=(1.05×0.95455)^n=1.0022^n

Eine Maschine, die nach der Kelly-Formel des perfekten Anlageverhältnisses entwickelt wurde und durch den perfekten Handel in einem Raum mit einer Vibration von 19,09% unter der Voraussetzung einer normalen Verteilung der logarithmischen Rendite der Aktienmärkte einen Nettogewinn von 0,22% pro Transaktion aus dem Markt erzielen kann, ohne die Transaktionskosten zu berücksichtigen.

Im Rahmen der Regeln ist diese Gewinnspanne die schnellste Wachstumsrate des Kontokapitals, was der Grundprinzip ist, dass der Gitterhandel mit Positionsmanagement profitabel ist, wenn 0 erwartet wird.

Zusammenfassend kann man sagen, dass die Gitter-Trading-Methode eine sehr gute Handelsmethode ist, aber es gibt auch einige Nachteile, wie die Möglichkeit, dass die Regeln nicht funktionieren, wie z. B. Angst vor einem Netzbruch, Angst vor einer einseitigen Seite usw.

Ein paar Tipps zum Umgang mit Gitter: Grid-Trading-Regeln detailliert Wissenschaftliche Prinzipien für einen stabilen Gewinn https://www.fmz.cn/bbs-topic/7568 Vor- und Nachteile von Gitterhandel und Strategien zur Optimierung Grid-Trading-Strategie-Optimierung - Wie man die richtige Investitionsart wählt Optimierung der Grid-Strategie - Einseitige Absenkung und Verringerung der Ausbruchrate Grid-Strategieoptimierung - Schnelle Lösungen für die Positionsverwaltung Die Grid-Trading-Legislative ist endgültig optimiert - die Gewinnspanne der Grid-Trading-Legislative kann um das Fünffache erhöht werden. Ein Netzwerk-Strategien, um die High-Frequency-Streaming-Strategie zu manipulieren