Neuronale Netzwerke und digitale Währung Quantitative Trading Series (1) - LSTM prognostiziert Bitcoin Preis
Schriftsteller:FMZ~Lydia, Erstellt: 2023-01-12 13:55:01, Aktualisiert: 2024-12-19 21:12:23
Neuronale Netzwerke und digitale Währung Quantitative Trading Series (1) - LSTM prognostiziert Bitcoin Preis
1. Kurze Einführung
Das tiefe neuronale Netzwerk ist in den letzten Jahren immer beliebter geworden. Es hat die Probleme gelöst, die in der Vergangenheit in vielen Bereichen nicht gelöst werden konnten, und hat seine starke Fähigkeit gezeigt. Bei der Vorhersage von Zeitreihen ist der häufig verwendete neuronale Netzwerkpreis RNN, da er nicht nur aktuelle Dateneingabe, sondern auch historische Dateneingabe hat. Natürlich, wenn wir über RNN-Preisvorhersage sprechen, sprechen wir oft über eines der RNNs: LSTM. Dieses Papier wird ein Modell für die Vorhersage des Bitcoin-Preises auf der Grundlage von PyTorch erstellen. Obwohl es viele relevante Informationen im Internet gibt, ist es immer noch nicht gründlich genug, und es gibt relativ wenige Leute, die PyTorch verwenden. Es ist immer noch notwendig, einen Artikel zu schreiben. Das Endergebnis ist die Verwendung des Eröffnungspreises, des Schließpreises, des höchsten Handelspreises, des niedrigsten Preises und des Volumens von Bitcoin, um den nächsten Schließ Dieses Tutorial wurde von der FMZ Quant Trading Plattform erstellt (www.fmz.com) Willkommen zur QQ-Gruppe: 863946592 für Kommunikation.
2. Daten und Referenzen
Bitcoin-Preisdaten stammen von der FMZ Quant Trading Plattform:https://www.quantinfo.com/Tools/View/4.html- Ich weiß. Ein verwandtes Beispiel für die Preisvorhersage:https://yq.aliyun.com/articles/538484- Ich weiß. Eine ausführliche Einführung in das RNN-Modell:https://zhuanlan.zhihu.com/p/27485750- Ich weiß. Verständnis der Eingaben und Ausgänge von RNN:https://www.zhihu.com/question/41949741/answer/318771336- Ich weiß. Über den Pytorch: die offizielle Dokumentation:https://pytorch.org/docsFür weitere Informationen können Sie selbst suchen. Darüber hinaus benötigen Sie einige Vorkenntnisse, um diesen Artikel zu lesen, wie z.B. Pandas/Python/Datenverarbeitung, aber es spielt keine Rolle, wenn Sie das nicht tun.
3. Parameter des Pytorch-LSTM-Modells
Parameter des LSTM:
Als ich das erste Mal diese dichten Parameter auf dem Dokument sah, war meine Reaktion: Was zum Teufel ist das?
Als ich langsam las, verstand ich es endlich.

input_size: Geben Sie die charakteristische Größe des Vektors x ein. Wenn der Schlusskurs durch den Schlusskurs vorhergesagt wird, dann input_size=1; Wenn der Schlusskurs durch hohe Öffnung und niedrige Schließung vorhergesagt wird, dann input_size=4.hidden_size: Implizite Schichtgrößenum_layers: Anzahl der Schichten der RNN.batch_first: Wenn wahr, ist die erste Eingabedimension batch_size, die ebenfalls sehr verwirrend ist und im Folgenden ausführlich beschrieben wird.
Eingabe der Datenparameter:
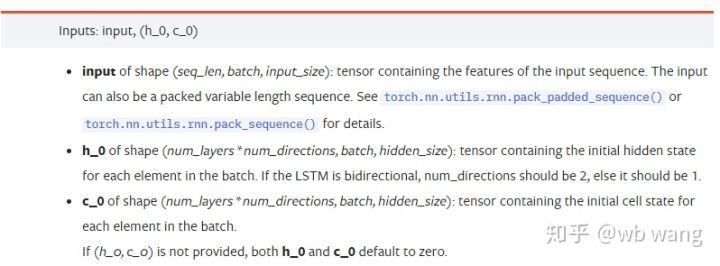
input: Die spezifischen Eingabedaten sind ein dreidimensionales Tensor, und die spezifische Form ist: (seq_len, batch, input_size). Wo sich seq_len auf die Länge der Sequenz bezieht, dh wie lange das LSTM die historischen Daten berücksichtigen muss. Beachten Sie, dass sich dies nur auf das Format der Daten bezieht, nicht auf die interne Struktur des LSTM. Das gleiche LSTM-Modell kann verschiedene seqs_lenh_0: Anfangs versteckter Zustand, Form als (num_layers * num_directions, batch, hidden_size), wenn es sich um ein zweiseitiges Netzwerk handelt, num_directions=2.c_0: Der Anfangszustand der Zelle, die Form wie oben, kann nicht angegeben werden.
Ausgangsparameter:
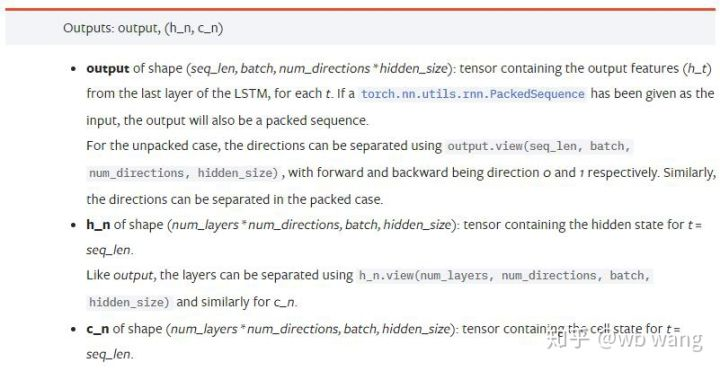
output: Die Form der Ausgabe (seq_len, batch, num_directions * hidden_size), beachten Sie, dass sie mit dem Modellparameter batch_first verknüpft ist.h_n: Der Zustand h zum Zeitpunkt von t = seq_len, gleiche Form wie h_0.c_n: Der z-Zustand zum Zeitpunkt von t = seq_len, gleiche Form wie c_0.
4. Ein einfaches Beispiel für LSTM-Eingabe und Ausgabe
Import des erforderlichen Pakets zuerst
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
Definition des LSTM-Modells
LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)
Bereiten Sie die Eingabedaten vor
x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657, 1.4398, -0.3479, 0.2685, 1.6903],
[ 1.0738, 0.6283, -1.3682, -0.1002, -1.7200],
[ 0.2836, 0.3013, -0.3373, -0.3271, 0.0375],
[-0.8852, 1.8098, -1.7099, -0.5992, -0.1143]],
[[ 0.6970, 0.6124, -0.1679, 0.8537, -0.1116],
[ 0.1997, -0.1041, -0.4871, 0.8724, 1.2750],
[ 1.9647, -0.3489, 0.7340, 1.3713, 0.3762],
[ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],
[[-0.5309, 0.1540, -0.4613, -0.6425, -0.1957],
[-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
[-0.4453, 0.1987, -1.0775, 1.3212, 1.3577],
[-0.5488, 0.6669, -0.2151, 0.9337, -1.1805]]])
Die Form von x ist (3,4,5), weil wir definiertbatch_first=Truezuvor, die Größe von batch_size zu diesem Zeitpunkt ist 3, sqe_len ist 4, input_size ist 5. X [0] repräsentiert die erste Charge.
Wenn batch_first nicht definiert ist, ist der Standardwert False, dann ist die Datendarstellung zu diesem Zeitpunkt völlig anders. Die Batchgröße ist 4, sqe_len ist 3, input_size ist 5. Zu diesem Zeitpunkt stellt x [0] die Daten aller Chargen dar, wenn t = 0, und so weiter. Ich habe das Gefühl, dass diese Einstellung nicht intuitiv ist, also habe ich den Parameter hinzugefügtbatch_first=True.
Die Datenumwandlung zwischen den beiden ist ebenfalls sehr praktisch:x.permute (1,0,2)
Eingang und Ausgang
Die Form der Eingabe und Ausgabe von LSTM ist sehr verwirrend, und die folgende Abbildung kann uns helfen zu verstehen:
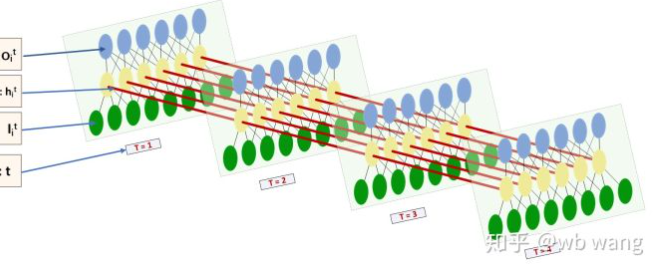
Von:https://www.zhihu.com/question/41949741/answer/318771336.
x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])
Beachten Sie, dass der zweite Wert von hn.size() 3 ist, was mit der Größe von batch_size übereinstimmt, was bedeutet, dass der Zwischenzustand nicht in hn gespeichert wird, sondern nur der letzte Schritt. Da unser LSTM-Netzwerk zwei Schichten hat, ist die Ausgabe der letzten Schicht von hn der Ausgabewert. Die Form der Ausgabe ist [3, 4, 10], die die Ergebnisse zu allen Zeiten von t = 0,1,2,3 speichert, also:
hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]
5. Bereiten Sie Bitcoin Marktdaten vor
Es ist sehr wichtig, die Eingabe und Ausgabe von LSTM zu verstehen. Andernfalls ist es leicht, Fehler zu machen, indem man zufällig einige Codes aus dem Internet extrahiert. Aufgrund der starken Fähigkeit von LSTM in Zeitreihen, auch wenn das Modell falsch ist, können am Ende gute Ergebnisse erzielt werden.
Datenerfassung
Die Marktdaten des Handelspares BTC_USD in der Bitfinex Exchange werden verwendet.
import requests
import json
resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))
Das Datenformat ist wie folgt:
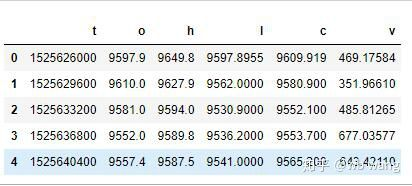
Datenvorverarbeitung
df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.
Die Methode der Datenstandardisierung ist sehr grob, und es wird einige Probleme geben.
Bereitstellung von Ausbildungsdaten
seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
dataX, dataY=[], []
for i in range(0,len(data)-seq_len, seq_len):
dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
dataY.append(data['n'][i:i+seq_len].values)
return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))
Die endgültigen Formen von train_x und train_y sind: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). Da unser Modell den Schlusskurs der nächsten Periode basierend auf den Daten von 10 Perioden vorhersagt, gibt es theoretisch 800 Chargen, solange es 800 vorhergesagte Schlusskosten gibt. Aber train_y in jeder Charge hat 10 Daten. Tatsächlich ist das Zwischenergebnis jeder Chargenvorhersage reserviert. Bei der Berechnung des Endverlusts können alle 10 Vorhersageergebnisse berücksichtigt und mit dem tatsächlichen Wert in train_y verglichen werden. Theoretisch können wir den Verlust nur des letzten Vorhersageergebnisses berechnen. Da das LSTM-Modell den Seq_lenful-Parameter nicht enthält, kann das Modell auf verschiedene Längen angewendet werden, und die Vorhersageergebnisse in der Mitte sind auch sinnvoll, daher ziehe ich es vor, Verlust zu kombinieren und zu berechnen.
Beachten Sie, dass bei der Vorbereitung von Trainingsdaten die Bewegung des Fensters springt, und die bereits verwendeten Daten werden nicht mehr verwendet. Natürlich kann das Fenster auch einzeln verschoben werden, so dass das erhaltene Trainingsset viel größer ist. Allerdings fand ich, dass die angrenzenden Chargendaten zu sich wiederholend waren, also habe ich die aktuelle Methode übernommen.
6. Erstellen des LSTM-Modells
Das endgültige Modell ist wie folgt konstruiert und enthält eine zweischichtige LSTM und eine lineare Schicht.
class LSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
super(LSTM, self).__init__()
self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.
def forward(self, x):
x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
x = self.reg(x)
return x
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.
7. Beginnen Sie mit der Ausbildung des Modells
Schließlich beginnen wir mit dem Training. Der Code lautet:
criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
loss = criterion(out, train_y)
optimizer.zero_grad()
loss.backward() # Reverse propagation losses
optimizer.step() # Update parameters
print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))
Die Ergebnisse der Ausbildung sind wie folgt:
8. Modellbewertung
Vorhersagter Wert des Modells:
p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()
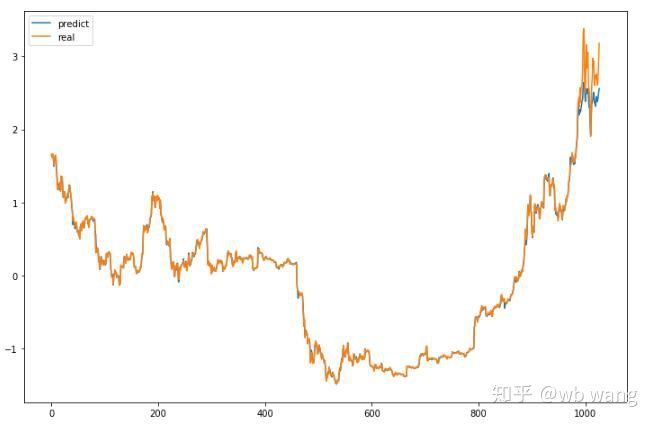
Aus dem Diagramm ist zu sehen, dass die Trainingsdaten (vor 800) sehr konsistent sind, aber der Preis von Bitcoin ist in der späteren Periode gestiegen. Obwohl der vorhergesagte Preis möglicherweise nicht genau ist, wie genau ist die Vorhersage des steigenden und sinkenden Preises?
r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))
Ich möchte jedoch sagen, daß die Kommission nicht bereit ist, eine Reihe von Änderungsanträgen zu unterbreiten.
Natürlich ist dieses Modell nicht auf den echten Bot anwendbar, aber es ist einfach und leicht zu verstehen.
- Einführung in Lead-Lag-Arbitrage in Kryptowährungen (2)
- Einführung der Lead-Lag-Suite in der digitalen Währung (2)
- Diskussion über den externen Signalempfang der FMZ-Plattform: Eine Komplettlösung für den Empfang von Signalen mit integriertem Http-Service in der Strategie
- FMZ-Plattform: Erforschung von Signalempfangsstrategien für externe Netzwerke
- Einführung in Lead-Lag-Arbitrage in Kryptowährungen (1)
- Einführung der Lead-Lag-Suite in der Kryptowährung (1)
- Diskussion über den externen Signalempfang der FMZ-Plattform: Erweiterte API VS Strategie eingebauter HTTP-Service
- FMZ-Plattform-External Signal Reception: Erweiterung der API vs. Strategien für den eingebauten HTTP-Dienst
- Diskussion über die Strategie-Testmethode auf Basis eines Zufalls-Ticker-Generators
- Strategie-Testmethoden basierend auf Random-Market-Generatoren untersucht
- Neue Funktion von FMZ Quant: _Serve-Funktion zum einfachen Erstellen von HTTP-Diensten
- Pivot Point Intraday Trading System (Einzelhandelssystem für den Intraday-Handel)
- 6 einfache Strategien und Praktiken für Anfänger im quantitativen Handel mit digitaler Währung
- Strategischer Rahmen für den realen Durchschnittsbereich
- Praxis und Anwendung der Thermostatstrategie auf der FMZ Quant-Plattform
- Handelsstrategie auf der Grundlage der Box-Theorie zur Unterstützung von Rohstofffutures und digitaler Währung
- Relative Stärke Quantitative Handelsstrategie auf Basis des Preises
- Quantitative Handelsstrategie mit einem gewichteten Handelsvolumenindex
- Umsetzung und Anwendung der PBX-Handelsstrategie auf der FMZ Quant Trading-Plattform
- Spätes Teilen: Bitcoin-Hochfrequenz-Roboter mit täglicher Rendite von 5% im Jahr 2014
- Neuronale Netzwerke und Quantitative Trading in digitaler Währung (2) - Intensives Lernen und Schulen Bitcoin Trading Strategie
- Anwendung der Kombinationsstrategie von SMA und RSI Relative Strength Index
- Entwicklung der CTA-Strategie und der Standardklassenbibliothek der FMZ Quant-Plattform
- Quantitative Handelsstrategie mit Preisdynamikanalyse in Python
- Implementieren Sie eine Dual-Push-Quantitative Trading-Strategie für digitale Währungen in Python
- Der beste Weg zum Installieren und Upgrade für Linux Docker
- Erreichung einer ausgewogenen Eigenkapitalstrategie mit einer ordnungsgemäßen Ausrichtung von Long-Short-Positionen
- Zeitreihendatenanalyse und Tick-Daten-Backtesting
- Quantitative Analyse des Marktes für digitale Währungen
- Paarhandel auf Basis datengetriebener Technologie
- Anwendung der Maschinellen Lerntechnologie im Handel