En el artículo anterior (https://www.fmz.com/digest-topic/4187), presentamos estrategias de trading de pares y demostramos cómo utilizar datos y análisis matemático para crear y automatizar estrategias de trading.

La estrategia de renta variable equilibrada de largo-corto plazo es una extensión natural de la estrategia de negociación de pares aplicable a una canasta de objetivos comerciales. Es especialmente adecuado para operar en mercados con muchas variedades e interrelaciones, como el mercado de divisas digitales y el mercado de futuros de materias primas.

Principios básicos

La estrategia de renta variable equilibrada a largo y corto plazo consiste en invertir en largo y corto plazo en una canasta de objetivos comerciales al mismo tiempo. Al igual que en el trading de pares, determine qué objetivos de inversión son baratos y cuáles son caros. La diferencia es que la estrategia de acciones equilibrada a largo plazo y a corto plazo clasificará todos los objetivos de inversión en un grupo de selección de acciones para determinar qué objetivos de inversión son relativamente baratos o caros. Luego, se posicionará en largo en las n inversiones principales según la clasificación, y en corto en las n inversiones inferiores con una cantidad igual (valor total de las posiciones largas = valor total de las posiciones cortas).

¿Recuerdas cuando dijimos anteriormente que el trading de pares es una estrategia neutral en el mercado? Lo mismo se aplica a una estrategia de renta variable equilibrada a largo y corto plazo, ya que la misma cantidad de posiciones largas y cortas garantiza que la estrategia permanecerá neutral en el mercado (no se verá afectada por las fluctuaciones del mercado). La estrategia también es estadísticamente sólida: al clasificar las inversiones y tomar múltiples posiciones, puede exponer su modelo de clasificación a múltiples exposiciones, en lugar de solo una exposición de riesgo única. Lo único en lo que estás apostando es en la calidad de tu sistema de clasificación.

¿Qué es un sistema de clasificación?

Un esquema de clasificación es un modelo que asigna una prioridad a cada objetivo de inversión en función de su rendimiento esperado. Los factores pueden ser factores de valor, indicadores técnicos, modelos de precios o una combinación de todos los anteriores. Por ejemplo, podría utilizar la métrica de impulso para clasificar una lista de inversiones que siguen tendencias: se esperaría que las inversiones con el mayor impulso sigan teniendo un buen desempeño y reciban las clasificaciones más altas; las inversiones con el menor impulso tendrán el peor desempeño y tienen los rendimientos más bajos.

El éxito de esta estrategia depende casi por completo del esquema de clasificación utilizado, es decir, su esquema de clasificación es capaz de separar las inversiones de alto rendimiento de las de bajo rendimiento, obteniendo mejor los retornos de la estrategia objetivo de inversión a largo-corto plazo. Por lo tanto, es muy importante desarrollar un esquema de clasificación.

¿Cómo formular un plan de ranking?

Una vez que tengamos un sistema de clasificación establecido, obviamente queremos poder sacar provecho de él. Logramos esto invirtiendo la misma cantidad de dinero para comprar las inversiones de mayor rango y vender las de menor rango. Esto garantiza que la estrategia sólo ganará dinero en proporción a la calidad de sus clasificaciones y será “neutral al mercado”.

Supongamos que está clasificando todas las inversiones m, tiene n dólares para invertir y desea mantener un total de 2p (donde m>2p) posiciones. Si se espera que la inversión con rango 1 tenga el peor desempeño, entonces se espera que la inversión con rango m tenga el mejor desempeño:

• Organiza los objetivos de inversión de la siguiente manera: 1, …, p y objetivos de inversión cortos en USD 2/2p

• Organiza los objetivos de inversión como: m-p,……,m, y entra en largo en n/2p dólares de objetivos de inversión.

Aviso:Dado que el precio objetivo debido a los saltos de precios no siempre dividirá n/2p de manera uniforme, y algunos objetivos deben comprarse en números enteros, habrá algunos algoritmos inexactos, y el algoritmo debe ser lo más cercano posible a este número. Para la estrategia ejecutada con n = 100000 y p = 500, vemos:

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

Esto puede causar grandes problemas para precios con fracciones mayores a 100 (como los mercados de futuros de materias primas), porque no se pueden abrir posiciones con precios fraccionarios (este problema no existe en el mercado de criptomonedas). Mitigamos esto reduciendo las transacciones a precios fraccionados o aumentando el capital.

Veamos un ejemplo hipotético.

• Desarrollamos nuestro entorno de investigación en la plataforma cuantitativa Inventor

En primer lugar, para que funcione sin problemas, necesitamos crear nuestro entorno de investigación. En este artículo, utilizamos Inventor Quantitative Platform (FMZ.COM) para crear el entorno de investigación, principalmente para que podamos utilizar la API rápida y conveniente. Interfaz y encapsulamiento de esta plataforma posteriormente. Sistema Docker completo.

En el nombre oficial de Inventor Quantitative Platform, este sistema Docker se denomina sistema host.

Para obtener más información sobre cómo implementar hosts y robots, consulte mi artículo anterior: https://www.fmz.com/bbs-topic/4140

Los lectores que quieran comprar su propio servidor de implementación de computación en la nube pueden consultar este artículo: https://www.fmz.com/bbs-topic/2848

Después de implementar con éxito el servicio de computación en la nube y el sistema host, instalaremos la herramienta Python más poderosa: Anaconda

Para lograr todos los entornos de programa relevantes necesarios para este artículo (bibliotecas dependientes, gestión de versiones, etc.), la forma más sencilla es utilizar Anaconda. Es un ecosistema de ciencia de datos Python empaquetado y un administrador de dependencias.

Para conocer el método de instalación de Anaconda, consulte la guía oficial de Anaconda: https://www.anaconda.com/distribution/

Este artículo también utilizará numpy y pandas, dos bibliotecas muy populares e importantes en la computación científica de Python.

Para el trabajo básico mencionado anteriormente, también puede consultar mi artículo anterior, que presenta cómo configurar el entorno de Anaconda y las dos bibliotecas numpy y pandas. Para obtener más detalles, consulte: https://www.fmz.com/digest- tema/4169

Generamos inversiones aleatorias y factores aleatorios y los clasificamos. Supongamos que nuestros rendimientos futuros realmente dependen de los valores de estos factores.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

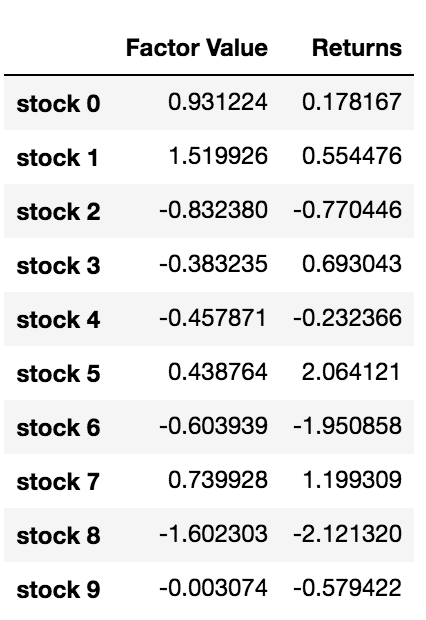
Ahora que tenemos los valores de los factores y los rendimientos, podemos ver qué sucede si clasificamos las inversiones en función de los valores de los factores y luego abrimos posiciones largas y cortas.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

Nuestra estrategia es posicionarnos a largo plazo en la inversión mejor clasificada de una canasta de objetivos de inversión y a corto plazo en la inversión mejor clasificada de un objetivo. Las recompensas de esta estrategia son:

basket_returns[number_of_baskets-1] - basket_returns[0]

El resultado es: 4,172

Invierta su dinero en nuestro modelo de clasificación para separar las inversiones de alto rendimiento de las de bajo rendimiento.

En el resto de este artículo, analizamos cómo evaluar esquemas de clasificación. El beneficio de ganar dinero con el arbitraje basado en clasificación es que no se ve afectado por el desorden del mercado, sino que puede aprovecharlo.

Consideremos un ejemplo del mundo real.

Cargamos datos de 32 acciones de diferentes sectores del S&P 500 y tratamos de clasificarlas.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Utilicemos el indicador de impulso normalizado durante un período de un mes como base para la clasificación.

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Ahora analizaremos el comportamiento de nuestras acciones y veremos cómo se comportan nuestras acciones en el mercado dentro de los factores de ranking que hemos elegido.

Analizar los datos

Comportamiento de las acciones

Echemos un vistazo a cómo se comporta nuestra canasta de acciones seleccionada en nuestro modelo de clasificación. Para ello, calculemos los rendimientos futuros de una semana para todas las acciones. Luego podemos observar la correlación del rendimiento futuro de una semana de cada acción con el impulso de los 30 días anteriores. Las acciones que muestran una correlación positiva siguen la tendencia, y las acciones que muestran una correlación negativa revierten la media.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

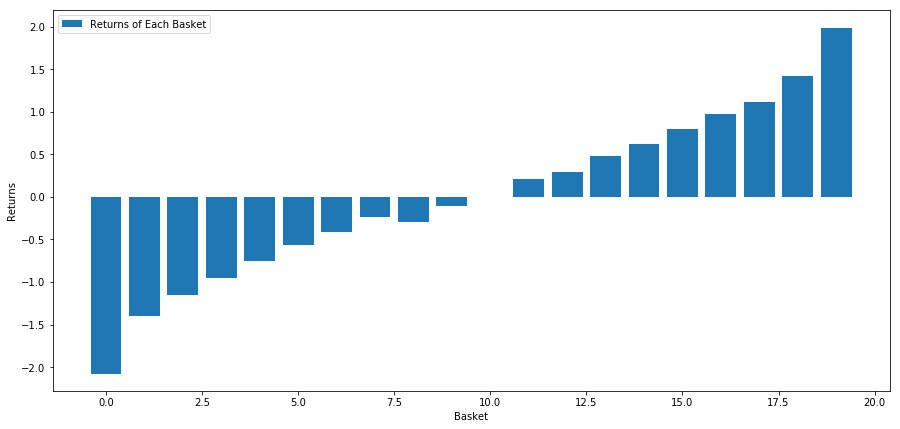
¡Todas nuestras acciones tienen una reversión a la media en algún grado! (Aparentemente nuestro universo elegido funciona de esta manera) Esto nos dice que si una acción tiene una alta calificación en el análisis de impulso, deberíamos esperar que tenga un rendimiento inferior la próxima semana.

Correlación entre la clasificación de la puntuación de momentum y los retornos

A continuación, debemos analizar la correlación entre nuestra puntuación de clasificación y los rendimientos futuros generales del mercado, es decir, la relación entre la predicción de los rendimientos esperados y nuestros factores de clasificación. ¿Pueden los niveles de correlación más altos predecir rendimientos relativos más bajos, o viceversa?

Para ello, calculamos la correlación diaria entre el impulso de 30 días y los retornos futuros de 1 semana para todas las acciones.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

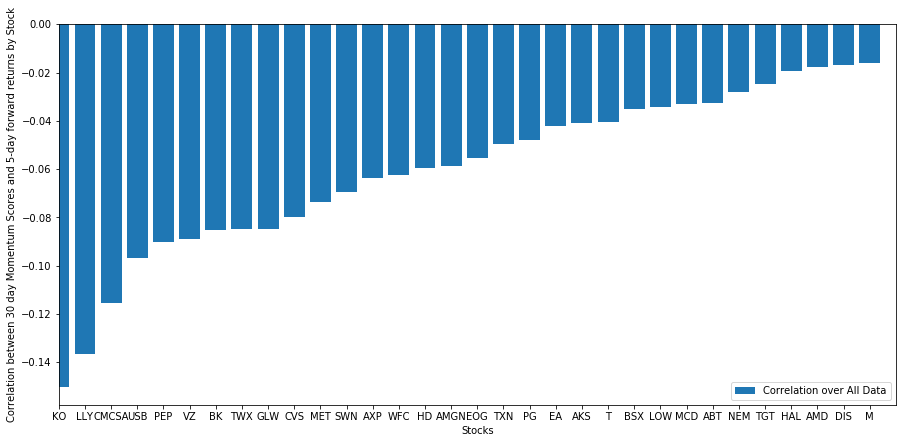
La correlación diaria es bastante ruidosa, pero muy leve (lo cual es de esperarse ya que dijimos que todas las acciones revertirán a la media). También observamos la correlación mensual promedio de los rendimientos futuros de 1 mes.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

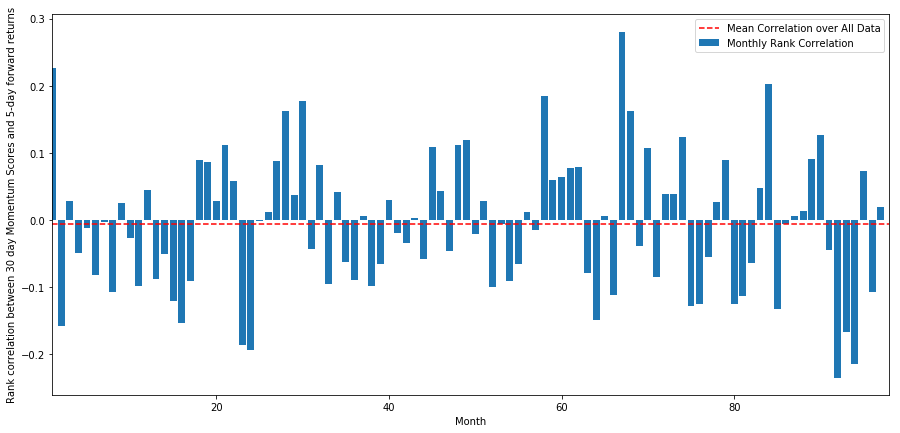
Podemos ver que la correlación promedio es nuevamente ligeramente negativa, pero también varía mucho de mes a mes.

Rendimiento promedio de la cesta de acciones

Hemos calculado la rentabilidad de una cesta de acciones extraídas de nuestro ranking. Si clasificamos todas las acciones y luego las dividimos en n grupos, ¿cuál será el rendimiento promedio de cada grupo?

El primer paso es crear una función que proporcione el rendimiento promedio y el factor de clasificación para cada canasta entregada cada mes.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Calculamos el rendimiento promedio de cada canasta al clasificar las acciones en función de esta puntuación. Esto debería darnos una buena idea de su relación a lo largo de un largo período de tiempo.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

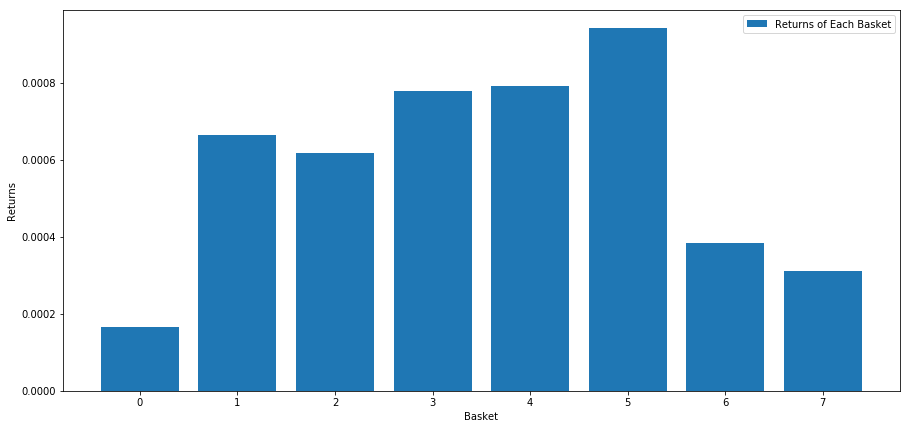
Parece que somos capaces de separar a los de alto rendimiento de los de bajo rendimiento.

Consistencia de la pasta (base)

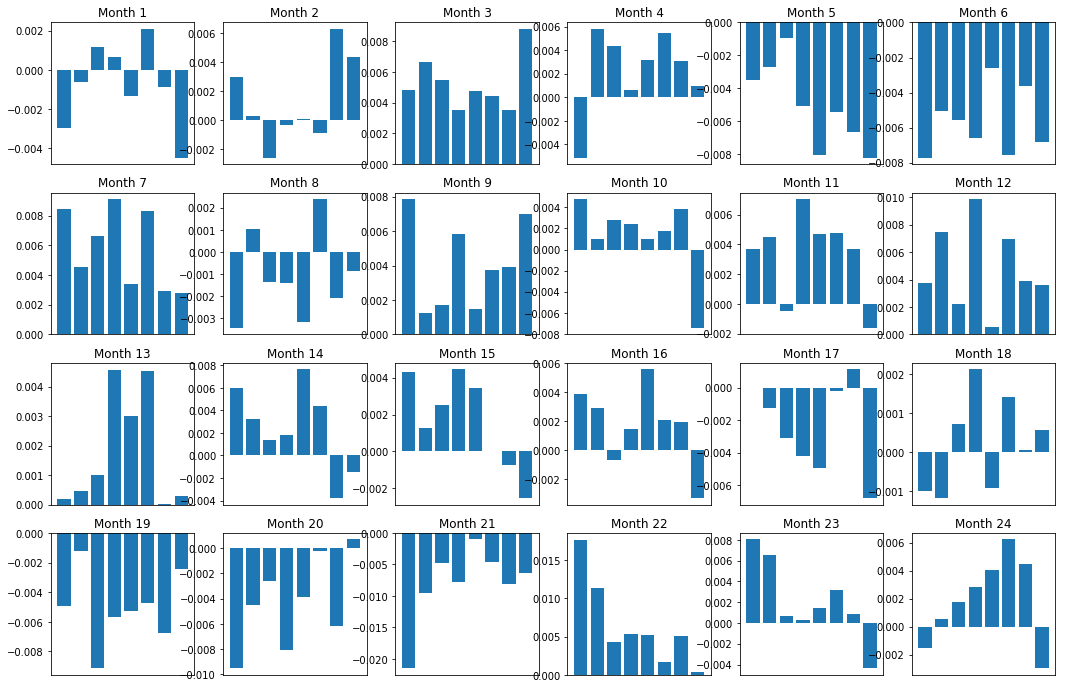
Por supuesto, estas son sólo relaciones promedio. Para entender qué tan consistente es la relación y si estamos dispuestos a llegar a un acuerdo, debemos cambiar nuestro enfoque y actitud hacia ella con el tiempo. A continuación, analizaremos sus diferenciales mensuales (base) de los dos años anteriores. Podemos ver más cambios y realizar análisis adicionales para determinar si esta puntuación de impulso es negociable.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

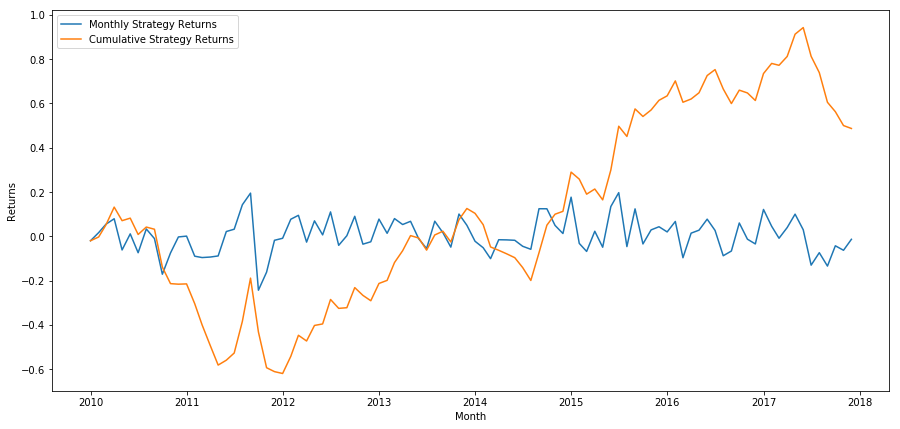
Por último, veamos los retornos si tuviéramos una posición larga en la última canasta y una posición corta en la primera canasta cada mes (suponiendo una asignación de capital igual a cada valor).

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Rentabilidad anual: 5,03%

Vemos que tenemos un sistema de clasificación muy débil que sólo distingue modestamente las acciones de alto rendimiento de las de bajo rendimiento. Además, no existe consistencia en este esquema de clasificación y varía ampliamente de un mes a otro.

Encontrar el sistema de clasificación adecuado

Para implementar una estrategia de renta variable equilibrada a largo y corto plazo, en realidad sólo es necesario determinar el esquema de clasificación. Todo lo que viene después es mecánico. Una vez que tenga una estrategia de acciones equilibrada a largo y corto plazo, puede intercambiar diferentes factores de clasificación sin cambiar mucho más. Esta es una forma muy conveniente de iterar rápidamente sus ideas sin tener que preocuparse por modificar todo el código cada vez.

El esquema de clasificación también puede provenir de casi cualquier modelo. No tiene por qué ser un modelo factorial basado en valores, podría ser una técnica de aprendizaje automático que prediga los retornos con un mes de anticipación y los clasifique en función de eso.

Selección y evaluación de sistemas de clasificación

El esquema de clasificación es la ventaja de la estrategia de renta variable equilibrada largo-corto y también es el componente más importante. Elegir un buen esquema de clasificación es un proyecto sistemático y no hay respuestas sencillas.

Un buen punto de partida es elegir tecnologías conocidas existentes y ver si se pueden modificar ligeramente para obtener mayores rendimientos. Discutiremos aquí algunos puntos de partida:

• Clonar y ajustarElige algo que se discuta a menudo y ve si puedes modificarlo ligeramente para tu beneficio. Por lo general, los factores públicos ya no tendrán señales comerciales porque han sido completamente arbitrados fuera del mercado. Sin embargo, a veces pueden guiarte en la dirección correcta.

• Modelo de precios:Cualquier modelo que prediga retornos futuros puede ser un factor y tiene el potencial de ser utilizado para clasificar su canasta de objetivos comerciales. Puede tomar cualquier modelo de precios complejo y convertirlo en un esquema de clasificación.

• Factores basados ​​en el precio (indicadores técnicos)Los factores basados ​​en el precio, como los que hemos analizado hoy, toman información sobre el precio histórico de cada acción y la utilizan para generar un valor de factor. Algunos ejemplos podrían ser indicadores de media móvil, indicadores de impulso o indicadores de volatilidad.

• Regresión y momentum:Cabe señalar que algunos factores creen que una vez que los precios se mueven en una dirección, continuarán haciéndolo. Algunos factores son exactamente lo opuesto. Ambos son modelos válidos en diferentes marcos temporales y activos, y es importante estudiar si el comportamiento subyacente se basa en el impulso o en la regresión.

• Factores fundamentales (basados ​​en valores):Esto utiliza una combinación de valores fundamentales como PE, dividendos, etc. El valor fundamental contiene información relacionada con hechos reales sobre una empresa y, por lo tanto, puede ser más poderoso que el precio en muchos sentidos.

En última instancia, desarrollar predictores es una carrera armamentista en la que se intenta estar un paso adelante. Los factores se arbitran fuera del mercado y tienen una vida útil, por lo que debe realizar continuamente el trabajo para determinar cuánto deterioro han experimentado sus factores y qué factores nuevos se pueden usar para reemplazarlos.

Otras consideraciones

• Frecuencia de reequilibrio

Cada sistema de clasificación predice rendimientos en un período de tiempo ligeramente diferente. La reversión a la media basada en precios podría ser predictiva durante unos pocos días, mientras que los modelos factoriales basados ​​en valores podrían ser predictivos durante unos pocos meses. Es muy importante determinar el horizonte temporal que el modelo debe pronosticar y validarlo estadísticamente antes de ejecutar la estrategia. Ciertamente, no conviene sobreajustar intentando optimizar la frecuencia de reequilibrio; inevitablemente, encontrará uno que supere aleatoriamente a los demás. Una vez que haya determinado el horizonte temporal que predice su esquema de clasificación, intente reequilibrar aproximadamente con esa frecuencia para Saca el máximo partido a tu modelo.

• Capacidad de capital y costos de transacción

Cada estrategia tiene un requisito de capital mínimo y máximo; el umbral mínimo suele estar determinado por los costos de transacción.

Operar con demasiadas acciones dará como resultado costos de transacción elevados. Suponiendo que desea comprar 1.000 acciones, cada reequilibrio supondrá unos costes de varios miles de dólares. Su base de capital debe ser lo suficientemente alta como para que los costos de transacción representen una pequeña fracción de los rendimientos generados por su estrategia. Por ejemplo, si su capital es de \(100,000 y su estrategia gana 1% (\)1000) por mes, todo ese retorno será consumido por los costos de transacción. Necesitarías millones de dólares de capital para ejecutar esta estrategia y obtener ganancias en más de 1.000 acciones.

El umbral mínimo de activos depende principalmente del número de acciones negociadas. Sin embargo, la capacidad máxima también es muy alta, y las estrategias de acciones equilibradas a largo y corto plazo pueden negociar cientos de millones de dólares sin perder su ventaja. Esto es así porque la estrategia se reequilibra con relativa poca frecuencia. El monto total de activos dividido por la cantidad de acciones negociadas dará como resultado un valor en dólares por acción muy bajo, y usted no tiene que preocuparse de que su volumen de operaciones mueva el mercado. Digamos que usted negocia 1.000 acciones, eso equivale a 100.000.000 de dólares. Si reequilibrara su cartera completa cada mes, solo negociaría $100,000 por mes por acción, lo que no es suficiente para representar una participación de mercado significativa para la mayoría de los valores.