Las redes neuronales y la serie de comercio cuantitativo de moneda digital (1) - LSTM predice el precio de Bitcoin
El autor:FMZ~Lydia, Creado: 2023-01-12 13:55:01, Actualizado: 2024-12-19 21:12:23
Las redes neuronales y la serie de comercio cuantitativo de moneda digital (1) - LSTM predice el precio de Bitcoin
1. Breve introducción
La red neuronal profunda se ha vuelto cada vez más popular en los últimos años. Ha resuelto los problemas que no se podían resolver en el pasado en muchos campos y ha demostrado su fuerte capacidad. En la predicción de series temporales, el precio de la red neuronal comúnmente utilizado es RNN, porque no solo tiene entrada de datos actual, sino también entrada de datos históricos. Por supuesto, cuando hablamos de predicción de precios de RNN, a menudo hablamos de uno de los RNN: LSTM. Este artículo construirá un modelo para predecir el precio de Bitcoin basado en PyTorch. Aunque hay mucha información relevante en Internet, todavía no es lo suficientemente completa, y hay relativamente pocas personas que usan PyTorch. Todavía es necesario escribir un artículo. El resultado final es usar el precio de apertura, precio de cierre, precio más alto, precio de negociación más bajo y volumen de cierre de Bitcoin para predecir el próximo precio. Este tutorial ha sido producido por la plataforma FMZ Quant Trading (www.fmz.comBienvenido a unirse al grupo QQ: 863946592 para la comunicación.
2. Datos y referencias
Datos de precios de Bitcoin provenientes de la plataforma de comercio de FMZ Quant:https://www.quantinfo.com/Tools/View/4.html- ¿ Qué? Un ejemplo relacionado de predicción de precios:https://yq.aliyun.com/articles/538484¿ Qué pasa? Una introducción detallada al modelo RNN:https://zhuanlan.zhihu.com/p/27485750¿ Qué pasa? Comprensión de las entradas y salidas del RNN:https://www.zhihu.com/question/41949741/answer/318771336- ¿ Qué? Acerca de pytorch: la documentación oficial:https://pytorch.org/docsPara obtener otra información, puede buscar por sí mismo. Además, necesitas algún conocimiento previo para leer este artículo, como pandas/python/procesamiento de datos, pero no importa si no lo tienes.
3. Parámetros del modelo LSTM de la pytorch
Parámetros del LSTM:
La primera vez que vi estos parámetros densos en el documento, mi reacción fue: ¿Qué diablos es esto?
Mientras leía despacio, finalmente entendí.

input_size: Ingrese el tamaño característico del vector x. Si el precio de cierre se predice por el precio de cierre, entonces input_size=1; Si el precio de cierre se predice por alta apertura y baja cierre, entonces input_size=4.hidden_size: Tamaño implícito de la capanum_layers: Número de capas de RNN.batch_first: Si es cierto, la primera dimensión de entrada es batch_size, que también es muy confuso, y se describirá en detalle a continuación.
Introduzca los parámetros de los datos:
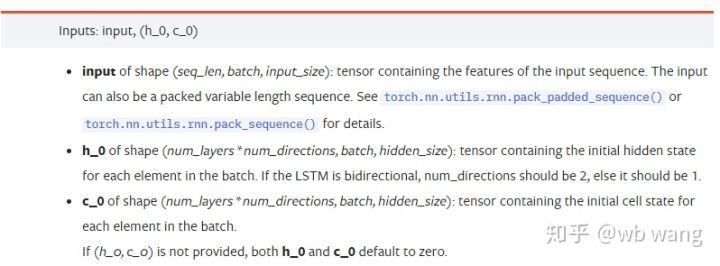
input: Los datos de entrada específicos son un tensor tridimensional, y la forma específica es: (seq_len, batch, input_size). Donde, seq_len se refiere a la longitud de la secuencia, es decir, cuánto tiempo necesita el LSTM para considerar los datos históricos. Tenga en cuenta que esto se refiere solo al formato de los datos, no a la estructura interna del LSTM. El mismo modelo LSTM puede ingresar diferentes datos de seqs_lenh_0: estado oculto inicial, forma como (num_layers * num_directions, batch, hidden_size), si se trata de una red bidireccional, num_directions=2.c_0: El estado inicial de la célula, con la forma anterior, puede no especificarse.
Parámetros de salida:
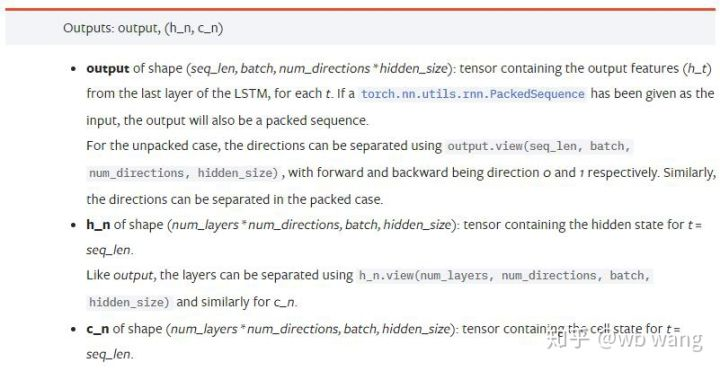
output: La forma de la salida (seq_len, batch, num_directions * hidden_size), tenga en cuenta que está relacionado con el parámetro modelo batch_first.h_n: El estado h en el momento de t = seq_len, la misma forma que h_0.c_n: El estado c en el momento de t = seq_len, la misma forma que c_0.
4. Un ejemplo simple de entrada y salida LSTM
Importar el paquete requerido primero
import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
Definir el modelo LSTM
LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)
Preparar los datos de entrada
x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657, 1.4398, -0.3479, 0.2685, 1.6903],
[ 1.0738, 0.6283, -1.3682, -0.1002, -1.7200],
[ 0.2836, 0.3013, -0.3373, -0.3271, 0.0375],
[-0.8852, 1.8098, -1.7099, -0.5992, -0.1143]],
[[ 0.6970, 0.6124, -0.1679, 0.8537, -0.1116],
[ 0.1997, -0.1041, -0.4871, 0.8724, 1.2750],
[ 1.9647, -0.3489, 0.7340, 1.3713, 0.3762],
[ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],
[[-0.5309, 0.1540, -0.4613, -0.6425, -0.1957],
[-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
[-0.4453, 0.1987, -1.0775, 1.3212, 1.3577],
[-0.5488, 0.6669, -0.2151, 0.9337, -1.1805]]])
La forma de x es (3,4,5), porque hemos definidobatch_first=TrueAnteriormente, el tamaño de batch_size en este momento es 3, sqe_len es 4, input_size es 5. X [0] representa el primer lote.
Si batch_first no está definido, el valor predeterminado es Falso, entonces la representación de datos es completamente diferente en este momento. El tamaño del lote es 4, sqe_len es 3, input_size es 5. En este momento, x [0] representa los datos de todos los lotes cuando t = 0, y así sucesivamente. Siento que esta configuración no es intuitiva, así que añadí el parámetrobatch_first=True.
La conversión de datos entre los dos también es muy conveniente:x.permute (1,0,2)
Entrada y salida
La forma de entrada y salida de LSTM es muy confusa, y la siguiente figura puede ayudarnos a entender:
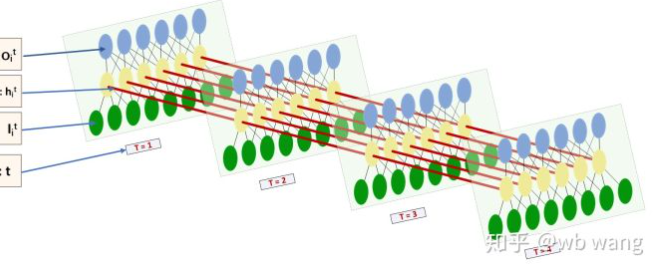
Desde:https://www.zhihu.com/question/41949741/answer/318771336.
x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])
Observe el resultado de salida, que es consistente con la interpretación del parámetro anterior. Tenga en cuenta que el segundo valor de hn.size() es 3, que es consistente con el tamaño de batch_size, lo que significa que el estado intermedio no se guarda en hn, solo se guarda el último paso. Dado que nuestra red LSTM tiene dos capas, de hecho la salida de la última capa de hn es el valor de salida. La forma de salida es [3, 4, 10], que guarda los resultados en todos los momentos de t = 0,1,2,3, por lo que:
hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]
5. Prepare los datos del mercado de Bitcoin
Mucho se ha dicho antes, que es sólo un preludio. Es muy importante entender la entrada y salida de LSTM. De lo contrario, es fácil cometer errores al extraer aleatoriamente algunos códigos de Internet. Debido a la fuerte capacidad de LSTM en series temporales, incluso si el modelo está equivocado, se pueden obtener buenos resultados al final.
Adquisición de datos
Se utilizan los datos de mercado del par de operaciones BTC_USD en Bitfinex Exchange.
import requests
import json
resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))
El formato de los datos es el siguiente:
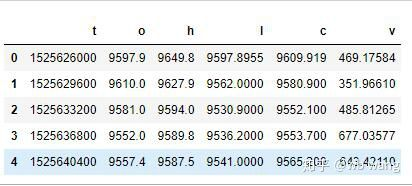
Preprocesamiento de datos
df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.
El método de estandarización de datos es muy áspero, y habrá algunos problemas.
Preparación de los datos de formación
seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
dataX, dataY=[], []
for i in range(0,len(data)-seq_len, seq_len):
dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
dataY.append(data['n'][i:i+seq_len].values)
return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))
Las formas finales de train_x y train_y son: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). Debido a que nuestro modelo predice el precio de cierre del próximo período basado en los datos de 10 períodos, hay 800 lotes en teoría, siempre y cuando haya 800 precios de cierre previstos. Pero train_y en cada lote tiene 10 datos. De hecho, el resultado intermedio de cada predicción de lote está reservado. Al calcular la pérdida final, todos los 10 resultados de predicción se pueden tomar en cuenta y comparar con el valor real en train_y. Teóricamente, solo podemos calcular la pérdida del resultado de la última predicción. Debido a que el modelo LSTM no contiene el parámetro seq_lenful en realidad, el modelo puede aplicarse a diferentes longitudes, y los resultados de predicción en el medio también son significativos, por lo que prefiero combinar y calcular pérdida.
Tenga en cuenta que cuando se preparan los datos de entrenamiento, el movimiento de la ventana está saltando, y los datos ya utilizados ya no se utilizan. Por supuesto, la ventana también se puede mover uno por uno, por lo que el conjunto de entrenamiento obtenido es mucho más grande. Sin embargo, sentí que los datos de lotes adyacentes eran demasiado repetitivos, por lo que adopté el método actual.
6. Construir el modelo LSTM
El modelo final está construido como sigue, conteniendo una capa LSTM de dos capas y una capa lineal.
class LSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
super(LSTM, self).__init__()
self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.
def forward(self, x):
x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
x = self.reg(x)
return x
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.
7. Comience a entrenar al modelo
Finalmente comenzamos el entrenamiento, el código es el siguiente:
criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
loss = criterion(out, train_y)
optimizer.zero_grad()
loss.backward() # Reverse propagation losses
optimizer.step() # Update parameters
print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))
Los resultados de la formación son los siguientes:
8. Evaluación del modelo
El valor previsto del modelo:
p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()
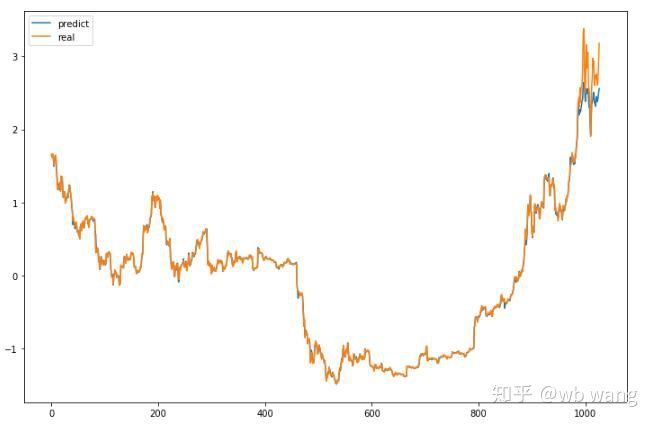
Se puede ver en el gráfico que los datos de entrenamiento (antes de 800) son muy consistentes, pero el precio de Bitcoin ha aumentado en el período posterior. Aunque el precio predicho puede no ser preciso, ¿cuál es la precisión de la predicción del aumento y la disminución?
r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))
Como resultado, el índice de precisión de las previsiones de alza y baja alcanzó el 81,4%, lo que superó aún mis expectativas.
Por supuesto, este modelo no es aplicable al bot real, pero es simple y fácil de entender.
- Introducción al arbitraje de lead-lag en criptomonedas (2)
- Introducción al conjunto de Lead-Lag en las monedas digitales (2)
- Discusión sobre la recepción de señales externas de la plataforma FMZ: una solución completa para recibir señales con servicio HTTP incorporado en la estrategia
- Exploración de la recepción de señales externas de la plataforma FMZ: estrategias para una solución completa de recepción de señales de servicios HTTP integrados
- Introducción al arbitraje de lead-lag en criptomonedas (1)
- Introducción al conjunto de Lead-Lag en las monedas digitales (1)
- Discusión sobre la recepción de señales externas de la plataforma FMZ: API extendida VS estrategia Servicio HTTP incorporado
- Exploración de la recepción de señales externas de la plataforma FMZ: API de expansión vs estrategia de servicio HTTP incorporado
- Discusión sobre el método de prueba de estrategias basado en el generador de tickers aleatorios
- Explorar métodos de prueba de estrategias basados en generadores de mercado aleatorios
- Nueva característica de FMZ Quant: Utilice la función _Serve para crear servicios HTTP fácilmente
- Sistema de negociación intradiario en punto de convergencia
- 6 estrategias y prácticas simples para principiantes en el comercio cuantitativo de moneda digital
- Marco estratégico del intervalo verdadero medio
- Práctica y aplicación de la estrategia del termostato en la plataforma FMZ Quant
- Estrategia de negociación basada en la teoría de la caja, apoyando futuros de materias primas y moneda digital
- Estrategia de negociación cuantitativa basada en el precio
- Estrategia cuantitativa de negociación utilizando un índice ponderado por volumen de negociación
- Implementación y aplicación de la estrategia de negociación PBX en la plataforma de negociación FMZ Quant
- Compartición tardía: Robot de alta frecuencia Bitcoin con 5% de rendimientos diarios en 2014
- Redes neuronales y moneda digital Serie de comercio cuantitativo (2) - Aprendizaje y capacitación intensivos Estrategia de comercio de Bitcoin
- Aplicación de la estrategia combinada del índice de resistencia relativa de la SMA y del RSI
- El desarrollo de la estrategia de CTA y la biblioteca de clases estándar de la plataforma FMZ Quant
- Estrategia de negociación cuantitativa con análisis de impulso de precios en Python
- Implementar una estrategia de negociación cuantitativa de moneda digital de doble impulso en Python
- La mejor manera de instalar y actualizar para Linux docker
- Lograr estrategias equitativas equilibradas de posiciones largas y cortas con una alineación ordenada
- Análisis de datos de series temporales y pruebas de retroceso de datos de tick
- Análisis cuantitativo del mercado de divisas digitales
- Comercio de pares basado en tecnología basada en datos
- Aplicación de la tecnología de aprendizaje automático en el comercio