Réseaux neuronaux et série de négociation quantitative de monnaie numérique (1) - LSTM prédit le prix du Bitcoin

Réseaux neuronaux et série de négociation quantitative de monnaie numérique (1) - LSTM prédit le prix du Bitcoin

1. Une brève introduction

Le réseau neuronal profond est devenu de plus en plus populaire ces dernières années. Il a résolu les problèmes qui ne pouvaient pas être résolus dans le passé dans de nombreux domaines et a démontré sa forte capacité. Dans la prédiction des séries chronologiques, le prix du réseau neuronal couramment utilisé est le RNN, car il a non seulement une entrée de données actuelle, mais aussi une entrée de données historique. Bien sûr, lorsque nous parlons de prédiction de prix RNN, nous parlons souvent de l'un des RNN: LSTM. Cet article construira un modèle pour prédire le prix du Bitcoin basé sur PyTorch. Bien qu'il existe beaucoup d'informations pertinentes sur Internet, il n'est toujours pas suffisamment complet, et il y a encore relativement peu de gens qui utilisent PyTorch. Il est nécessaire d'écrire un article final. Le résultat final est d'utiliser le prix d'ouverture, le prix de clôture, le prix le plus bas, le prix de négociation le plus bas et le volume de clôture du Bitcoin pour prédire le Ce tutoriel est produit par la plateforme FMZ Quant Trading (www.fmz.comBienvenue dans le groupe QQ: 863946592 pour la communication.

2. Données et référence

Les données sur le prix du Bitcoin proviennent de la plateforme de trading FMZ Quant:https://www.quantinfo.com/Tools/View/4.htmlJe suis désolée. Un exemple connexe de prévision des prix:https://yq.aliyun.com/articles/538484Je suis désolée. Une introduction détaillée au modèle RNN:https://zhuanlan.zhihu.com/p/27485750Je suis désolée. Comprendre l'entrée et la sortie du RNN:https://www.zhihu.com/question/41949741/answer/318771336Je suis désolée. À propos de pytorch: la documentation officielle:https://pytorch.org/docsPour d'autres informations, vous pouvez chercher par vous-même. En outre, vous avez besoin de connaissances préalables pour lire cet article, telles que les pandas/python/traitement de données, mais cela n'a pas d'importance si vous ne le faites pas.

Paramètres du modèle LSTM pytorch

Paramètres du LSTM:

La première fois que j'ai vu ces paramètres denses sur le document, ma réaction a été:

En lisant lentement, j'ai finalement compris.

input_sizeSi le prix de clôture est prédit par le prix de clôture, alors input_size=1; Si le prix de clôture est prédit par un prix d'ouverture élevé et un prix de clôture bas, alors input_size=4.hidden_size: Taille implicite de la couchenum_layers: Nombre de couches de RNN.batch_first: Si c'est vrai, la première dimension d'entrée est batch_size, ce qui est également très déroutant et sera décrit en détail ci-dessous.

Entrez les paramètres de données:

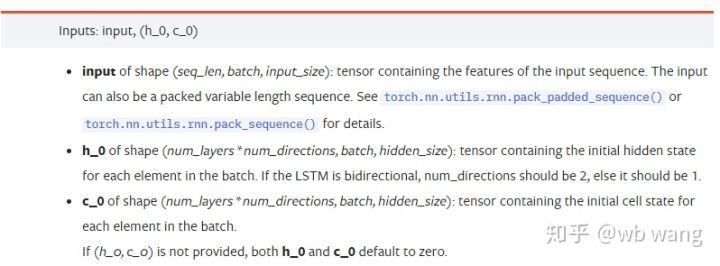
input: Les données d'entrée spécifiques sont un tenseur tridimensionnel, et la forme spécifique est: (seq_len, batch, input_size). Où, seq_len fait référence à la longueur de la séquence, c'est-à-dire à la durée dont le LSTM a besoin pour considérer les données historiques. Notez que cela se réfère uniquement au format des données, pas à la structure interne du LSTM. Le même modèle LSTM peut entrer différentes données seqs_lens, ce qui peut donner des résultats de prédiction; batch fait référence à la taille du lot, représentant le nombre de groupes de données différents; input_size est la taille d'entrée précédente.h_0: État caché initial, forme comme (num_layer * num_directions, lot, hidden_size), s'il s'agit d'un réseau bidirectionnel, num_directions=2.c_0: L'état initial de la cellule, la forme comme ci-dessus, peut ne pas être spécifié.

Paramètres de sortie:

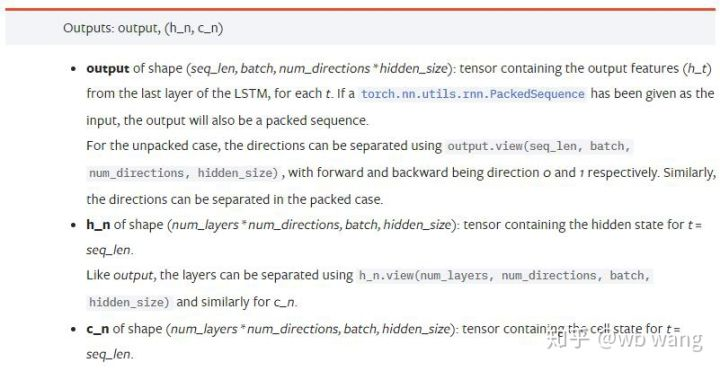
output: La forme de la sortie (seq_len, batch, num_directions * hidden_size), notez qu'elle est liée au paramètre de modèle batch_first.h_n: L'état h au moment de t = seq_len, même forme que h_0.c_n: L'état c au moment de t = seq_len, même forme que c_0.

4. Un exemple simple d'entrée et de sortie LSTM

Importez d'abord le paquet requis

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Définir le modèle LSTM

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Préparez les données d'entrée

x = torch.randn(3,4,5)
# The value of x is:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

La forme de x est (3,4,5), parce que nous avons définibatch_first=Trueprécédemment, la taille de batch_size à ce moment est 3, sqe_len est 4, input_size est 5. X [0] représente le premier lot.

Si batch_first n'est pas défini, la valeur par défaut est False, alors la représentation des données est complètement différente à ce moment-là. La taille du lot est 4, sqe_len est 3, input_size est 5. À ce moment-là, x [0] représente les données de tous les lots lorsque t = 0, et ainsi de suite. Je pense que ce paramètre n'est pas intuitif, alors j'ai ajouté le paramètrebatch_first=True.

La conversion des données entre les deux est également très pratique:x.permute (1,0,2)

Entrée et sortie

La forme de l'entrée et de la sortie de LSTM est très déroutante, et la figure suivante peut nous aider à comprendre:

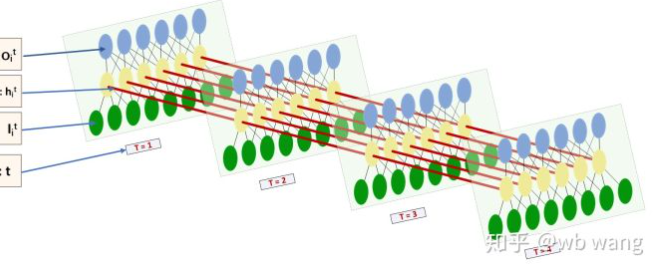
De:https://www.zhihu.com/question/41949741/answer/318771336.

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) # Thinking about it, what would be the size of the output if batch_first=False?
print(hn.size())
print(cn.size())
# result
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Observez le résultat de sortie, qui est conforme à l'interprétation du paramètre précédent. Notez que la deuxième valeur de hn.size() est 3, ce qui est conforme à la taille de batch_size, ce qui signifie que l'état intermédiaire n'est pas enregistré dans hn, seule la dernière étape est enregistrée. Puisque notre réseau LSTM a deux couches, en fait, la sortie de la dernière couche de hn est la valeur de sortie.

hn[-1][0] == output[0][-1] # The output of the first batch at the last level of hn is equal to the output of the first batch at t=3.
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Préparez les données du marché Bitcoin

Il est très important de comprendre l'entrée et la sortie de LSTM. Sinon, il est facile de faire des erreurs en extraisant aléatoirement certains codes d'Internet. En raison de la forte capacité de LSTM dans les séries temporelles, même si le modèle est faux, de bons résultats peuvent être obtenus à la fin.

Acquisition de données

Les données de marché de la paire de transactions BTC_USD dans Bitfinex Exchange sont utilisées.

import requests
import json

resp = requests.get('https://www.quantinfo.com/API/m/chart/history?symbol=BTC_USD_BITFINEX&resolution=60&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

Le format des données est le suivant:

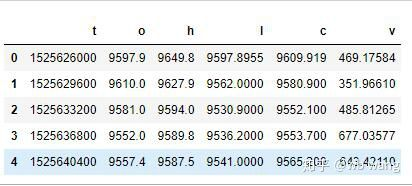
Pré-traitement des données

df.index = df['t'] # index is set to timestamp
df = (df-df.mean())/df.std() # The standardization of the data, otherwise the loss of the model will be very large, which is not conducive to convergence.
df['n'] = df['c'].shift(-1) # n is the closing price of the next period, which is our forecast target.
df = df.dropna()
df = df.astype(np.float32) # Change the data format to fit pytorch.

La méthode de normalisation des données est très grossière, et il y aura quelques problèmes.

Préparer les données de formation

seq_len = 10 # Input 10 periods of data
train_size = 800 # Training set batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) # The change in shape, -1 represents the value that will be calculated automatically.
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

Les formes finales de train_x et train_y sont: torch.Size ([800, 10, 5]), torch.Size ([800, 10, 1]). Comme notre modèle prédit le prix de clôture de la période suivante sur la base des données de 10 périodes, il y a en théorie 800 lots, tant qu'il y a 800 prix de clôture prédits. Mais train_y dans chaque lot a 10 données. En fait, le résultat intermédiaire de chaque prédiction de lot est réservé. Lors du calcul de la perte finale, tous les 10 résultats de prédiction peuvent être pris en compte et comparés à la valeur réelle en train_y. Théoriquement, nous pouvons calculer la Perte du seul résultat de la dernière prédiction. Parce que le modèle LSTM ne contient pas de paramètre seq_lenful en réalité, le modèle peut donc être appliqué à différentes longueurs, et les résultats de prédiction au milieu sont également significatifs, donc je préfère combiner et calculer la Perte.

Notez que lors de la préparation des données d'entraînement, le mouvement de la fenêtre est sautant, et les données déjà utilisées ne sont plus utilisées. Bien sûr, la fenêtre peut également être déplacée une par une, de sorte que l'ensemble d'entraînement obtenu est beaucoup plus grand. Cependant, j'ai estimé que les données de lot adjacentes étaient trop répétitives, alors j'ai adopté la méthode actuelle.

6. Construire le modèle LSTM

Le modèle final est construit comme suit, contenant une LSTM à deux couches et une couche linéaire.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # Linear layer, output the result of LSTM into a value.

    def forward(self, x):
        x, _ = self.rnn(x) # If you don't understand the change of data dimension in forward propagation, you can debug it separately.
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size is 5, which represents the high opening and low closing and trading volume. The implicit layer is 10.

7. Commencez à former le modèle

Enfin, nous commençons l'entraînement, le code est le suivant:

criterion = nn.MSELoss() # A simple mean square error loss function is used.
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # Optimize function, lr is adjustable.
for epoch in range(600): # Because of the speed, there are more epochs here.
    out = net(train_x) # Due to the small amount of data, the full amount of data is directly used for calculation.
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # Reverse propagation losses
    optimizer.step() # Update parameters
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Les résultats de la formation sont les suivants:

8. Évaluation du modèle

La valeur prévue du modèle:

p = net(torch.from_numpy(data_X))[:,-1,0] # Only the last predicted value is taken here for comparison.
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

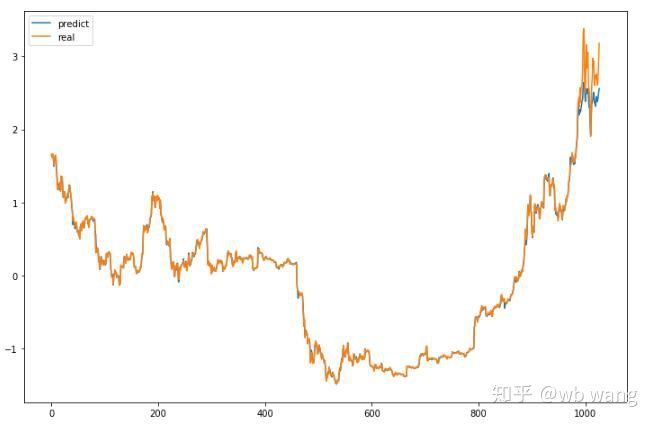
On peut voir sur le graphique que les données de formation (avant 800) sont très cohérentes, mais le prix du Bitcoin a augmenté dans la période ultérieure. Le modèle n'a pas vu ces données, de sorte que la prédiction est inadéquate. Cela montre également qu'il y a des problèmes dans la normalisation des données. Bien que le prix prédit ne soit pas précis, quelle est l'exactitude de la prédiction de l'augmentation et de la diminution? Prenez un segment de données de prévision pour voir:

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

En conséquence, le taux de précision des prévisions de hausse et de baisse a atteint 81,4%, ce qui dépasse encore mes attentes.

Bien sûr, ce modèle ne s'applique pas au vrai bot, mais il est simple et facile à comprendre.